Kreuzprodukt / Vektorprodukt
Hier erklären wir dir, wie du das Kreuzprodukt oder Vektorprodukt zweier Vektoren berechnest. Du möchtest das Kreuzprodukt in kürzester Zeit berechnen können? Dann schau dir unser Video
dazu an!
Inhaltsübersicht
Kreuzprodukt einfach erklärt
Das Kreuzprodukt (oder Vektorprodukt) liefert dir im Gegensatz zum Skalarprodukt als Ergebnis einen Vektor. Dieser Vektor steht senkrecht (orthogonal
) zu deinen beiden anderen Vektoren. Du kannst ihn auch Normalenvektor nennen.
Die Formel des Kreuzprodukts der Vektoren 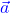 und
und  lautet:
lautet:
![Rendered by QuickLaTeX.com \[\textcolor{blue}{\vec{a}} \times \textcolor{teal}{\vec{b}} = \left(\begin{array}{c} \textcolor{blue}{a_1} \\ \textcolor{blue}{a_2} \\ \textcolor{blue}{a_3}\end{array}\right) \times \left(\begin{array}{c} \textcolor{teal}{b_1} \\ \textcolor{teal}{b_2} \\ \textcolor{teal}{b_3}\end{array}\right) = \left(\begin{array}{c} \textcolor{blue}{a_2}\textcolor{teal}{b_3} - \textcolor{blue}{a_3}\textcolor{teal}{b_2} \\ \textcolor{blue}{a_3}\textcolor{teal}{b_1} - \textcolor{blue}{a_1}\textcolor{teal}{b_3} \\ \textcolor{blue}{a_1}\textcolor{teal}{b_2} - \textcolor{blue}{a_2}\textcolor{teal}{b_1} \end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fbc3a943ff1e2510d67ac12f984eaf3d_l3.png)
Beispiel: Das Kreuzprodukt der Vektoren 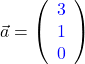 und
und  berechnest du so:
berechnest du so:
![Rendered by QuickLaTeX.com \[\textcolor{blue} {\vec{a}} \times \textcolor{teal} {\vec{b}} = \left(\begin{array}{c} \textcolor{blue}{1} \cdot \textcolor{teal}{0} - \textcolor{blue}{0} \cdot \textcolor{teal}{1} \\ \textcolor{blue}{0} \cdot\textcolor{teal}{(-1)} - \textcolor{blue}{3} \cdot \textcolor{teal}{0} \\ \textcolor{blue}{3} \cdot \textcolor{teal}{1} - \textcolor{blue}{1} \cdot \textcolor{teal}{(-1)} \end{array}\right) = \left(\begin{array}{c} \textcolor{red}{0} \\ \textcolor{red}{0} \\ \textcolor{red}{4}\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-65a093d5c9521ec4eb48d0e066a0a8bc_l3.png)
Wichtig: Der Betrag des Kreuzprodukts  (also die Länge des Normalenvektors kannst du auch so bestimmen:
(also die Länge des Normalenvektors kannst du auch so bestimmen:
![Rendered by QuickLaTeX.com \[|\textcolor{red}{\vec{a} \times\vec{b}}| = |\textcolor{blue}{\vec{a}}| \cdot |\textcolor{teal}{\vec{b}}| \cdot \sin{\varphi}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-96be9f4542459cd5f4474da51d070af8_l3.png)
Außerdem gibt  den Flächeninhalt des von
den Flächeninhalt des von  und
und  aufgespannten Parallelogramms an.
aufgespannten Parallelogramms an.
Kreuzprodukt berechnen
Es gibt eine Methode, das Kreuzprodukt zweier Vektoren  und
und  zu berechnen, ohne die Formel auswendig lernen zu müssen. Dabei gehst du wie folgt vor:
zu berechnen, ohne die Formel auswendig lernen zu müssen. Dabei gehst du wie folgt vor:
Schreibe das Kreuzprodukt der beiden Vektoren auf und schreibe die ersten zwei Zeilen nochmal unter die Vektoren.

Nun bestimmst du nach und nach die einzelnen Komponenten des Vektorprodukts. Für die erste Komponente bildest du das Produkt
 und ziehst davon
und ziehst davon 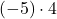 ab.
ab.
 .
.
Für den zweiten Wert des Vektorprodukts verschiebst du die Rechnung um eins nach unten.
Das heißt, du rechnest 
 .
.
Verschiebe die Rechnung noch einmal nach unten, um den dritten Wert des Vektorprodukts zu bestimmen.
Du bestimmst also das Produkt  und subtrahierst
und subtrahierst  . Damit erhältst du dann die dritte Komponente vom Kreuzprodukt.
. Damit erhältst du dann die dritte Komponente vom Kreuzprodukt.
 .
.
Also ist das Vektorprodukt der Vektoren  und
und  gegeben durch
gegeben durch
 .
.
Du kannst dir für die Rechnung folgendes merken:
Für die Komponente eines Kreuzprodukts gilt: Links oben mal rechts unten minus links unten mal rechts oben.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel: Vektorprodukt
Betrachte die zwei Vektoren  und
und  . Um das Kreuzprodukt mit der Formel zu berechnen, gehst du so vor:
. Um das Kreuzprodukt mit der Formel zu berechnen, gehst du so vor:

und erhältst somit für das Vektorprodukt die Lösung
 .
.
Kreuzprodukt Eigenschaften
Im Folgenden Abschnitt zeigen wir dir ein paar Eigenschaften des Kreuzprodukts/Vektorprodukts.
- Das Vektorprodukt ist nicht kommutativ, bei der Berechnung spielt die Reihenfolge also eine Rolle. Wenn du die beiden Vektoren vertauschst, erhältst du als Vektorprodukt den Gegenvektor
![Rendered by QuickLaTeX.com \[\vec{a} \times \vec{b} = - (\vec{b} \times \vec{a})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c94594c3422b431baef88e64fdefe97d_l3.png)
- Das Vektorprodukt ist nicht assoziativ.
- Es gilt das Distributivgesetz:
![Rendered by QuickLaTeX.com \[\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-23fbe8292e94c42117792051c09ff336_l3.png)
- Außerdem gilt die Regel:
![Rendered by QuickLaTeX.com \[(r \cdot \vec{a}) \times \vec{b} = r \cdot (\vec{a} \times \vec{b}) = \vec{a} \times (r \cdot \vec{b})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f2bb485da016051dc199da0217548909_l3.png)
Senkrechte Vektoren bestimmen
Wenn du zwei Vektoren gegeben hast und einen weiteren Vektor suchst, der auf beiden Vektoren senkrecht
steht, so hilft dir das Berechnen des Kreuzprodukt (Vektorprodukt) weiter, denn das Kreuzprodukt zweier Vektoren  und
und  steht sowohl senkrecht auf
steht sowohl senkrecht auf  , als auch auf
, als auch auf  . Somit sind auch alle skalaren Vielfache vom Kreuzprodukt
. Somit sind auch alle skalaren Vielfache vom Kreuzprodukt  Vektoren, die senkrecht auf
Vektoren, die senkrecht auf  und
und  stehen.
stehen.
Betrag Kreuzprodukt
Der Betrag des Kreuzprodukts von  und
und  entspricht der Fläche des Parallelogramms, das von den beiden Vektoren aufgespannt wird.
entspricht der Fläche des Parallelogramms, das von den beiden Vektoren aufgespannt wird.
So ist zum Beispiel der Flächeninhalt des Parallelogramms, das von den zwei Vektoren  und
und  aufgespannt wird, gegeben durch
aufgespannt wird, gegeben durch


Das Volumen eines Spats
Für einen beliebigen Vektor  spannen die Vektoren
spannen die Vektoren  ,
,  und
und  einen Spat auf. Dabei bezeichnest du die Formel
einen Spat auf. Dabei bezeichnest du die Formel  als das Spatprodukt und der Betrag des Spatprodukts
als das Spatprodukt und der Betrag des Spatprodukts
 entspricht dem Volumen des Spats.
entspricht dem Volumen des Spats.
Betrachtest du nochmal die Vektoren  und
und  aus dem ersten Beispiel und den Vektor
aus dem ersten Beispiel und den Vektor  , so lautet das Spatprodukt mit
, so lautet das Spatprodukt mit 

Der Betrag des Spatprodukts  entspricht dem Volumen des Spats.
entspricht dem Volumen des Spats.
Weitere Themen der Vektorrechnung
Neben dem Kreuzprodukt und Vektorprodukt gibt es noch weitere Themen, die sich mit Vektoren beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:
- Vektor
- Betrag eines Vektors
- Linearkombination
- Winkel zwischen zwei Vektoren
- Einheitsvektor
- Skalarprodukt
- Spatprodukt
Vektorprodukt Aufgaben
Im Folgenden Abschnitt geben wir dir zwei Aufgaben mit Lösungen, um das Kreuzprodukt/Vektorprodukt üben zu können.
Aufgabe 1: Kreuzprodukt berechnen
Berechne mit der Formel das Kreuzprodukt/Vektorprodukt der beiden Vektoren  und
und 
Lösung Aufgabe 1
Um das Kreuzprodukt zu berechnen, verwendest du die Formel
 .
.
Setze also die Komponenten der beiden Vektoren in die Formel ein, um so das Kreuzprodukt zu berechnen
 .
.
Aufgabe 2: Vektorprodukt anwenden
Berechne den Flächeninhalt  des Dreiecks
mit den Eckpunkten
des Dreiecks
mit den Eckpunkten  ,
,  und
und  . Verwende dazu das Vektorprodukt.
. Verwende dazu das Vektorprodukt.
Lösung Aufgabe 2
Du benötigst zuerst die zwei Vektoren  und
und  , die das Dreieck aufspannen. Du rechnest also
, die das Dreieck aufspannen. Du rechnest also

 .
.
Als nächstes brauchst du das Vektorprodukt der beiden Vektoren  und
und  . Um das Kreuzprodukt mit der Formel zu berechnen, gehst du so vor:
. Um das Kreuzprodukt mit der Formel zu berechnen, gehst du so vor:

Nun berechnest du den Betrag des Kreuzprodukts. Damit hast du dann mit

den Flächeninhalt des Parallelogramms, das von den beiden Vektoren aufgespannt wird. Da das Dreieck nur halb so groß ist wie das Parallelogramm, halbierst du das Ergebnis. Somit hast du mit

den Flächeninhalt des Dreiecks berechnet.
Kreuzprodukt / Vektorprodukt — häufigste Fragen
-
Was ist das Kreuzprodukt bei Vektoren?
Das Kreuzprodukt bei Vektoren ist das miteinander Malnehmen (Multiplizieren) zweier Vektoren. Als Ergebnis bekommst du einen Vektor, der senkrecht auf den beiden anderen Vektoren steht. Ihn nennst du auch Normalenvektor.
-
Wie lautet die Formel für das Kreuzprodukt?
Die Formel für das Kreuzprodukt lautet: a → * b → = – (b → * a →)
Durch das Tauschen von a und b erhältst du den Gegenvektor. Hier muss das Vorzeichen wechseln, damit der neue Vektor in die andere Richtung zeigt.
Skalarprodukt
Super, jetzt kannst du das Vektorprodukt / Kreuzprodukt mithilfe der Formel berechnen! Das Vektorprodukt liefert dir immer einen senkrechten Vektor zu deinen zwei gegebenen Vektoren. Um zu überprüfen, ob zwei Vektoren wirklich senkrecht zueinander stehen, kannst du das Skalarprodukt nutzen. Schau dir doch einfach unser Video dazu an!






