Video

Quiz

Einheitsmatrix

Du fragst dich, was eine Einheitsmatrix ist und welche Eigenschaften sie hat? Das erfährst du hier.

Inhaltsübersicht

Einheitsmatrix — einfach erklärt

Eine Einheitsmatrix ist eine quadratische Matrix, bei der nur die Hauptdiagonale aus Einsen besteht. Alle anderen Elemente in der Matrix sind null.

Die Hauptdiagonale geht dabei von links oben nach rechts unten. Da eine Einheitsmatrix quadratisch ist, hat sie genauso viele Zeilen wie Spalten, also zum Beispiel 2 x 2 oder 3 x 3.

Eine Einheitsmatrix kannst du auch Identitätsmatrix nennen. Daher verwendest du als Bezeichnung für eine Einheitsmatrix entweder E für Einheitsmatrix oder I für Identitätsmatrix. Zusätzlich kann ein Index angeben, welche Größe die Matrix hat. Zum Beispiel kannst du eine 2 x 2 Einheitsmatrix mit E_2 bezeichnen.

So sieht eine 2×2 Einheitsmatrix aus:

$E_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

Übrigens: Die Dimension gibt an, wie viele Zeilen und Spalten die Matrix hat. Sie wird in der Form m x n angegeben, wobei $die Anzahl der Zeilen und die Anzahl der Spalten ist.$

Eigenschaften einer Einheitsmatrix

Eine Einheitsmatrix hat mehrere besondere Eigenschaften:

neutrales Element in der Matrixmultiplikation
invers zu sich selbst
einzigartig
transponierbar
Spur entspricht der Anzahl der Zeilen (oder Spalten) der Matrix
Determinante ist 1

Neutrales Element in der Matrixmultiplikation

Die Einheitsmatrix funktioniert in der Matrixmultiplikation wie die Zahl 1 bei der normalen Multiplikation. Multiplizierst du eine Matrix A mit der Einheitsmatrix, kommt wieder die ursprüngliche Matrix A heraus. Sie ist in der Rechnung also neutral und verändert die ursprüngliche Matrix nicht.

$A \cdot E = A$ , $E \cdot A = A$

Beispiel:

Matrix mal Einheitsmatrix: $A \cdot E = A$

$A = \begin{pmatrix} \textcolor{red}2 & \textcolor{red}3 \\ \textcolor{orange}4 & \textcolor{orange} 5 \end{pmatrix}$ $E_2= \begin{pmatrix} \textcolor{blue}1 &\textcolor{teal} 0 \\ \textcolor{blue}0 &\textcolor{teal} 1 \end{pmatrix}$

$\begin{pmatrix} \textcolor{red}2 & \textcolor{red}3 \\ \textcolor{orange}4 & \textcolor{orange} 5 \end{pmatrix} \cdot \begin{pmatrix} \textcolor{blue}1 &\textcolor{teal} 0 \\ \textcolor{blue}0 &\textcolor{teal} 1 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{red}2 \cdot \textcolor{blue}1 + \textcolor{red}3 \cdot \textcolor{blue}0 & \textcolor{red}2 \cdot \textcolor{teal}0 + \textcolor{red}3 \cdot \textcolor{teal}1 \\ \textcolor{orange}4 \cdot \textcolor{blue}1 + \textcolor{orange}5 \cdot \textcolor{blue}0 & \textcolor{orange}4 \cdot \textcolor{teal}0 + \textcolor{orange}5 \cdot \textcolor{teal}1 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{violet}2 & \textcolor{violet}3 \\ \textcolor{violet}4 & \textcolor{violet} 5 \end{pmatrix}$

Einheitsmatrix mal Matrix: $E \cdot A = A$

$E_2= \begin{pmatrix} \textcolor{red}1 & \textcolor{red}0 \\ \textcolor{orange}0 & \textcolor{orange} 1 \end{pmatrix}$ $A= \begin{pmatrix} \textcolor{blue}2 &\textcolor{teal} 3 \\ \textcolor{blue}4 &\textcolor{teal} 5 \end{pmatrix}$

$\begin{pmatrix} \textcolor{red}1 & \textcolor{red}0 \\ \textcolor{orange}0 & \textcolor{orange} 1 \end{pmatrix} \cdot \begin{pmatrix} \textcolor{blue}2 &\textcolor{teal} 3 \\ \textcolor{blue}4 &\textcolor{teal} 5 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{red}1 \cdot \textcolor{blue}2 + \textcolor{red}0 \cdot \textcolor{blue}4 & \textcolor{red}1 \cdot \textcolor{teal}3 + \textcolor{red}0 \cdot \textcolor{teal}5 \\ \textcolor{orange}0 \cdot \textcolor{blue}2 + \textcolor{orange}1\cdot \textcolor{blue}4 & \textcolor{orange}0 \cdot \textcolor{teal}3 + \textcolor{orange}1 \cdot \textcolor{teal}5 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{violet}2 & \textcolor{violet}3 \\ \textcolor{violet}4 & \textcolor{violet} 5 \end{pmatrix}$

Invers zu sich selbst

Multiplizierst du eine Matrix mit ihrer inversen Matrix $A^{-1}$ , erhältst du als Ergebnis die Einheitsmatrix. Das Besondere bei der Einheitsmatrix ist, dass ihre inverse Matrix $E^{-1}$ auch die Einheitsmatrix ist.

Das bedeutet, wenn du die Einheitsmatrix mit sich selbst multiplizierst, erhältst du wieder die Einheitsmatrix. Sie ist also zu sich selbst invers.

$E^{-1}$ =

Beispiel:

$E_2 = \begin{pmatrix} \textcolor{red}1 & \textcolor{red}0 \\ \textcolor{orange}0 & \textcolor{orange} 1 \end{pmatrix}$ ${E_2}^{-1} = \begin{pmatrix} \textcolor{blue}1 &\textcolor{teal} 0 \\ \textcolor{blue}0 &\textcolor{teal} 1 \end{pmatrix}$

$\begin{pmatrix} \textcolor{red}1 & \textcolor{red}0 \\ \textcolor{orange}0 & \textcolor{orange} 1 \end{pmatrix} \cdot \begin{pmatrix} \textcolor{blue}1 &\textcolor{teal} 0 \\ \textcolor{blue}0 &\textcolor{teal} 1 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{red}1 \cdot \textcolor{blue}1 + \textcolor{red}0 \cdot \textcolor{blue}0 & \textcolor{red}1 \cdot \textcolor{teal}0 + \textcolor{red}0 \cdot \textcolor{teal}1 \\ \textcolor{orange}0 \cdot \textcolor{blue}1 + \textcolor{orange}1 \cdot \textcolor{blue}0 & \textcolor{orange}0 \cdot \textcolor{teal}0 + \textcolor{orange}1 \cdot \textcolor{teal}1 \end{pmatrix}$ = $\begin{pmatrix} \textcolor{violet}1 & \textcolor{violet}0 \\ \textcolor{violet}0 & \textcolor{violet} 1 \end{pmatrix}$

Einzigartig

Es gibt für jede Größe einer quadratischen Matrix genau eine Einheitsmatrix. Sie ist also einzigartig für jede Dimension.

Beispiel:

$E_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ ist die einzige 2×2 Einheitsmatrix

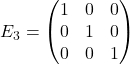$E_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ ist die einzige 3×3 Einheitsmatrix

Transponierbar

Die Einheitsmatrix ändert sich nicht, wenn du sie transponierst, also wenn du ihre Zeilen und Spalten vertauschst. Die transponierte Matrix der Einheitsmatrix ist wieder die Einheitsmatrix. Damit ist die Einheitsmatrix spiegelsymmetrisch zu ihrer Hauptdiagonalen.
$E^{T}$ =

Beispiel:

$E_2 = \begin{pmatrix} \textcolor{red}1 & \textcolor{red}0 \\ \textcolor{orange}0 & \textcolor{orange} 1 \end{pmatrix}$ ${E_2}^{T} = \begin{pmatrix} \textcolor{red}1 & \textcolor{orange}0 \\ \textcolor{red}0 & \textcolor{orange} 1 \end{pmatrix}$

Spur

Die Spur der Einheitsmatrix, also die Summe der Elemente auf der Hauptdiagonale, entspricht der Anzahl der Zeilen (oder Spalten) der Matrix. Für eine 3×3-Einheitsmatrix ist die Spur also 3.

Beispiel:

$E_3 = \begin{pmatrix} \textcolor{red}1 & 0 & 0 \\ 0 & \textcolor{red}1 &0\\0&0&\textcolor{red}1 \end{pmatrix}$ Spur (E_3) = 1 + 1 + 1 = 3

Determinante

Die Determinante der Einheitsmatrix ist immer 1. Bei einer Matrix, bei der alle Elemente unterhalb der Hauptdiagonale Null sind, ist die Determinante das Produkt der Elemente aus der Hauptdiagonale. Eine Einheitsmatrix hat in der Hauptdiagonalen nur Einsen.

det(E)=1

Beispiel:

$E_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ $det(E_2)= 1 \cdot 1 = 1$

Einheitsmatrix — häufigste Fragen

Was ist eine Identitätsmatrix?
Die Einheitsmatrix oder Identitätsmatrix ist eine quadratische Matrix, bei der nur die Hauptdiagonale aus Einsen besteht, während alle anderen Elemente in der Matrix null sind. Sie ist das neutrale Element in der Matrixmultiplikation.
Was ist die Determinante der Einheitsmatrix?
Die Determinante einer Einheitsmatrix ist immer 1, unabhängig von ihrer Größe. Dies liegt daran, dass die Multiplikation der Einsen auf der Hauptdiagonale den Wert 1 ergibt.

Determinante berechnen

Jetzt weißt du, was die Einheitsmatrix ist und welche besonderen Eigenschaften sie hat. Wenn du dir nochmal ansehen willst, wie du die Determinante einer Matrix berechnest, schau hier rein.

Zum Video: Determinante berechnen

Beliebte Inhalte aus dem Bereich Lineare Algebra

Was ist eine Matrix?

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .