Eigenvektor
In diesem Artikel behandeln wir Eigenvektoren und zeigen auf, wie man einen Eigenvektor berechnen kann. Darüber hinaus gehen wir noch auf den Eigenraum ein.
Zusätzlich zu diesem Artikel haben wir das Thema in einem Video für dich aufbereitet. So können Sachverhalte nämlich einfacher und einprägsamer dargestellt werden, was dich beim Lernen unterstützt. Schau doch mal rein!
Inhaltsübersicht
Eigenvektoren berechnen
In zwei einfachen Schritten lässt sich ein Eigenvektor berechnen. Diese sind hier zusammengefasst:
-
Eigenwerte
berechnen und in die Eigenwertgleichung einsetzen

- Gleichungssystem lösen
Diese beiden Schritte wollen wir allerdings im Folgenden noch etwas genauer erläutern.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Eigenvektor einer Matrix: Eigenwerte in Eigenwertgleichung einsetzen
In unserem Artikel und Video zu den Eigenwerten haben wir dir bereits kurz erklärt, was ein Eigenvektor einer Matrix ist.
Den Faktor, um wie viel der Vektor nach Multiplikation mir der Matrix länger oder kürzer geworden ist, nennt man Eigenwert. In einer Gleichung formuliert sieht das Ganze folgendermaßen aus:

Hier ist  eine gegebene quadratische
eine gegebene quadratische  -Matrix. Die Vektoren
-Matrix. Die Vektoren 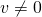 , für die diese Gleichung gilt, heißen Eigenvektoren der Matrix. Die zugehörigen Zahlen
, für die diese Gleichung gilt, heißen Eigenvektoren der Matrix. Die zugehörigen Zahlen  sind ihre Eigenwerte. Die Eigenwerte lassen sich durch ein einfaches Verfahren bestimmen, wie wir in einem Artikel und Video bereits gezeigt haben. Außerdem haben wir dort auch thematisiert, dass die Gleichung
sind ihre Eigenwerte. Die Eigenwerte lassen sich durch ein einfaches Verfahren bestimmen, wie wir in einem Artikel und Video bereits gezeigt haben. Außerdem haben wir dort auch thematisiert, dass die Gleichung  als Eigenwertproblem bzw. Eigenwertgleichung bezeichnet wird. Man kann diese Gleichung auch in folgende Form bringen:
als Eigenwertproblem bzw. Eigenwertgleichung bezeichnet wird. Man kann diese Gleichung auch in folgende Form bringen:  Hierbei ist
Hierbei ist  die
die  -Einheitsmatrix. Wenn man nun in diese Gleichung die berechneten Eigenwerte einsetzt, erhält man ein Gleichungssystem. Mithilfe dessen lassen sich Eigenvektoren berechnen.
-Einheitsmatrix. Wenn man nun in diese Gleichung die berechneten Eigenwerte einsetzt, erhält man ein Gleichungssystem. Mithilfe dessen lassen sich Eigenvektoren berechnen.
Beispiel: Eigenvektor berechnen
Nun wollen wir anhand eines Beispiels demonstrieren, wie man Eigenvektoren berechnen kann. Dazu betrachten wir die folgende Matrix
 .
.
Die Eigenwerte für diese Matrix haben wir bereits in einem anderen Artikel und Video bestimmt. Sie lauten  . Wir wollen für den doppelten Eigenwert
. Wir wollen für den doppelten Eigenwert 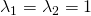 die Eigenvektoren bestimmen. Hierfür setzen wir im ersten Schritt den Eigenwert
die Eigenvektoren bestimmen. Hierfür setzen wir im ersten Schritt den Eigenwert 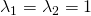 in die Eigenwertgleichung
in die Eigenwertgleichung 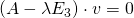 ein und erhalten:
ein und erhalten:

Die Lösungsmenge dieses Gleichungssystems sieht folgendermaßen aus:

Jeder Vektor aus dieser Lösungsmenge ist also ein Eigenvektor der Matrix  zum Eigenwert 1. Das kann man auch leicht nachkontrollieren, indem man einen Vektor der Lösungsmenge an die Matrix multipliziert. Das Ergebnis ist dann der Vektor selbst.
zum Eigenwert 1. Das kann man auch leicht nachkontrollieren, indem man einen Vektor der Lösungsmenge an die Matrix multipliziert. Das Ergebnis ist dann der Vektor selbst.
Eigenraum
In dem eben gezeigten Beispiel hat man gesehen, dass es zu einem Eigenwert nicht nur einen einzelnen Eigenvektor gibt. Vereinigt man alle Eigenvektoren eines Eigenwertes  mit dem Nullvektor, so erhält man einen Untervektorraum des
mit dem Nullvektor, so erhält man einen Untervektorraum des  . Diesen Untervektorraum nennt man den Eigenraum zum Eigenwert
. Diesen Untervektorraum nennt man den Eigenraum zum Eigenwert  .
.
Algebraische und geometrische Vielfachheit
Die Dimension des Eigenraums wird als geometrische Vielfachheit des Eigenwertes  bezeichnet. Sie wird unterschieden von der algebraischen Vielfachheit. Diese ist die Vielfachheit des Eigenwertes als Nullstelle des charakteristischen Polynoms
.
bezeichnet. Sie wird unterschieden von der algebraischen Vielfachheit. Diese ist die Vielfachheit des Eigenwertes als Nullstelle des charakteristischen Polynoms
.
Beispiel: Eigenwerte und Eigenvektoren berechnen
Nun wollen wir in einem Beispiel noch einmal komplett aufzeigen, wie man für eine gegebene Matrix die Eigenwerte und Eigenvektoren berechnen kann. Dazu betrachten wir die Matrix
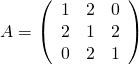 .
.
Wir bestimmen zunächst das charakteristische Polynom  , indem wir die Determinante der Matrix
, indem wir die Determinante der Matrix  ermitteln:
ermitteln:

Die Nullstellen dieses Polynoms und somit die Eigenwerte der Matrix sind  und
und  . Wir wollen zunächst für den Eigenwert
. Wir wollen zunächst für den Eigenwert  einen Eigenvektor berechnen. Dazu setzen wir den Eigenwert in die Gleichung
einen Eigenvektor berechnen. Dazu setzen wir den Eigenwert in die Gleichung  ein und erhalten folgenden Ausdruck:
ein und erhalten folgenden Ausdruck:

Die Lösungsmenge dieses Gleichungssystems lautet

Jeder Vektor aus dieser Menge ist ein Eigenvektor der Matrix  zum Eigenwert
zum Eigenwert  . Da der Eigenwert
. Da der Eigenwert  eine einfache Nullstelle des charakteristischen Polynoms
eine einfache Nullstelle des charakteristischen Polynoms  ist, ist seine algebraische Vielfachheit gleich 1. Ebenso ist seine geometrische Vielfachheit gleich 1, da sein Eigenraum eindimensional ist. Analog kann man für die anderen beiden Eigenwerte die Eigenvektoren bestimmen. Zum Eigenwert
ist, ist seine algebraische Vielfachheit gleich 1. Ebenso ist seine geometrische Vielfachheit gleich 1, da sein Eigenraum eindimensional ist. Analog kann man für die anderen beiden Eigenwerte die Eigenvektoren bestimmen. Zum Eigenwert  sind die Eigenvektoren aus der Menge
sind die Eigenvektoren aus der Menge
 .
.
Für  ist jeder Vektor der Menge
ist jeder Vektor der Menge

ein Eigenvektor.
