Video

Quiz

Hier geht's zum Video „Kreuzprodukt / Vektorprodukt“

Hier geht's zum Video „Skalarprodukt“

Spatprodukt

Wichtige Inhalte in diesem Video

Spatprodukt einfach erklärt

Spatprodukt Beispiel

Spatprodukt Determinante

In diesem Artikel erklären wir dir, was das Spatprodukt ist und wie du es berechnest. Du möchtest das Thema in kürzester Zeit verstehen? Dann schau dir unser Video dazu an.

Inhaltsübersicht

Spatprodukt einfach erklärt

im Videozur Stelle im Video springen

Mit dem Spatprodukt kannst du das Volumen berechnen, das von drei Vektoren eingespannt wird. Den Körper, den die drei Vektoren einspannen, nennt man Spat.

Spatprodukt

Das Spatprodukt der drei Vektoren $\vec{a}=\left(\begin{array}{c} a_1 \\ a_2\\ a_3 \end{array}\right)$ , $\vec{b}=\left(\begin{array}{c} b_1 \\ b_2\\ b_3 \end{array}\right)$ und $\vec{c}= \left(\begin{array}{c} c_1 \\ c_2\\ c_3 \end{array}\right)$ berechnest du mit

$(\vec{a} \times \vec{b}) \cdot \vec{c}$ oder mit
der Determinante $\begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix}$ .

Beispiel: Betrachte die Vektoren $\vec{a} = \left(\begin{array}{c} -4 \\ 3 \\ -2 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} 1 \\ -6 \\ 1 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} -1 \\ 0 \\ 2 \end{array}\right)$ , dann erhältst du

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \left( \left(\begin{array}{c} -4 \\ 3 \\ -2 \end{array}\right) \times \left(\begin{array}{c} 1 \\ -6 \\ 1 \end{array}\right) \right) \cdot \left(\begin{array}{c} -1 \\ 0 \\ 2 \end{array}\right) = 51$

oder $\begin{vmatrix} -4 & 1 & -1 \\ 3 & -6 & 0 \\ -2 & 1 & 2 \end{vmatrix}=51$ .

Spat, Spatprodukt, Volumen eines Spats, Spatprodukt berechnen, Spatprodukt bestimmen — Der Spat dreier Vektoren

Hinweis: Mit dem Skalarprodukt kannst du die Fläche berechnen, die von zwei Vektoren eingespannt wird.

Spatprodukt berechnen

Das Spatprodukt von drei Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ berechnest du mit der Formel $(\vec{a} \times \vec{b}) \cdot \vec{c}$ .

Dabei bezeichnest du mit 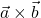$\vec{a} \times \vec{b}$ das Kreuzprodukt der beiden Vektoren und das Malzeichen stellt das Skalarprodukt zweier Vektoren dar.

Spatprodukt Beispiel

im Videozur Stelle im Video springen

Betrachte zum Beispiel die Vektoren $\vec{a} = \left(\begin{array}{c} 4 \\ -6 \\ -5 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} -1 \\ 0 \\ 2 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} 5 \\ 5 \\ 0 \end{array}\right)$ . Zuerst benötigst du das Kreuzprodukt der beiden Vektoren $\vec{a}$ und $\vec{b}$

$\vec{a} \times \vec{b} = \left(\begin{array}{c} 4 \\ -6 \\ -5 \end{array}\right) \times \left(\begin{array}{c} -1 \\ 0 \\ 2 \end{array}\right) = \left(\begin{array}{c} -12 + 0 \\ 5 - 8 \\ 0 - 6 \end{array}\right) = \left(\begin{array}{c} -12 \\ -3 \\ -6 \end{array}\right).$

Danach berechnest du dann das Skalarprodukt von diesem Vektor mit dem Vektor $\vec{c}$

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \left(\begin{array}{c} -12 \\ -3 \\ -6 \end{array}\right) \cdot \left(\begin{array}{c} 5 \\ 5 \\ 0 \end{array}\right) = -12 \cdot 5 - 3 \cdot 5 - 6 \cdot 0 = -75.$

Der Betrag des Spatprodukts |-75|=75 ist dann das Volumen des Spats.

Was ist ein Spat in Mathe?

Ein Spat ist ein geometrischer Körper , der sechs Parallelogramme als Seitenflächen hat. Diese Parallelogramme sind deckungsgleich (paarweise kongruent). An sich ist ein Spat also nichts anderes als ein Quader, der statt Rechtecken Parallelogramme als Seitenflächen besitzt. Der Spat wird auch Parallelepiped genannt.

Spatprodukt Determinante

im Videozur Stelle im Video springen

Um das Spatprodukt dreier Vektoren $\vec{a} = \left(\begin{array}{c} a_1 \\ a_2\\ a_3 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} c_1 \\ c_2 \\ c_3 \end{array}\right)$ zu berechnen, kannst du auch die Determinante einer 3×3 Matrix verwenden. Dabei schreibst du die Vektoren einfach in eine Matrix und berechnest dann die Determinante

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix}.$

Beispiel

Für die Vektoren $\vec{a} = \left(\begin{array}{c} 1 \\ -3 \\ -6 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} 6 \\ 5 \\ 2 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} 1 \\ -6 \\ -4 \end{array}\right)$ lässt sich das Spatprodukt dadurch berechnen, in dem du die einzelnen Vektoren in eine Matrix schreibst und dann die Determinante berechnest

$\begin{vmatrix} 1 & 6 & 1 \\ -3 & 5 & -6 \\ -6 & 2 & -4 \end{vmatrix} = -1 \cdot 5 \cdot 4 + 6 \cdot 6 \cdot 6 - 1 \cdot 3 \cdot 2 + 6 \cdot 5 \cdot 1+ 2 \cdot 6 \cdot 1 - 4 \cdot 3 \cdot 6 = 160.$

Wir haben dabei die Regel von Sarrus verwendet.

Weitere Themen der Vektorrechnung

Neben dem Spatprodukt gibt es noch weitere Themen, die sich mit Vektoren beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:

Spatprodukt Aufgaben

Im folgenden Abschnitt geben wir dir zwei Aufgaben mit Lösungen, um das Berechnen des Spatprodukts zu üben.

Aufgabe 1: Spatprodukt berechnen

Berechne das Spatprodukt der drei Vektoren $\vec{a} = \left(\begin{array}{c} -2 \\ 1 \\ 4 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} 3 \\ -1 \\ 0 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} -3 \\ 4 \\ 2 \end{array}\right)$ .

Lösung Aufgabe 1

Berechne zuerst das Kreuzprodukt der beiden Vektoren $\vec{a}$ und $\vec{b}$

$\vec{a} \times \vec{b} = \left(\begin{array}{c} 0+4 \\ 12+0 \\ 2-3 \end{array}\right)=\left(\begin{array}{c} 4 \\ 12 \\ -1 \end{array}\right).$

Setzt du das in die Formel des Spatprodukts ein, dann erhältst du

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \left(\begin{array}{c} 4 \\ 12 \\ -1 \end{array}\right) \cdot \left(\begin{array}{c} -3 \\ 4 \\ 2 \end{array}\right) = - 4 \cdot 3 + 12 \cdot 4 - 1 \cdot 2 = 34.$

Aufgabe 2: Spatprodukt Volumen

Berechne das Volumen V_S des Spats, das durch die drei Vektoren $\vec{a} = \left(\begin{array}{c} 3 \\ -4 \\ -3 \end{array}\right)$ , $\vec{b} = \left(\begin{array}{c} -2 \\ 4 \\ -1 \end{array}\right)$ und $\vec{c} = \left(\begin{array}{c} 4 \\ -2 \\ -3 \end{array}\right)$ aufgespannt wird.

Lösung Aufgabe 2

Das Volumen des Spats berechnest du mit der Formel $|(\vec{a} \times \vec{b}) \cdot \vec{c}|$ , wofür du also das Spatprodukt der drei Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ benötigst. Das heißt, du berechnest zuerst das Kreuzprodukt von $\vec{a}$ und $\vec{b}$

$\vec{a} \times \vec{b} = \left(\begin{array}{c} 4 + 12 \\ 6 + 3 \\ 12 - 8 \end{array}\right) = \left(\begin{array}{c} 16 \\ 9 \\ 4 \end{array}\right).$

Für das Spatprodukt bekommst du damit

$(\vec{a} \times \vec{b}) \cdot \vec{c} = \left(\begin{array}{c} 16 \\ 9 \\ 4 \end{array}\right) \cdot \left(\begin{array}{c} 4 \\ -2 \\ -3 \end{array}\right) = 16 \cdot 4 - 9 \cdot 2 - 4 \cdot 3 = 34$ .

Um das Volumen des Spats zu bestimmen, musst du noch den Betrag des Spatpodukts berechnen

V_S = |34| = 34 .

Der Spat hat also ein Volumen von 34.

zur Videoseite: Spatprodukt

Beliebte Inhalte aus dem Bereich Lineare Algebra

Vektor Multiplikation

Kreuzprodukt / Vektorprodukt

Flächeninhalt Dreieck Vektoren

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .