Orthogonale Projektion
In diesem Artikel zeigen wir dir, was eine orthogonale Projektion ist und welche Rolle das Skalarprodukt dabei spielt.
Wenn du die orthogonale Projektion in unter 5 Minuten verstehen willst, dann schau dir gerne unser Theorievideo dazu an.
Schau dir gerne auch noch unsere Videos zu einer Übungsaufgabe und einer beispielhaften Klausuraufgabe an, um die orthogonale Projektion sofort praktisch zu üben.
Inhaltsübersicht
Orthogonale Projektion einfach erklärt
In der Geometrie wird ein Punkt auf eine Gerade oder eine Ebene senkrecht projiziert, während in der linearen Algebra das Konzept auf höherdimensionale Vektorräume verallgemeinert wird.
Orthogonale Projektion Skalarprodukt
Das Skalarprodukt behandelt die Multiplikation zweier Vektoren und lässt sich am Beispiel der Vektoren  und
und  formulieren:
formulieren:

Bei einer Multiplikation von Vektoren spielt auch der Winkel, der durch die beiden Vektoren aufgespannt wird, eine Rolle. Ein Sonderfall existiert, falls dieser Winkel 90° beträgt. Hier wird der Kosinus null und damit auch das komplette Produkt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Orthogonale Projektion von Vektoren
Bei dieser Projektion wird ein Vektor senkrecht auf einen anderen Vektor projiziert. Das dient in diesem Artikel als Basisfall, auf dem später aufgebaut werden soll. Folgende Grafik verdeutlicht den Zusammenhang:
Herleitung Vektorprojektion
Es lassen sich zwei Gleichungen herleiten. Sie dienen allgemein in jeder senkrechten Projektion als Grundlage. Die erste beinhaltet den Zusammenhang, dass das projizierte Objekt ein Bestandteil von dem zugrunde gelegten Objekt ist. In dem Fall muss  ein Teil von
ein Teil von  sein und sich somit durch einen Faktor und dem Vektor
sein und sich somit durch einen Faktor und dem Vektor  selbst ausdrücken lassen. Die zweite beschreibt die Orthogonalität der beiden Vektoren
selbst ausdrücken lassen. Die zweite beschreibt die Orthogonalität der beiden Vektoren  und
und  , welcher das Lot auf
, welcher das Lot auf  darstellt. Dies kann mithilfe des Skalarproduktes festgestellt werden.
darstellt. Dies kann mithilfe des Skalarproduktes festgestellt werden.
So ergeben sich die zwei Zusammenhänge:
Erste Gleichung: 
Zweite Gleichung: 
Es befinden sich aktuell drei unbekannte Variablen in den Gleichungen, weshalb eine ausgetauscht werden muss. Nur so kann eine eindeutige Lösung berechnet werden.  darf in der zweiten Gleichung wie folgt ersetzt werden:
darf in der zweiten Gleichung wie folgt ersetzt werden:

Daraufhin wird die erste Gleichung in die zweite eingesetzt:

Nach dem Auflösen erhält man den Skalierungsfaktor x als:

Mit der Hilfe der ersten Gleichung kann jetzt der zusammengesetzte Vektor  berechnet werden.
berechnet werden.

Orthogonale Projektion berechnen
Die so hergeleiteten Formeln werden auf folgendes Beispiel angewandt. Dafür werden die zwei Vektoren  und
und  gebildet. Nun soll
gebildet. Nun soll  auf
auf  senkrecht projiziert werden. Der projizierte Vektor
senkrecht projiziert werden. Der projizierte Vektor  ergibt sich mit der aus den zwei Gleichungen hergeleiteten Formel:
ergibt sich mit der aus den zwei Gleichungen hergeleiteten Formel:

Die einzelnen Teile des Bruches lassen sich wie folgt berechnen:


Im nächsten Schritt entsteht so:
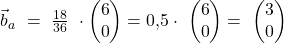
Damit ist der senkrecht projizierte Vektor  und hat einen Skalierungsfaktor von 0,5 gegnüber
und hat einen Skalierungsfaktor von 0,5 gegnüber  .
.
Orthogonalprojektion auf eine Gerade
Eine Projektion eines Punktes auf eine Gerade lässt sich grafisch wie folgt darstellen.
Die Linie von Punkt P nach Punkt P‘ wird Lot und P‘ wird Lotfußpunkt genannt. Hinzu kommt der Richtungsvektor 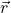 der Geraden g und der Aufpunkt
der Geraden g und der Aufpunkt  . Die Herleitung der Berechnungen ist der vorherigen Herleitung für die orthogonale Projektion von Vektoren sehr ähnlich, denn die Punkte können auch als Ortsvektoren angesehen werden. Diese Notation muss jetzt in die zwei Gleichungen übertragen werden. Der Punkt P‘ ist dabei ein Teil von der Geraden g und das Lot von P nach P‘ muss senkrecht auf g stehen. So ergeben sich die Koordinaten des Punktes P‘, der durch die orthogonale Projektion entstanden ist, als:
. Die Herleitung der Berechnungen ist der vorherigen Herleitung für die orthogonale Projektion von Vektoren sehr ähnlich, denn die Punkte können auch als Ortsvektoren angesehen werden. Diese Notation muss jetzt in die zwei Gleichungen übertragen werden. Der Punkt P‘ ist dabei ein Teil von der Geraden g und das Lot von P nach P‘ muss senkrecht auf g stehen. So ergeben sich die Koordinaten des Punktes P‘, der durch die orthogonale Projektion entstanden ist, als:

In dieser Formel werden die Punkte P‘, P und r0 als Ortsvektoren aufgefasst und deshalb in der Notation der Vektoren geschrieben.
Orthogonalität auf eine Ebene
Ebenfalls kann ein Punkt auf eine Ebene im dreidimensionalem Raum senkrecht abgebildet werden. Dies sieht dann wie folgt aus:
Auch hier lassen sich die zwei Gleichungen anwenden und dienen als Ausgangspunkt für die Herleitung der allgemeinen Formel. Der projizierte Punkt  muss Teil der Ebene E sein und das Lot von x auf die Ebene muss senkrecht auf der Fläche stehen. Hier ist dann die Ebene in der Parameterform gegeben:
muss Teil der Ebene E sein und das Lot von x auf die Ebene muss senkrecht auf der Fläche stehen. Hier ist dann die Ebene in der Parameterform gegeben:

Die reellen Parameter sind y und z und die Vektoren  und
und  sind die Spannvektoren der Ebene, welche nicht kollinear sind. Kollinear bezeichnet parallele oder anti-parallele Vektoren. Falls die Spannvektoren der Ebene nicht orthogonal
zueinander sind, muss ein Vektor gefunden werden, der diese Eigenschaft erfüllt. Dies ist der Vektor
sind die Spannvektoren der Ebene, welche nicht kollinear sind. Kollinear bezeichnet parallele oder anti-parallele Vektoren. Falls die Spannvektoren der Ebene nicht orthogonal
zueinander sind, muss ein Vektor gefunden werden, der diese Eigenschaft erfüllt. Dies ist der Vektor  . Er ist orthogonal zu
. Er ist orthogonal zu  und wird wie folgt aus
und wird wie folgt aus  berechnet:
berechnet:

Die Formel für die Berechnung der Koordinaten des senkrecht abgebildeten Punktes ist:

Dabei folgt die Herleitung dieser Berechnung für die Koordinaten des orthogonal projizierten Punktes derselben Logik, wie bei unserem Basisfall.
Alternativ zu diesem Vorgehen kann die Orthogonalprojektion auch durch den Schnittpunkt der Lotgeraden mit der Ebene berechnet werden. Aus einem Vektorprodukt der Spannvektoren  und
und  entsteht der Normalenvektor
entsteht der Normalenvektor  der Ebene E. Die Berechnung erfolgt dann nach folgender Formel:
der Ebene E. Die Berechnung erfolgt dann nach folgender Formel:
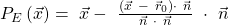
Orthogonale Projektion lineare Algebra
Die Orthogonalprojektion von Vektoren wird in der linearen Algebra in sogenannten Vektorräumen verallgemeinernd behandelt. Ein Vektorraum ist eine nicht leere Menge, deren Elemente bestimmte Eigenschaften aufweisen. Ein Beispiel wäre das Vorhandensein eines Nullvektors oder das Funktionieren des Distributivgesetzes. Beispielsweise ist der Raum  ein Vektorraum. Des Weiteren gibt es Untervektorräume. Dieser ist definiert als ein Vektorraum innerhalb eines größeren Vektorraums.
ein Vektorraum. Des Weiteren gibt es Untervektorräume. Dieser ist definiert als ein Vektorraum innerhalb eines größeren Vektorraums.
Für die orthogonale Projektion in solchen Räumen gilt wieder der Zusammenhang, dass zwei Vektoren  und
und  in einem Vektorraum orthogonal sind, wenn ihr Skalarprodukt
in einem Vektorraum orthogonal sind, wenn ihr Skalarprodukt  ,
, miteinander gleich null ist.
miteinander gleich null ist.
Will man einen Vektor aus dem Vektorraum V in einen Untervektorraum U projizieren, lassen sich dieselben zwei Gleichungen wie im Basisfall als allgemeiner Startpunkt formulieren. Wenn die Vektoren 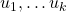 eine Orthogonalbasis eines Untervektorraums U mit der Dimension k darstellen, dann hat jeder Vektor u, der Element von U ist, eine eindeutige Darstellung als Linearkombination
eine Orthogonalbasis eines Untervektorraums U mit der Dimension k darstellen, dann hat jeder Vektor u, der Element von U ist, eine eindeutige Darstellung als Linearkombination  dieser Basisvektoren. Somit muss sich also auch die Orthogonalprojektion
dieser Basisvektoren. Somit muss sich also auch die Orthogonalprojektion  des Vektors v auf den Untervektorraum U als eine solche Linearkombination darstellen lassen.
des Vektors v auf den Untervektorraum U als eine solche Linearkombination darstellen lassen.

Weiterhin muss der Differenzvektor  orthogonal zu sämtlichen Vektoren aus U stehen. Dies gilt bereits, wenn er zu den Basisvektoren
orthogonal zu sämtlichen Vektoren aus U stehen. Dies gilt bereits, wenn er zu den Basisvektoren 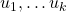 von U orthogonal ist. Die gerade formulierte Bedingung lautet nach der Definition der Orthogonalität wie folgt:
von U orthogonal ist. Die gerade formulierte Bedingung lautet nach der Definition der Orthogonalität wie folgt:
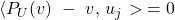 und
und 
Die zwei Gleichungen dienen als Startpunkt für die Herleitung der Koordinaten des projizierten Vektors. Durch Einsetzen und Umformen ergeben sich die Koordinaten folgendermaßen:

Der Laufindex i spiegelt die Dimensionen wider. Dabei ist zu beachten, dass die Vektoren 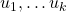 eine Orthogonalbasis des Untervektorraums U darstellen.
eine Orthogonalbasis des Untervektorraums U darstellen.
Orthogonale Projektion Übungsaufgabe
Nun betrachten wir eine Übungsaufgabe für die orthogonale Projektion eines Vektors.
Gegeben sei im dreidimensionalen euklidischen Raum die folgende Ebene

Berechne die orthogonale Projektion des Vektors  auf die Ebene
auf die Ebene  .
.
Bevor du aber losrechnest noch ein kleiner Tipp: um das Vorgehen aus unserem Video anwenden zu können, musst du zuerst die Darstellung der Ebene E in die richtige Form bringen.
Die Lösung und die Erklärung dieser Aufgabe findest du in unseren jeweiligen Übungsvideo .
Orthogonale Projektion Klausuraufgabe
Nachfolgend findest du eine Aufgabe, mit der du dich auf deine Klausur vorbereiten kannst.
In der Aufgabenstellung ist die Matrix A

und die Definition des Skalarprodukts  gegeben:
gegeben:

für alle 
Außerdem seien die Vektoren  ,
, 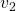 und
und  folgendermaßen angeben:
folgendermaßen angeben:
 ,
,  und
und 
Bestimme nun bezüglich des gegebenen Skalarprodukts  die orthogonale Projektion von
die orthogonale Projektion von  auf den von
auf den von  und
und 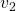 aufgespannten Untervektorraum
aufgespannten Untervektorraum  .
.
Du musst bei dieser Aufgabe vor allem darauf achten nicht das Standardskalarprodukt zu wählen, sondern mit dem hier vorgegebenen Skalarprodukt zu arbeiten.
Die Lösung zu dieser Aufgabe mit einem verständlichen Rechenweg findest du in unserem Klausurvideo .




