Vektor Multiplikation
Wie funktioniert die Vektor Multiplikation? Wir zeigen dir die verschiedenen Arten, wie du Vektoren multiplizieren kannst und erklären dir, wofür du sie brauchst!
Inhaltsübersicht
Vektor Multiplikation — Skalarprodukt und Kreuzprodukt
Die Vektor Multiplikation ist ein wichtiges Hilfsmittel in der Geometrie. Du brauchst sie zum Beispiel, um den Winkel zwischen zwei Vektoren zu bestimmen. Auch wenn du den Normalenvektor einer Ebene berechnen willst, kommt dabei das Multiplizieren von Vektoren zum Einsatz.
Aber Achtung! Es gibt nicht nur eine einzige Vektor Multiplikation! Konkret unterscheidest du zwei Arten, Vektoren zu multiplizieren:
- Das Skalarprodukt
 ,
, 
- das Kreuzprodukt
(auch: Vektorprodukt)
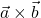
Ihr wichtigster Unterschied ist das Ergebnis. Multiplizierst du zwei Vektoren im Skalarprodukt, kommt eine Zahl (ein „Skalar“) heraus. Das Kreuzprodukt zweier Vektoren ergibt dagegen wieder einen Vektor.
In jedem Fall müssen beide Vektoren aus gleich vielen Zahlen (Einträgen) bestehen, damit du sie multiplizieren kannst.
Schau dir gleich mal an, wie das mit dem Skalarprodukt und dem Kreuzprodukt genau funktioniert und wann du welche Art von Vektor Multiplikation brauchst! Eine anschauliche Erklärung dazu findest du auch in unserem Video !
Vektor Multiplikation — Skalarprodukt
Das Skalarprodukt verwendest du, um zwei Vektoren mit derselben Anzahl an Einträgen zu multiplizieren. Als Ergebnis bekommst du eine einzelne Zahl. Zur Berechnung des Skalarprodukts von zwei Vektoren  und
und  gehören zwei Schritte:
gehören zwei Schritte:
- Zuerst multiplizierst du die Einträge der Vektoren komponentenweise: Das heißt, du rechnest die oberste Zahl des einen Vektors mal die oberste Zahl des anderen Vektors (a1 · b1). Genauso multiplizierst du auch die mittleren (a2 · b2) und unteren (a3 · b3) Einträge der beiden Vektoren.
- Anschließend rechnest du die Ergebnisse dann zusammen: (a1 · b1) + (a2 · b2) + (a3 · b3)
Insgesamt kannst du dir für die Multiplikation von Vektoren mit dem Skalarprodukt die folgende Formel merken:

Mit konkreten Zahlen sieht das dann zum Beispiel so aus:

Aber wozu ist das Skalarprodukt gut? Du brauchst es beispielsweise um…
- … den Betrag eines Vektors zu berechnen
- … zu prüfen, ob zwei Vektoren senkrecht aufeinander stehen
- … den Winkel zwischen zwei Vektoren zu bestimmen
Wie genau die Multiplikation von Vektoren dort zum Einsatz kommt, erfährst du in den nächsten Abschnitten!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Skalarprodukt — Vektoren auf Orthogonalität prüfen
Am Skalarprodukt kannst du ablesen, ob zwei Vektoren  und
und  senkrecht (orthogonal)
zueinander stehen. Ergeben die beiden Vektoren multipliziert im Skalarprodukt 0, sind sie orthogonal zueinander (
senkrecht (orthogonal)
zueinander stehen. Ergeben die beiden Vektoren multipliziert im Skalarprodukt 0, sind sie orthogonal zueinander ( ) — wie in diesem Beispiel:
) — wie in diesem Beispiel:
Das Skalarprodukt der Vektoren  und
und  ergibt 0:
ergibt 0: 
 und
und  stehen also senkrecht zueinander.
stehen also senkrecht zueinander.
Skalarprodukt — Winkel zwischen zwei Vektoren
Auch wenn das Skalarprodukt von zwei Vektoren nicht 0 ergibt, kannst du diese Art der Vektor Multiplikation nutzen, um etwas über die Lage der Vektoren zueinander herauszufinden. Du brauchst das Skalarprodukt nämlich in der Formel für den Winkel φ zwischen zwei Vektoren  und
und  :
:
![Rendered by QuickLaTeX.com \[\textcolor{red}{\varphi} = \textrm{cos}^{-1}(\frac{\textcolor{orange}{\vec{a}} \circ \textcolor{orange}{\vec{b}}}{\vert \textcolor{orange}{\vec{a}} \vert \cdot \vert \textcolor{orange}{\vec{b}} \vert})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-04b2a357918c85b1537f73c3addf93bf_l3.png)
Den Winkel φ zwischen den Vektoren  und
und  berechnest du also insgesamt in 4 Schritten:
berechnest du also insgesamt in 4 Schritten:
- Berechne das Skalarprodukt aus den beiden Vektoren:

- Bestimme den Betrag des ersten Vektors. Dazu brauchst du auch wieder das Skalarprodukt:

- Bestimme nun den Betrag des zweiten Vektors:

-
Setze die drei Werte dann in die Formel zur Berechnung des Winkels φ ein:
![Rendered by QuickLaTeX.com \[\textcolor{red}{\varphi} = \textrm{cos}^{-1}(\frac{\textcolor{orange}{\vec{a}} \circ \textcolor{orange}{\vec{b}}}{\vert \textcolor{orange}{\vec{a}} \vert \cdot \vert \textcolor{orange}{\vec{b}} \vert})\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-04b2a357918c85b1537f73c3addf93bf_l3.png)
Du bekommst dann das Ergebnis:
![Rendered by QuickLaTeX.com \[\textcolor{red}{\varphi} = \textrm{cos}^{-1}(\frac{2}{1 \cdot \sqrt{8}}) = \textcolor{red}{45^{\circ}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d952c6aa6b4065993609ecfe2cdfcd83_l3.png)
Klasse! Schau dir als nächstes an, wie die Multiplikation von Vektoren mit dem Kreuzprodukt funktioniert und wann du zwei Vektoren auf diese Art multiplizierst!
Vektor Multiplikation — Kreuzprodukt
Das Kreuzprodukt (auch: Vektorprodukt) wendest du meistens bei Vektoren mit drei Einträgen an. Hier ist die Vektor Multiplikation etwas komplizierter als beim Skalarprodukt. Für zwei Vektoren
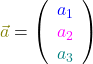 und
und 
berechnest du das Kreuzprodukt mit der folgenden Formel:

Als Ergebnis von Vektor mal Vektor kommt hier also wieder ein Vektor mit derselben Anzahl an Einträgen heraus.
Wende das Kreuzprodukt direkt mal auf die Vektoren  und
und  an:
an:

Aber was für eine Bedeutung hat der Vektor, den du als Ergebnis der Vektor Multiplikation mit dem Kreuzprodukt bekommst?
Kreuzprodukt — Anwendung: Normalenvektor
Tatsächlich hat der Ergebnis-Vektor  eine ganz besondere Eigenschaft: Er steht nämlich senkrecht zu
eine ganz besondere Eigenschaft: Er steht nämlich senkrecht zu  und
und  .
.
Sind  und
und  die Richtungsvektoren einer Ebene E, so nennst du
die Richtungsvektoren einer Ebene E, so nennst du  den Normalenvektor
von E.
den Normalenvektor
von E.
So ist beispielsweise  der Normalenvektor zu der Ebene, die von
der Normalenvektor zu der Ebene, die von  und
und  aufgespannt wird.
aufgespannt wird.
Kreuzprodukt — Anwendung: Flächeninhalt Parallelogramm
Außerdem kannst du mit dem Kreuzprodukt den Flächeninhalt des Parallelogramms berechnen, das von zwei Vektoren aufgespannt wird.
Der Flächeninhalt dieses Parallelogramms entspricht nämlich dem Betrag des Vektors, den du als Ergebnis des Kreuzproduktes von  und
und  erhältst:
erhältst:

Dieses Parallelogramm aus  und
und  hat demnach den Flächeninhalt
hat demnach den Flächeninhalt 
Übrigens: Im Gegensatz zum Skalarprodukt ist es beim Kreuzprodukt nicht egal, in welcher Reihenfolge du die Vektoren multiplizierst! Drehst du die Vektoren um, ändert sich das Vorzeichen:

Skalarprodukt vs. Vektorprodukt — Unterschiede im Überblick
Schau dir die Unterschiede zwischen dem Skalarprodukt und dem Kreuzprodukt gleich nochmal im Überblick an:
| Skalarprodukt | Kreuzprodukt/Vektorprodukt | |
| Schreibweisen |  |
 |
| Ergebnis | Zahl | Vektor |
| Anwendung |
|
|
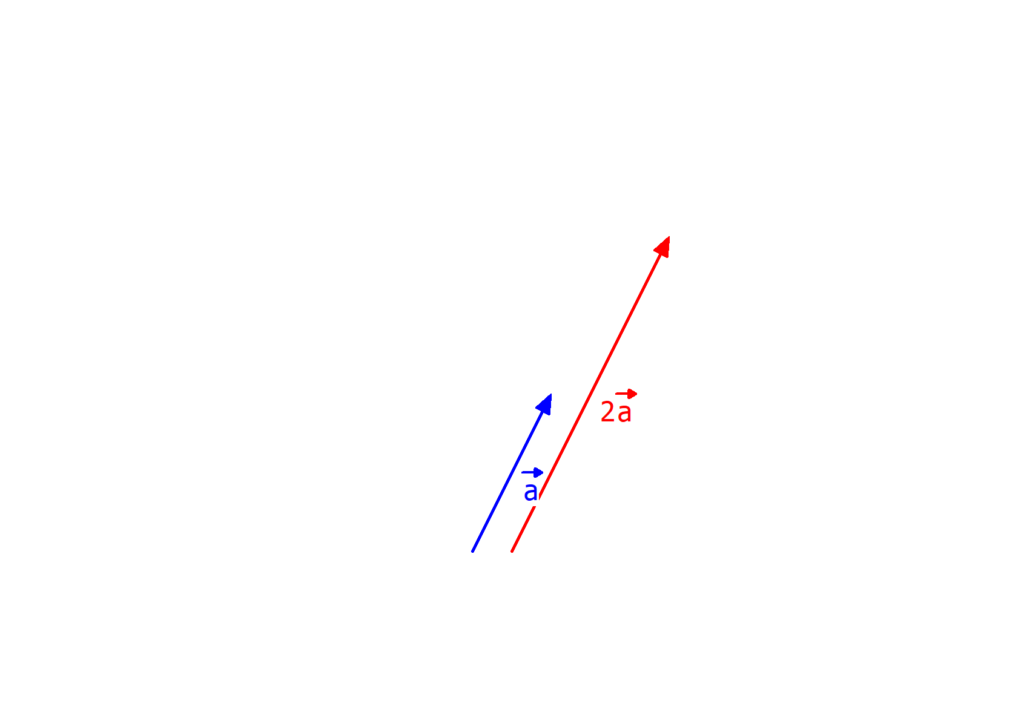
Vektor mit Zahl multiplizieren
Statt Vektor mal Vektor zu rechnen, kannst du einen Vektor  auch mit einer Zahl c multiplizieren. Das Ergebnis ist wieder ein Vektor. Wie der aussieht, hängt von der Zahl ab, mit der du den Vektor mal nimmst:
auch mit einer Zahl c multiplizieren. Das Ergebnis ist wieder ein Vektor. Wie der aussieht, hängt von der Zahl ab, mit der du den Vektor mal nimmst:
- So erhältst du zum Beispiel den Gegenvektor von
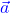 , wenn du mit c = -1 multiplizierst.
, wenn du mit c = -1 multiplizierst.
-
|c| > 1: Vektor
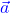 wird länger („gestreckt“)
wird länger („gestreckt“)
-
|c| < 1: Vektor
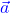 wird kürzer („gestaucht“)
wird kürzer („gestaucht“)
Vektor Multiplikation — die wichtigsten Fragen
-
Was versteht man unter Vektor Multiplikation?
Bei der Vektor Multiplikation unterscheidest du zwei Arten: das Skalarprodukt , bei dem als Ergebnis eine Zahl herauskommt, und das Kreuzprodukt (Vektorprodukt). Dort ist das Ergebnis wieder ein Vektor.
-
Wie multipliziert man Vektoren?
Bei der Multiplikation von Vektoren im Skalarprodukt multiplizierst du ihre Einträge komponentenweise und addierst anschließend die Produkte. Das Kreuzprodukt hat eine eigene Formel, die du dir merken solltest.
-
Wozu braucht man die Vektor Multiplikation?
Die Vektor Multiplikation in Form des Skalarprodukts brauchst du zum Beispiel, um Orthogonalität zu überprüfen, den Betrag eines Vektors oder den Winkel zwischen zwei Vektoren zu berechnen. Mit dem Kreuzprodukt bestimmst du den Normalenvektor und kannst den Flächeninhalt eines Parallelogramms ausrechnen.
Vektorrechnung
Egal ob Skalarprodukt oder Kreuzprodukt — die Multiplikation von Vektoren ist für dich nun kein Problem mehr! Aber wie war das nochmal mit den anderen Grundrechenarten bei Vektoren? In unserem Video bekommst du nochmal einen Überblick zum Thema Vektorrechnung. Schau es dir direkt mal an!
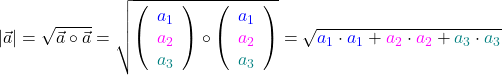
 wäre also:
wäre also: