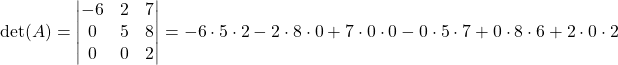Determinante 3×3
In diesem Artikel zeigen wir dir, wie du die 3×3 Determinante einer Matrix berechnest. Du möchtest die 3×3 Determinante in nur kurzer Zeit bestimmen können? Dann schau dir unser Video dazu an.
Inhaltsübersicht
Determinante 3×3 einfach erklärt
Die 3×3 Determinante einer Matrix  , berechnest du mit der Regel von Sarrus.
, berechnest du mit der Regel von Sarrus.
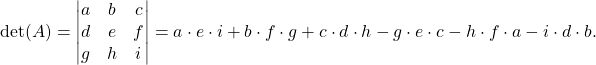
Dabei addierst du die Produkte der Elemente der Diagonalen von links oben nach rechts unten (blau) und ziehst davon die Produkte der Diagonalen von links unten nach rechts oben (rot) ab.
Beispiel: Für die 3×3 Determinante der Matrix  ergibt sich damit
ergibt sich damit

 .
.
Hinweis: Für die Notation der Determinante findest du die Schreibweisen  oder
oder  .
.
Determinante 3×3 berechnen
Um nicht die obige Formel auswendig lernen zu müssen, gibt es eine einfache Methode, wie du dir die Berechnung der Determinante einer 3×3 Matrix leicht merken kannst. Gehe dabei wie folgt vor:
Schreibe zuerst die Matrix A auf und notiere die ersten zwei Spalten der Matrix dahinter.

Als nächstes betrachtest du die Einträge in der Hauptdiagonale
und danach bildest du das Produkt  . Somit erhältst du den ersten Summanden der Determinante
. Somit erhältst du den ersten Summanden der Determinante
 .
.
Um die nächsten zwei Summanden der 3×3 Determinante zu bestimmen, betrachtest du die Diagonalen weiter rechts.
Das heißt, du addierst zuerst das Produkt 
und anschließend das Produkt 
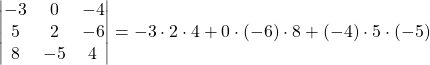 .
.
Als nächstes betrachtest du die Nebendiagonale
und ziehst das Produkt  ab
ab
 .
.
Das Gleiche machst du mit den Diagonalen neben der Nebendiagonale. Du ziehst zuerst  ab
ab
und subtrahierst danach  .
.


Insgesamt ist dann die 3×3 Determinante von A gegeben durch
 .
.
Merke: Diese Vorgehensweise wird Regel von Sarrus genannt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 1
Schauen wir uns dazu ein Beispiel an. Gehen wir davon aus, du sollst die 3×3 Determinante der Matrix  mit der Regel von Sarrus berechnen, dann erhältst du
mit der Regel von Sarrus berechnen, dann erhältst du
 .
.
 .
.
Weitere Themen zur Determinante
Neben der Determinante einer 3×3 Matrix haben wir noch weitere Themen für dich vorbereitet, die sich mit der Determinante beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:
Determinante 3×3 Aufgaben
In diesem Abschnitt kannst du die Berechnung einer 3×3 Determinante üben, indem du die folgenden Aufgaben löst.
Aufgabe 1: Determinante einer 3×3 Matrix
Berechne die 3×3 Determinante der Matrix  mit der Regel von Sarrus.
mit der Regel von Sarrus.
Lösung Aufgabe 1
Um die 3×3 Determinante der Matrix A zu berechnen, verwendest du die Regel von Sarrus.



Aufgabe 2: 3×3 Determinante
Bestimme die Determinante der 3×3 Matrix  .
.
Lösung Aufgabe 2
Die Lösung der 3×3 Determinante ergibt sich mit der Regel von Sarrus durch

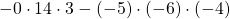
 .
.








 . Dabei gehst du genauso vor, wie im vorherigen Beispiel.
. Dabei gehst du genauso vor, wie im vorherigen Beispiel.