Inverse Matrix
Du willst wissen, was eine inverse Matrix ist? Dann bist du hier genau richtig! Alles Wichtige erfährst du in kürzester Zeit, wenn du unser Video anschaust!
Inhaltsübersicht
Inverse Matrix einfach erklärt
Erinnere dich kurz an die Potenzgesetze. Da gab es die Zahl hoch minus 1, das steht für den Kehrwert einer Zahl.

So eine ähnliche Regel gibt es auch für Matrizen. Eine Matrix hoch minus 1 steht dabei für die inverse Matrix. Multiplizierst du eine Matrix  mit ihrer inversen Matrix
mit ihrer inversen Matrix  , dann erhältst du die Einheitsmatrix
, dann erhältst du die Einheitsmatrix
 . Das ist die Matrix, bei der alle Einträge auf der Hauptdiagonalen 1 sind.
. Das ist die Matrix, bei der alle Einträge auf der Hauptdiagonalen 1 sind.
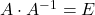

Die inverse Matrix  ist die Matrix, die multipliziert mit der ursprünglichen Matrix
ist die Matrix, die multipliziert mit der ursprünglichen Matrix  die Einheitsmatrix
die Einheitsmatrix  ergibt.
ergibt.
Zum Berechnen der Inversen bietet sich der Gauß-Algorithmus , die Adjunkte oder die Cramersche Regel an. Mehr dazu findest du im Video zum Thema Inverse Matrix berechnen .
Invertierbare Matrix
Leider ist nicht jede beliebige Matrix invertierbar, sondern nur solche Matrizen, die bestimmte Voraussetzungen erfüllen. Es stellt sich also die Frage, wann ist eine Matrix invertierbar? Dazu musst du prüfen, ob du eine quadratische Matrix vorliegen hast und ob die Determinante der Matrix ungleich Null ist.

Die Beispielmatrix  hat drei Zeilen und drei Spalten, sie ist also eine quadratische Matrix. Außerdem gilt
hat drei Zeilen und drei Spalten, sie ist also eine quadratische Matrix. Außerdem gilt  und damit ist
und damit ist  . Die Matrix
. Die Matrix  ist damit eine invertierbare Matrix. Die inverse Matrix zu A sieht dabei wie folgt aus
ist damit eine invertierbare Matrix. Die inverse Matrix zu A sieht dabei wie folgt aus
 .
.
Wie du die Inverse genau bestimmen kannst, erfährst du in unserem Video Inverse Matrix berechnen .
Meistens lohnt es sich, vorher kurz die Invertierbarkeit der Matrix zu überprüfen.
Hinweis: Übrigens, eine invertierbare Matrix nennt man regulär. Ist eine Matrix nicht invertierbar, so nennt man sie singulär.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Inverse Matrix Eigenschaften
Ist eine Matrix invertierbar, dann kannst du natürlich auch weiter mit ihr rechnen. Hier haben wir die wichtigsten Regeln und Eigenschaften für dich zusammengefasst.
Bei der Multiplikation von zwei Matrizen kannst du erst das Produkt bilden und davon die inverse Matrix bestimmen. Oder du multiplizierst gleich die inversen Matrizen, dann aber in umgekehrter Reihenfolge.
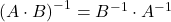
Ganz ähnlich funktioniert es, wenn du die Matrix mit einer Zahl  multiplizierst. Da brauchst du dann den Kehrwert
multiplizierst. Da brauchst du dann den Kehrwert  der Zahl
der Zahl  , also zum Beispiel
, also zum Beispiel  für
für  .
.

Eine inverse Matrix ist selbst wieder eine invertierbare Matrix. Und die Inverse der inversen Matrix ist wieder die ursprüngliche Matrix.
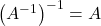
Du kannst eine inverse Matrix auch transponieren. Das Ergebnis ist das Gleiche, wie wenn du die Inverse einer transponierten Matrix bildest.

Bei einer orthogonalen Matrix sind die beiden sogar gleich.

Der Rang einer Matrix ändert sich nicht, es gilt also
 .
.
Und es gibt auch einen Zusammenhang zwischen der Determinante einer Matrix und der Determinante der inversen Matrix.

Lösung
Die Matrix  ist eine invertierbare Matrix, weil sie quadratisch ist und es gilt
ist eine invertierbare Matrix, weil sie quadratisch ist und es gilt
 .
.
