Vektorraum beweisen
Inhaltsübersicht
Koordinatenraum
Der wohl bekannteste Vektorraum ist der Koordinatenraum. Sei  ein Körper und
ein Körper und  eine natürliche Zahl. Dann ist der Koordinatenraum definiert als die Menge aller
eine natürliche Zahl. Dann ist der Koordinatenraum definiert als die Menge aller  -Tupel mit Einträgen aus
-Tupel mit Einträgen aus  :
:
 .
.
Dabei ist die Vektoraddition  für zwei Vektoren
für zwei Vektoren  und
und  aus
aus  folgendermaßen definiert:
folgendermaßen definiert:

mit  als Addition im Körper
als Addition im Körper  .
.
Die Skalarmultiplikation  ist für
ist für  als
als

festgelegt. Dabei stellt  die Multiplikation im Körper
die Multiplikation im Körper  dar.
dar.
Beispielsweise ist die euklidische Ebene  ein solcher Koordinatenraum.
ein solcher Koordinatenraum.
Wir wollen nun im Folgenden zeigen, dass es sich beim Koordinatenraum  tatsächlich um einen Vektorraum handelt, indem wir die Vektorraumaxiome prüfen. Hierfür seien
tatsächlich um einen Vektorraum handelt, indem wir die Vektorraumaxiome prüfen. Hierfür seien  Elemente aus
Elemente aus  und
und  und
und  aus
aus  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Axiome der Vektoraddition:
Zuerst müssen wir das Assoziativgesetz V1 zeigen. Wir betrachten daher  und führen die Vektoraddition entsprechend ihrer Definition aus:
und führen die Vektoraddition entsprechend ihrer Definition aus:


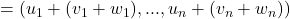 .
.
Da in jedem Körper  das Assoziativgesetz gilt, können wir nun entsprechend Umklammern und erhalten:
das Assoziativgesetz gilt, können wir nun entsprechend Umklammern und erhalten:




 .
.
Damit wurde V1 bewiesen.
Für V2 müssen wir zeigen, dass ein sogenanntes neutrales Element bezüglich der Addition im Vektorraum existiert. In diesem Fall ist es das  -Tupel,
welches in jedem Eintrag das Nullelement
-Tupel,
welches in jedem Eintrag das Nullelement  des Körpers
des Körpers  stehen hat:
stehen hat:

Wir müssen jedoch noch zeigen, dass es sich bei diesem Element tatsächlich um das neutrale Element von  handelt. Wir betrachten dafür
handelt. Wir betrachten dafür

Da  das Nullelement, also das neutrale Element der Addition in
das Nullelement, also das neutrale Element der Addition in  darstellt, gilt
darstellt, gilt  für alle
für alle  und deshalb
und deshalb

Völlig analog begründet sich auch  , womit V2 bewiesen ist.
, womit V2 bewiesen ist.
Für V3 müssen wir zeigen, dass jeder Vektor  ein inverses Element
ein inverses Element  im Vektorraum besitzt. Daher betrachten wir einen beliebigen Vektor
im Vektorraum besitzt. Daher betrachten wir einen beliebigen Vektor  , dessen Einträge bekanntermaßen alle aus dem Körper
, dessen Einträge bekanntermaßen alle aus dem Körper  stammen. Nun wissen wir zudem, dass zu jedem Element aus einem Körper ein additives Inverses in diesem Körper existiert. Somit gibt es für jedes der
stammen. Nun wissen wir zudem, dass zu jedem Element aus einem Körper ein additives Inverses in diesem Körper existiert. Somit gibt es für jedes der  ein additives Inverses
ein additives Inverses  , sodass
, sodass

gilt. Aus diesem Grund definieren wir das inverse Element in  als
als
 .
.
Denn damit ist



erfüllt. Analog gilt auch  und somit V3.
und somit V3.
Zum letzten Punkt der Vektoraddition V4: Die Kommutativität zwischen zwei Elementen  und
und 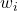 aus
aus  ist aufgrund der in
ist aufgrund der in  geltenden Kommutativität
geltenden Kommutativität

gegeben. Somit ist auch V4 erfüllt.
Axiome der Skalarmultiplikation
Im ersten Axiom S1 zeigen wir das Distributivgesetz. Hierfür berechnen wir

 .
.
Im Körper  ist das Distributivgesetz erfüllt, weshalb für
ist das Distributivgesetz erfüllt, weshalb für  und alle
und alle  in
in  gilt
gilt

Setzen wir das nun für jeden Eintrag oben ein, erhalten wir





und somit das Distributivgesetz.
Nun zum Axiom S2. Ähnlich zu S1 nutzt man hier aus, dass im Körper  gilt
gilt

Mit dieser Eigenschaft ergibt sich folglich:


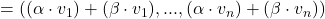


 .
.
S3 ist aufgrund der Assoziativität bzgl.  im Körper
im Körper  , erfüllt. Denn es gilt:
, erfüllt. Denn es gilt:



 .
.
Schließlich beweisen wir das letzte Vektorraumaxiom S4. Hierbei zeigen wir, dass das Einselement des Körpers  auch in der Skalarmultiplikation des Vektorraums ein neutrales Element darstellt. Nun, da
auch in der Skalarmultiplikation des Vektorraums ein neutrales Element darstellt. Nun, da  das neutrale Element der Multiplikation ist, d.h.
das neutrale Element der Multiplikation ist, d.h.  für alle
für alle  , gilt:
, gilt:
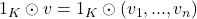


Somit haben wir bewiesen, dass der Koordinatenraum  ein Vektorraum ist.
ein Vektorraum ist.
Polynomräume
Ein weiteres sehr bekanntes Beispiel für einen Vektorraum ist die Menge der Polynome mit Koeffizienten aus einem Körper  :
:
![Rendered by QuickLaTeX.com \mathbb{K}[X] := \left\{p(x) = a_0 + a_1x+ a_2x^2 + a_3x^3 + ...+ a_nx^n | a_i \in \mathbb{K}, n \in \mathbb{N}\right\}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-22efc55c3057f00645f6418fc7337ec4_l3.png)
Das heißt jedes Polynom wird durch die Folge ihrer Koeffizienten charakterisiert. Dabei gilt für ein Polynom vom Grad  , dass die Folge der Koeffizienten
, dass die Folge der Koeffizienten  ab dem
ab dem  -ten Folgenglied nur aus Nullelementen
-ten Folgenglied nur aus Nullelementen  besteht, d.h.
besteht, d.h.  .
.
Die Vektoraddition entspricht in diesem Fall der üblichen Addition von Polynomen, d.h. für zwei Polynome  und
und  aus
aus ![Rendered by QuickLaTeX.com \mathbb{K}[X]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-079b518d7a2911a2666395363bff4b65_l3.png) gilt
gilt
 .
.
Die Skalarmultiplikation ist ebenfalls nicht überraschend für  als
als

definiert. Wir möchten auch für den Polynomraum zeigen, dass es sich tatsächlich um einen Vektorraum handelt, indem wir die Vektorraumaxiome prüfen.
Axiome der Vektoraddition
Es seien  und
und  Polynome aus
Polynome aus ![Rendered by QuickLaTeX.com \mathbb{K}[X]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-079b518d7a2911a2666395363bff4b65_l3.png) und
und  und
und  aus
aus  .
.
V1: Das Assoziativgesetz ist aufgrund der bereits geltenden Assoziativität im Körper  erfüllt. Daher gilt
erfüllt. Daher gilt
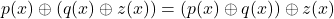 .
.
V2: Das neutrale Element ![Rendered by QuickLaTeX.com 0_{\mathbb{K}[X]}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6bb4052d11c6d6cd3994bb77a4d14492_l3.png) entspricht dem Nullpolynom, d.h. jenem Polynom, das durch die Nullfolge
entspricht dem Nullpolynom, d.h. jenem Polynom, das durch die Nullfolge  charakterisiert ist. Denn damit gilt
charakterisiert ist. Denn damit gilt
![Rendered by QuickLaTeX.com p(x) \oplus 0_{\mathbb{K}[X]} = \sum \limits_{i=0}^n (0_K+a_i)x^{i} = \sum \limits_{i=0}^n a_ix^{i} = p(x)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8747381a4f0b5c4b3f259b50e9858806_l3.png) ,
,
genauso wie ![Rendered by QuickLaTeX.com 0_{\mathbb{K}[X]} \oplus p(x) = p(x)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a600999b72a38b7c94cd762adb77f611_l3.png) .
.
V3: Zu jedem Polynom  existiert ein inverses Element
existiert ein inverses Element  , welches durch die additiven Inversen der Koeffizienten im Körper
, welches durch die additiven Inversen der Koeffizienten im Körper  definiert ist. D.h.
definiert ist. D.h.  mit
mit  für alle
für alle  . Denn so ist die Eigenschaft
. Denn so ist die Eigenschaft
![Rendered by QuickLaTeX.com p(x) \oplus p(x)^{-1} = \sum \limits_{i=0}^n (a_i +(-a_i))x^{i}= \sum \limits_{i=0}^n 0_K x^{i} = 0_{\mathbb{K}[X]}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-02d8e2032acaa4e8b600fbb02e910750_l3.png)
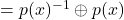
erfüllt.
V4: Das Kommutativgesetz ist ebenfalls aufgrund der in  geltenden Kommutativität gegeben. Demnach gilt
geltenden Kommutativität gegeben. Demnach gilt
 .
.
Axiome der Skalarmultiplikation
S1: Das Distributivgesetz gilt erneut aus dem Grund, dass die Distributivität in  erfüllt ist und somit:
erfüllt ist und somit:


 .
.
S2: Da die gewünschte Eigenschaft in  gilt, erhalten wir auch im Polynomraum
gilt, erhalten wir auch im Polynomraum




S3:  besitzt die Assoziativität auch bzgl. der in
besitzt die Assoziativität auch bzgl. der in  definierten Mutiplikation. Diese wenden wir an, um S3 zu zeigen:
definierten Mutiplikation. Diese wenden wir an, um S3 zu zeigen:




S4: Wir berechnen die Skalarmultiplikation  , wobei
, wobei  das neutrale Element der Multiplikation in
das neutrale Element der Multiplikation in  darstellt:
darstellt:



Damit sind schließlich alle Vektorraumaxiome erfüllt.
Funktionenräume
Eine weitere große Gruppe von Vektorräumen sind die Funktionenräume. Um einen Funktionenraum definieren zu können, benötigen wir einen Körper  , einen Vektorraum
, einen Vektorraum  über diesen Körper und eine beliebige Menge
über diesen Körper und eine beliebige Menge  . Dann entspricht der Funktionenraum
. Dann entspricht der Funktionenraum 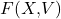 der Menge aller Funktionen
der Menge aller Funktionen
 .
.
Die Vektoraddition für den Funktionenraum muss demnach zwei Funktionen, die von  nach
nach  abbilden, erneut auf eine Funktion mit Definitionsmenge
abbilden, erneut auf eine Funktion mit Definitionsmenge  und Zielmenge
und Zielmenge  abbilden.
abbilden.
Deshalb definieren wir  , als die Funktion
, als die Funktion  mit der Abbildungsvorschrift:
mit der Abbildungsvorschrift:
 .
.
Mit 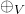 als die auf
als die auf  definierte Vektoraddition und
definierte Vektoraddition und  und
und  als Elemente in
als Elemente in  , liegt das Bild von
, liegt das Bild von  in
in  und ist demnach wohldefiniert.
und ist demnach wohldefiniert.
Analog definieren wir auch die Skalarmultiplikation von 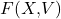 . Für
. Für  und
und  ist
ist  die Funktion, welche alle
die Funktion, welche alle  folgendermaßen abbildet:
folgendermaßen abbildet:
 .
.
Basis und Dimension eines Vektorraums
In diesem Abschnitt erklären wir dir, was es mit der Basis und der Dimension eines Vektorraums auf sich hat.
Basis
Vektoren  eines Vektorraums
eines Vektorraums  über
über  bilden eine Basis, wenn sie linear unabhängig sind und den gesamten Vektorraum aufspannen. Damit ist gemeint, dass jedes Element des Vektorraums als eine Linearkombination
bilden eine Basis, wenn sie linear unabhängig sind und den gesamten Vektorraum aufspannen. Damit ist gemeint, dass jedes Element des Vektorraums als eine Linearkombination

der Basisvektoren  mit Koeffizienten
mit Koeffizienten  aus
aus  im Vektorraum dargestellt werden kann.
im Vektorraum dargestellt werden kann.
Beispielsweise sind die Vektoren

eine sogenannte Standardbasis der Euklidischen Ebene  . Denn sie sind linear unabhängig und jeder Vektor
. Denn sie sind linear unabhängig und jeder Vektor  kann einfach mit
kann einfach mit  und
und  als Linearkombination
als Linearkombination

im Vektorraum dargestellt werden. Tatsächlich handelt es sich bei dieser Basis sogar um eine sogenannte Orthonormalbasis .
Dimension
Als Dimension bezeichnet man die Anzahl der Basisvektoren einer Basis des Vektorraums. Tatsächlich muss diese Anzahl nicht wie im obigen Beispiel immer endlich sein. Betrachten wir noch einmal den Polynomraum ![Rendered by QuickLaTeX.com \mathbb{K}[X]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-079b518d7a2911a2666395363bff4b65_l3.png) , also die Menge aller Polynome mit Koeffizienten aus
, also die Menge aller Polynome mit Koeffizienten aus  . Für diesen Vektorraum stellt
. Für diesen Vektorraum stellt

eine Basis des Vektorraums dar. Diese Menge ist unendlich, weshalb auch die Dimension des Polynomraums unendlich ist.
Vektorräume mit zusätzlicher Struktur
Oftmals reichen die Vektoraddition und Skalarmultiplikation nicht aus und man möchte mehr Struktur auf dem Vektorraum haben, beispielsweise um Abstände zwischen zwei Elementen betrachten zu können. Es folgt eine Reihe von Vektorräumen mit solch zusätzlicher Struktur.
Normierter Raum
Das ist ein Vektorraum, dessen Vektoren eine Länge, die sogenannte Norm, besitzen.
Prähilbertraum
Ein Prähilbertraum ist ein Vektorraum über den reellen oder komplexen Zahlen mit einer zusätzlichen Verknüpfung, die das Betrachten von Längen und Winkeln im Vektorraum ermöglicht.
Euklidischer Vektorraum
Der euklidische Vektorraum entspricht dem Prähilbertraum über  . Die zusätzliche Verknüpfung ist in diesem Fall das Skalarprodukt.
. Die zusätzliche Verknüpfung ist in diesem Fall das Skalarprodukt.
Unitärer Vektorraum
Dieser ist ebenfalls ein Spezialfall des Prähilbertraums, hier mit  . Die zusätzliche Verknüpfung entspricht dem Skalarprodukt in
. Die zusätzliche Verknüpfung entspricht dem Skalarprodukt in  .
.
%MCEPASTEBIN%
