Matrix diagonalisieren
Das Matrix Diagonalisieren vereinfacht viele Aufgaben, die Matrizen enthalten. Hier zeigen wir dir, wie du eine Matrix diagonalisieren kannst und wann eine Matrix diagonalisierbar ist. Schaue dir auch unser passendes Video an!
Inhaltsübersicht
Diagonalmatrix einfach erklärt
Wenn du eine quadratische Matrix diagonalisierst, machst du aus einer nicht diagonalen Matrix eine Diagonal Matrix.
![Rendered by QuickLaTeX.com \[ \mathbf{A}={\begin{pmatrix} 2 & 1 & 1 \\ 0 & 3 & 0 \\ 0 & 2 & 4 \end{pmatrix}} \longrightarrow \mathbf{D_A} = \begin{pmatrix} \textcolor{blue}{2} &0 &0 \\ 0 & \textcolor{blue}{3} & 0 \\ 0 & 0 & \textcolor{blue}{4} \end{pmatrix} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2c734677254d68fc61204dc8a76d1068_l3.png)
Eine Diagonalmatrix ist eine besondere quadratische und symmetrische Matrix. Sie enthält Einträge ungleich 0 nur auf der Hauptdiagonalen. Alle anderen Matrixelemente sind gleich 0. Beispiele:
![Rendered by QuickLaTeX.com \[ \begin{pmatrix}\textcolor{blue}{4} & 0 \\ 0 & \textcolor{blue}{-3} \end{pmatrix} \qquad \begin{pmatrix}\textcolor{blue}{1} & 0 & 0 \\ 0 & \textcolor{blue}{4} & 0 \\ 0 & 0& \textcolor{blue}{0}\end{pmatrix} \qquad \begin{pmatrix}\textcolor{blue}{-12} & 0 & 0 \\ 0 & \textcolor{blue}{-653} & 0 \\ 0 & 0& \textcolor{blue}{34}\end{pmatrix} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-adb37262c738ff25371b0067c790a2f8_l3.png)
Eine Diagonalmatrix hat einige praktische Eigenschaften:
- die Determinante ist der Produkt der Einträge auf der Hauptdiagonalen. (det(A) = det(DA) = 2 • 3 • 4 = 24)
- der Rang der Matrix ist gleich der Nichtnull-Zeilen. (rang(A) = 3)
- die Eigenwerte sind die Einträge der Hauptdiagonalen mit den Einheitsvektoren als Eigenvektoren.
Das Matrix-Diagonalisieren erleichtert dir außerdem viele Rechenaufgaben:
- Matrixmultiplikationen (Matrizenmultiplikation)
- Skalarmultiplikation
- Matrixaddition und Matrixsubtraktion
- Inverse Matrix berechnen
- Transponierte Matrix berechnen
Wann ist eine Matrix diagonalisierbar?
Du kannst aber nicht jede Matrix diagonalisieren. Wie kannst du die Diagonalisierbarkeit einer Matrix prüfen?
Eine 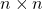 -Matrix ist diagonalisierbar, wenn
-Matrix ist diagonalisierbar, wenn
- sie quadratisch ist,
- ihr charakteristisches Polynom n Nullstellen hat und
- die geometrische Vielfachheit und die algebraische Vielfachheit ihrer Eigenwerte gleich sind.
Was das genau bedeutet, schaust du dir am besten an zwei Beispielen an.
Beispiel 1: Charakteristisches Polynom finden
Du kannst deine n x n-Matrix diagonalisieren, wenn ihr charakteristisches Polynom 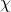 genau n Nullstellen hat. Wie viele Nullstellen hat das charakteristisches Polynom der 3 x 3-Matrix M?
genau n Nullstellen hat. Wie viele Nullstellen hat das charakteristisches Polynom der 3 x 3-Matrix M?
![Rendered by QuickLaTeX.com \[ \mathbf{M}=\textcolor{blue}{\begin{pmatrix} 2 & 4 & 0 \\ -4 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fe5f23e312149b9911341bd4ba8a4242_l3.png)
Schritt 1: Als Erstes musst du das charakteristische Polynom berechnen. Dafür schreibst du die Variable 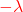 in die Hauptdiagonale deiner Matrix. Anschließend musst du ihre Determinante berechnen
.
in die Hauptdiagonale deiner Matrix. Anschließend musst du ihre Determinante berechnen
.
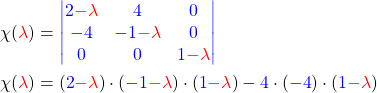
Schritt 2: Um die Diagonalisierbarkeit prüfen zu können, musst du die Nullstellen
von deinem charakteristischen Polynom finden. Diese Nullstellen nennst du auch Eigenwerte. Um die Eigenwerte berechnen
zu können, zerlegst du das Polynom in Linearfaktoren. Als erstes klammerst du daher 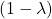 aus.
aus.
![Rendered by QuickLaTeX.com \[ \chi(\textcolor{red}{\lambda}) =(\textcolor{blue}{1}\textcolor{red}{-\lambda}) \cdot [ (\textcolor{blue}{2}\textcolor{red}{-\lambda}) \cdot (\textcolor{blue}{-1}\textcolor{red}{-\lambda}) - \textcolor{blue}{4}\cdot (\textcolor{blue}{-4}) ] \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-503240d3352cfa4797aaebd2c57bda20_l3.png)
Danach multiplizierst du aus und fasst die Terme zusammen.
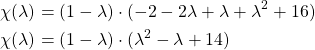
Das charakteristische Polynom hat also nur eine reelle Nullstelle bei 1. Die zweite Klammer 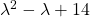 wird nie null.
wird nie null.
Fazit: Die Matrix M hat 3 Reihen und Spalten, aber ihr charakteristisches Polynom hat nur 1 Nullstelle. Du hast also zu wenig Nullstellen und deine Matrix ist nicht diagonalisierbar.
Beispiel 2: Vielfältigkeit der Eigenwerte bestimmen
Ist diese Matrix diagonalisierbar?
![Rendered by QuickLaTeX.com \[ \mathbf{M}=\textcolor{blue}{\begin{pmatrix} 3 & 2 & 3 \\ 4 & 7 & 9 \\ -3 & -4 & -5 \end{pmatrix}} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e0d734aa1f492377c2155377cf4c4452_l3.png)
Schritt 1: Finde das charakteristischen Polynom.
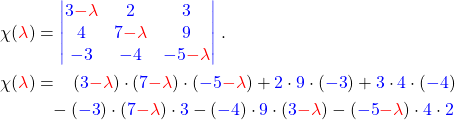
Schritt 2: Danach vereinfachst du die Terme und bekommst
![Rendered by QuickLaTeX.com \[\chi(\lambda) = -(\lambda-2)^2\cdot (\lambda-1) .\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3c46378abe638de7c9325a99749c22a1_l3.png)
Hier sind die Nullstellen bei 2 (doppelt) und 1 (einfach). Damit hast du insgesamt drei Nullstellen des charakteristischen Polynoms, also drei Eigenwerte. Die erste Bedingung der Diagonalisierbarkeit einer Matrix ist erfüllt.
Wie sieht es mit der zweiten Bedingung aus? Die geometrische Vielfachheit der Eigenwerte muss gleich der algebraischen Vielfachheit der Eigenwerte sein.
Die geometrische Vielfachheit ist gleich der algebraischen Vielfachheit,
- wenn du einen einfachen Eigenwert hast und genau ein Eigenvektor dazu gehört,
- wenn du einen quadratischen Eigenwert hast und genau zwei Eigenvektoren dazu gehören,
- usw.
Schritt 3: Du musst also die Eigenvektoren berechnen . Du kannst für deine Eigenwerte folgende Eigenvektoren ausrechnen:
![Rendered by QuickLaTeX.com \[ \lambda_1 = 1 \longrightarrow v_1 = \begin{pmatrix}0\\-3\\2\end{pmatrix} \quad\text{und}\quad \lambda_2 = 2 \longrightarrow v_2 = \begin{pmatrix}-1\\-1\\1\end{pmatrix} . \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-03d0293535f76caafcf6118c33f27043_l3.png)
Du hast für jeden Eigenwert einen Eigenvektor. Die entsprechenden Eigenräume haben also eine geometrische Vielfachheit von 1. Dein zweiter Eigenwert (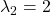 ) ist aber eine doppelte Nullstelle. Er hat also eine algebraische Vielfachheit von 2.
) ist aber eine doppelte Nullstelle. Er hat also eine algebraische Vielfachheit von 2.
Fazit: Die geometrische Vielfachheit ist ungleich der algebraischen Vielfachheit. Deine Matrix ist nicht diagonalisierbar.
Matrix diagonalisieren
Das Matrixdiagonalisieren funktioniert ähnlich wie die Diagonalisierbarkeit zu prüfen.
Um eine Matrix zu diagonalisieren,
- berechnest du die Eigenwerte,
- ihre Eigenvektoren, um die Diagonalisierbarkeit zu prüfen, und
- stellst die Diagonalmatrix auf.
Schauen wir uns jetzt an zwei Beispielen an, wie du mit deinen Eigenwerten die Diagonalmatrix berechnen kannst.
Beispiele
Wie lautet die Diagonalmatrix der diagonalisierbaren Matrix A?
![Rendered by QuickLaTeX.com \[ \mathbf{A}=\textcolor{blue}{\begin{pmatrix} 2 & 1 & 1 \\ 0 & 3 & 0 \\ 0 & 2 & 4 \end{pmatrix}} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-42e67010992f9208d84e6fbf46c4c067_l3.png)
Schritt 1: Finde das charakteristische Polynom 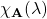 !
!
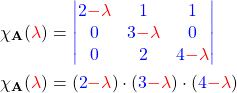
Hier kannst du die Eigenwerte direkt ablesen:
![Rendered by QuickLaTeX.com \[\lambda_1 = 2 \text{, }\lambda_2 = 3 \text{ und } \lambda_3 = 4 .\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d71bf8b8ed0022038661e2148773656d_l3.png)
Schritt 2: Jetzt müsstest du die Diagonalisierbarkeit prüfen. Die Aufgabenstellung sagt dir allerdings schon, dass die Matrix diagonalisierbar ist.
Schritt 3: Zuletzt musst du mit deinen Eigenwerten die Diagonalmatrix DA schreiben. Dafür schreibst du deine Eigenwerte auf die Hauptdiagonale einer Matrix. In welcher Reihenfolge du die Eigenwerte in deine Diagonalmatrix schreibst, ist egal. Eine mögliche Diagonalisierung ist
![Rendered by QuickLaTeX.com \[ \mathbf{D_A} = \begin{pmatrix} \textcolor{red}{\lambda_1} &0 &0 \\ 0 & \textcolor{red}{\lambda_2} & 0 \\ 0 & 0 & \textcolor{red}{\lambda_3} \end{pmatrix} = \begin{pmatrix} \textcolor{red}{2} &0 &0 \\ 0 & \textcolor{red}{3} & 0 \\ 0 & 0 & \textcolor{red}{4} \end{pmatrix} . \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a383809b5259388fc37a6485252431ab_l3.png)
Geschafft! Wie wäre es mit einem zweiten Beispiel?
Beispiel 2: Wie lautet die Diagonalmatrix der diagonalisierbaren Matrix B?
![Rendered by QuickLaTeX.com \[ \mathbf{B}=\textcolor{blue}{\begin{pmatrix} 3 & 2 & -2 \\ -1 & 0 & 2 \\ 0 & 0 & -1 \end{pmatrix}} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3431fd765394cb330ea837787c221297_l3.png)
Schritt 1: Finde das charakteristische Polynom 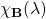 !
!
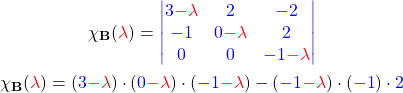
Du kannst 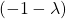 ausklammern und den Rest zusammenfassen. Dann bekommst du das charakteristische Polynom
ausklammern und den Rest zusammenfassen. Dann bekommst du das charakteristische Polynom
![Rendered by QuickLaTeX.com \[ \chi_{\mathbf{B}}(\lambda) = (-1-\lambda) \cdot (\lambda^2 -3\lambda + 2) .\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9022e9ed0ed0951768116d9bd59f3a47_l3.png)
Hier kannst du den ersten Eigenwert ablesen und die anderen beiden mit der pq-Formel berechnen:
![Rendered by QuickLaTeX.com \[\lambda_1 = -1 \text{, }\lambda_2 = 1 \text{ und } \lambda_3 = 2 .\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-315f574e793aa9e4a84d0cb01f0e0824_l3.png)
Schritt 2: Jetzt müsstest du die Diagonalisierbarkeit prüfen. Die Aufgabenstellung sagt dir allerdings schon, dass die Matrix diagonalisierbar ist.
Schritt 3: Zuletzt musst du mit deinen Eigenwerten die Diagonalmatrix DB schreiben:
![Rendered by QuickLaTeX.com \[ \mathbf{D_B} = \begin{pmatrix} \lambda_1 &0&0\\ 0&\lambda_2&0\\ 0&0&\lambda_3 \end{pmatrix} = \begin{pmatrix} -1 &0&0\\ 0&1&0\\ 0&0&2 \end{pmatrix} . \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ced607dd242ee1389eb03bdb1e42437e_l3.png)
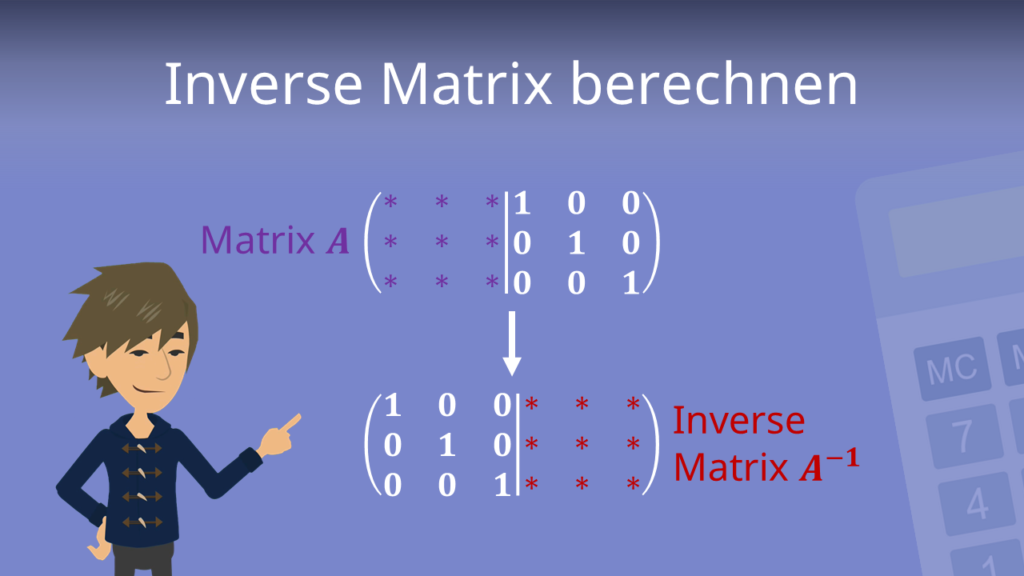
Inverse Matrix
Von einer Diagonalmatrix lässt sich ganz einfach eine inverse Matrix finden. Wenn du deine Diagonalmatrix mit ihrer inversen Matrix multiplizierst, bekommst du die Einheitsmatrix. Schaue dir am besten unser Video dazu an!
![Rendered by QuickLaTeX.com \[ \textcolor{red}{ \begin{pmatrix}2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 6\end{pmatrix} } \cdot \textcolor{blue}{ \begin{pmatrix}\frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{-1} & 0 \\ 0 & 0 & \frac{1}{6}\end{pmatrix} } = \textcolor{olive}{ \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} } \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-327b604c0852f95a03a8f64c8a5125c3_l3.png)