Video

Quiz

Hier geht's zum Video „Vollständige Induktion“

Vollständige Induktion Aufgaben

Hier zeigen wir einige vollständige Induktion Aufgaben Schritt für Schritt! Du willst dich lieber entspannt zurücklehnen? Dann schau dir unser Video an.

Wir haben auch zur vollständigen Induktion ein Video für dich. Schau es dir an! Dort erklären wir dir Schritt für Schritt, wie du einen Beweis durchführst.

Inhaltsübersicht

Vollständige Induktion Aufgabe 1

Summe über Quadratzahlen: Zeige, dass für alle natürlichen Zahlen gilt

$\(\sum \limits_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}$ .

Lösung 1

Induktionsanfang:

Zuerst überprüfst du die Formel für n=1 . Dafür kannst du den Startwert einfach einsetzen.

$\(\sum \limits_{k=1}^1 k^2 = 1^2 = 1$

$\frac{1 \cdot (1+1) \cdot (2 \cdot 1+1)}{6}=\frac{1 \cdot 2 \cdot 3}{6}=\frac{6}{6} = 1$

Die linke und rechte Seite der Gleichung liefern das gleiche Ergebnis, die Formel stimmt also.

Induktionsvoraussetzung:

Gelte $\(\sum \limits_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6}$ für beliebiges $n \in \mathbb{N}$ .

Induktionsbehauptung:

Dann gilt für n+1

$\(\sum \limits_{k=1}^{n+1} k^2 = \frac{(n+1)((n+1)+1)(2(n+1)+1)}{6}$ .

Induktionsschluss:

Und jetzt geht es los mit dem eigentlichen Beweis und den Umformungen.

$\(\sum \limits_{k=1}^{n+1} k^2 = \(\sum \limits_{k=1}^n k^2 + \left(n+1\right)^2$

Ziehe den letzten Summanden heraus und setze die Induktionsvoraussetzung ein.

$=\frac{n(n+1)(2n+1)}{6} + n^2+2n+1 = \frac{2n^3+3n^2+n}{6} + \frac{6n^2+12n+6}{6}=$

$=\frac{2n^3+9n^2+13n+6}{6} = \frac{(n+1)(n+2)(2n+3)}{6} = \frac{(n+1)((n+1)+1)(2(n+1)+1)}{6}$

Danach musst du eigentlich nur noch ausmultiplizieren und geschickt zusammenfassen.

Vollständige Induktion Aufgabe 2

Summe über ungerade Zahlen: Beweise, dass für alle $n \in \mathbb{N}$ gilt

$\(\sum \limits_{k=1}^n (2k-1) = n^2$ .

Lösung 2

Induktionsanfang:

Hier zeigst du erstmal, dass die Formel für die kleinste ungerade Zahl gilt, nämlich für n=1 .

$\(\sum \limits_{k=1}^1 2 \cdot 1 - 1 = 1$

1^2 = 1

Nach dem Einsetzen stimmen die linke und die rechte Seite der Formel wieder überein.

Induktionsvoraussetzung:

Sei $\(\sum \limits_{k=1}^n (2k-1) = n^2$ für ein beliebiges $n \in \mathbb{N}$ .

Induktionsbehauptung:

Dann gilt für n+1

$\(\sum \limits_{k=1}^{n+1} 2k-1 = (n+1)^2$ .

Induktionsschluss:

Und genau das rechnest du jetzt einmal nach.

$\(\sum \limits_{k=1}^{n+1} 2k-1 = \(\sum \limits_{k=1}^n (2k-1) + (2(n+1)-1)$

Auch hier ist der erste Schritt wieder das Herausziehen des letzten Summanden, damit du die Induktionsvoraussetzung benutzen kannst.

= n^2 + (2n+2-1) = n^2 +2n+1 = (n+1)^2

Dank der binomischen Formeln ist die Umformung hier recht einfach. Schlussendlich hast du damit bewiesen, dass die Formel $\(\sum \limits_{k=1}^n (2k-1) = n^2$ für alle natürlichen Zahlen gilt.

Vollständige Induktion Aufgabe 3

Summe über Kubikzahlen: Zeige, dass für alle natürlichen Zahlen gilt

$\(\sum \limits_{k=1}^n k^3 = \frac{n^2(n+1)^2}{4}$ .

Lösung 3

Induktionsanfang:

Wie immer startest du mit dem Überprüfen der Aussage für n=1.

$\(\sum \limits_{k=1}^1 k^3 = 1^3 = 1$

$\frac{1^2 \cdot (1+1)^2}{4} = \frac{4}{4} = 1$

Die Ergebnisse der linken und rechten Seite der Formel sind wieder gleich, die Aussage stimmt.

Induktionsvoraussetzung:

Es gelte $\(\sum \limits_{k=1}^n k^3 = \frac{n^2(n+1)^2}{4}$ für ein beliebiges $n \in \mathbb{N}$ .

Induktionsbehauptung:

Dann gilt für n+1

$\(\sum \limits_{k=1}^{n+1} k^3 = \frac{(n+1)^2((n+1)+1)^2}{4}$ .

Induktionsschluss:

Und auch das beweist du jetzt durch Nachrechnen.

$\(\sum \limits_{k=1}^{n+1} k^3 = \(\sum \limits_{k=1}^n k^3 + (n+1)^3$

Nach dem Abspalten des letzten Summanden kannst du wieder die Formel für n benutzen.

$= \frac{n^2(n+1)^2}{4} + n^3+3n^2+3n+1=\frac{n^4+2n^3+n^2}{4} + \frac{4n^3+12n^2+12n+4}{4}=$

$=\frac{n^4+6n^3+13n^2+12n+4}{4} = \frac{(n^2+2n+1)(n^2+4n+4)}{4} = \frac{(n+1)^2(n+2)^2}{4}$ .

Schlussendlich fasst du nur noch die Rechnung zusammen und landest bei der rechten Seite der Formel für n+1. Also gilt tatsächlich für alle natürlichen Zahlen

$\(\sum \limits_{k=1}^n k^3 = \frac{n^2(n+1)^2}{4} = \left(\frac{n(n+1)}{2}\right)^2$ .

Vollständige Induktion Aufgabe 4

im Videozur Stelle im Video springen

Ungleichung: Zeige, dass für alle natürlichen Zahlen $n \geq 2$ gilt

2^n > n+1 .

Lösung 4

Induktionsanfang:

Achtung, hier musst du zeigen, dass die Formel für n=2 gilt! Denn das ist die kleinste Zahl, für die die Ungleichung gelten soll.

2^2 = 4 und 2+1=3

4>3

Nach Einsetzen der 2 kannst du schnell feststellen, dass die Ungleichung gilt.

Induktionsvoraussetzung:

Es gelte 2^n>n+1 für eine beliebige natürliche Zahl $n \geq 2$ .

Induktionsbehauptung:

Dann gilt für n+1

$2^{n+1} > (n+1)+1$ .

Induktionsschluss:

Und auch das rechnest du jetzt wieder nach. Starte auf der linken Seite der Ungleichung.

$2^{n+1} = 2^n \cdot 2$

Hier ist wieder der erste Schritt, den gegebenen Term auf 2^n zurückzuführen. Diesmal funktioniert das mit den Potenzgesetzen. Das kannst du mit Hilfe der Induktionsvoraussetzung abschätzen.

$2 \cdot 2^n > 2 \cdot (n+1)= 2n+2>n+2=(n+1)+1$

Damit hast du gezeigt, dass $2^{n+1} > (n+1)+1$ . Deshalb gilt die Ungleichung für alle natürlichen Zahlen $n \geq 2$ .

Vollständige Induktion Aufgabe 5

Teilbarkeit: Zeige, dass für alle natürlichen Zahlen n^2+n gerade ist.

Lösung 5

Induktionsanfang:

Je nachdem, ob die Null für dich zu den natürlichen Zahlen gehört oder nicht, startest du entweder bei n=0 oder bei n=1 .

Für n=0 gilt 0^2+0=0 und 0 ist gerade.

Für n=1 gilt 1^2+1=2 und 2 ist ebenfalls gerade.

In beiden Fällen hast du den Anfang geschafft. Jetzt kommt der Induktionsschritt.

Induktionsvoraussetzung:

Es gelte also die Aussage „ n^2+n ist gerade“ für ein beliebiges n.

Induktionsbehauptung:

Dann gilt für n+1 die Aussage „ (n+1)^2+(n+1) ist ebenfalls gerade“.

Induktionsschluss:

Das musst du jetzt nur noch beweisen. Starte bei der Aussage für n+1.

$(n+1)^2 + (n+1) = n^2+2n+1+n+1 = n^2+n+2n+2=(n^2+n)+2 \cdot (n+1)$

Durch Umformung hast du den Term so aufgeteilt, dass du Aussagen über die einzelnen Summanden machen kannst. n^2+n ist gerade, das hast du so in der Induktionsannahme festgehalten. $2 \cdot (n+1)$ enthält den Faktor 2 und ist deshalb ebenfalls gerade.

Also ist 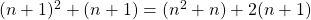(n+1)^2+(n+1) = (n^2+n)+2(n+1) gerade und die Aussage gilt für alle natürlichen Zahlen.

zur Videoseite: Vollständige Induktion Aufgaben

Gaußsche Summenformel

Geometrische Summenformel

Vollständige Induktion

Vollständige Induktion Aufgaben

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .