Kurvendiskussion Aufgaben
Kurvendiskussionen können am Anfang sehr unübersichtlich sein, aber keine Bange! Hier rechnen wir mit dir eine vollständige Kurvendiskussion aus. Schau dir auch unser passendes Video an!
Inhaltsübersicht
Kurvendiskussion einfach erklärt
Schau‘ dir zum Beispiel die ganzrationale Funktion  an. Die wichtigen Schritte in deiner Kurvendiskussion sind folgende:
an. Die wichtigen Schritte in deiner Kurvendiskussion sind folgende:
- Definitionsbereich bestimmen (Definitionslücken)
- y-Achsenabschnitt berechnen
- x-Achsenabschnitte berechnen (Nullstellen)
- Verhalten im Unendlichen (Grenzverhalten/ Limes)
- Symmetrieverhalten bestimmen (Punkt- oder Achsensymmetrie)
- Extrempunkte berechnen (Hochpunkte und Tiefpunkte)
- Monotonieverhalten bestimmen (Steigungsverhalten)
- Wendepunkte berechnen (Links-Rechts- und Rechts-Links-Punkte)
- Krümmungsverhalten bestimmen (Zweite Ableitung)
- Wertebereich bestimmen (Wertemenge)
- Funktionsgraph zeichnen
Später brauchst du die erste, zweite und dritte Ableitung
. Es lohnt sich, die Funktion vorher abzuleiten. Dafür brauchst du bei ganzrationalen Funktionen nur die Potenzregel
: 
– Gegebene Funktion: 
– 1. Ableitung: 
– 2. Ableitung: 
– 3. Ableitung: 
Definitionsbereich ermitteln
Die Definitionsmenge ist die Antwort auf die Frage: Welche x-Werte darfst du in die Funktion einsetzen?
Der erste Schritt in jeder Kurvendiskussion ist das Ermitteln der Definitionsmenge. Bei ganzrationalen Funktionen ist die Definitionsmenge  immer gleich der Menge der reellen Zahlen
immer gleich der Menge der reellen Zahlen  .
.
![Rendered by QuickLaTeX.com \[ \mathbb{D}_f = \mathbb{R} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-162790c80b735918431fcf3a8324f3c7_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
y-Achsenabschnitt berechnen
Der y-Achsenabschnitt ist der Schnittpunkt mit der y-Achse. Du findest ihn, indem du x=0 in deine Funktion einsetzt.
![Rendered by QuickLaTeX.com \[ y = f(0) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2689b2f78829d6e0541950ca85e304c4_l3.png)
Was ergibt das für deine Beispielfunktion?

Dein Graph schneidet die y-Achse in dem Punkt (0|4).
Nullstellen berechnen
Natürlich kann dein Funktionsgraph auch die x-Achse schneiden. Das sind die Nullstellen . Um sie zu finden, setzt du die Funktion gleich 0.
![Rendered by QuickLaTeX.com \[ f(x) \overset{!}{=} 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5a979841c95410e375577ccee0da77e6_l3.png)
Wann wird deine Beispielfunktion gleich 0?
![Rendered by QuickLaTeX.com \[ x^3 - 3x^2 + 4 \overset{!}{=} 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b3d91dc87b94c35a074270aa6ee8e340_l3.png)
Hier kannst du die erste Nullstelle erraten. Gute Kandidaten sind meistens 0, 1, -1, 2, -2. Durch den Schritt vorher weißt du, dass x=0 keine Nullstelle sein kann. Probiere als nächstes x=-1:
![Rendered by QuickLaTeX.com \[ f(\textcolor{red}{-1}) = (\textcolor{red}{-1})^3 - 3\cdot (\textcolor{red}{-1})^2 + 4 = -1 -3 \cdot 1 + 4 = -4+4 = 0 \;\textcolor{olive}{\checkmark} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c9d950fd0fe98de76fe4f1a8a23b4bf4_l3.png)
Deine erste Nullstelle ist tatsächlich bei x1=-1. Jetzt kannst du eine Polynomdivision rechnen, damit du die restlichen Nullstellen schneller finden kannst. Wenn du dir die Polynomdivision noch einmal anschauen magst, haben wir dir dafür ein Video vorbereitet.
![Rendered by QuickLaTeX.com \[ \begin{array}{l} \phantom{-}(x^3-3x^2+4) : (x+1) = x^2 - 4x + 4 \\ \underline{-(x^3+\phantom{3}x^2)} \\ \phantom{-(x^3}-4x^2 +4 \\ \phantom{x^{13}}\underline{- ( - 4x^2-4x)} \\ \phantom{-(x^{13}-4x^2-}4x + 4 \\ \phantom{-(x^3-3x^2}\underline{-(4x + 4)} \\ \phantom{-(x^3-3x^2-(4x + }0 \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-35397c0f2e5f682dfd91ea5801bf8ca8_l3.png)
Deine Funktion kannst du also auch so schreiben: 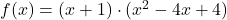 . Warum hilft dir die Polynomdivision? Ein Produkt ist gleich 0, wenn einer der Faktoren 0 ist. Die restlichen Nullstellen findest du deshalb mit dem Ansatz:
. Warum hilft dir die Polynomdivision? Ein Produkt ist gleich 0, wenn einer der Faktoren 0 ist. Die restlichen Nullstellen findest du deshalb mit dem Ansatz:
![Rendered by QuickLaTeX.com \[ x^2 -4x +4 \overset{!}{=} 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-79dcc0cbef4f128a2d4623e5c4913d69_l3.png)
Weil das eine quadratische Gleichung ist, kannst du sie mit der Mitternachtsformel oder der pq-Formel lösen.

Für die letzten beiden Nullstellen bekommst du dasselbe Ergebnis heraus. Es ist also eine doppelte Nullstelle.
Fazit: Deine Funktion hat eine einfache Nullstelle bei x1=-1 und eine doppelte Nullstelle bei x2=2. Die Punkte (-1|0) und (2|0) sind also die Schnittstellen des Funktionsgraphen mit der y-Achse.
Verhalten im Unendlichen bestimmen
Als Nächstes kümmerst du dich um das Grenzwertverhalten deiner Funktion. Das geht bei ganzrationalen Funktionen sehr schnell. Dafür schaust du dir den Term mit dem größten Exponenten an, den sogenannte Leitterm. Wenn sein Exponent gerade ist, geht die Funktion wie eine Parabel für kleine und große Zahlen gegen plus unendlich. Ist er ungerade, geht sie wie eine Gerade von minus unendlich nach plus unendlich. Falls der Term ein negatives Vorzeichen ist, geht die Funktion von plus unendlich nach minus unendlich.
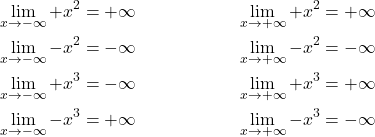
Hier ist der Leitterm x3. Du hast also einen ungeraden Exponenten mit positiven Vorzeichen. Dein Funktionsgraph kommt also von negativ unendlich und geht nach positiv unendlich.

Symmetrieverhalten bestimmen
Das Symmetrieverhalten ermittelst du, indem du -x in deine Funktion einsetzt.
Achsensymmetrie
zur y-Achse: 
Punktsymmetrie
zum Ursprung: 
Mit deiner Beispielfunktion sieht es dann so aus:
![Rendered by QuickLaTeX.com \[ f(-x) = (-x)^3 - 3(-x)^2 + 4 = -x^3 -3x^2 +4 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-83c81920117d470d7c04f66050a7dcc8_l3.png)
Wenn du dein Ergebnis mit der ursprünglichen Funktion  vergleichst, siehst du:
vergleichst, siehst du:
![Rendered by QuickLaTeX.com \[ f(-x) \neq f(x) \qquad f(-x) \neq -f(x) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e7785926aeac9b659060e31690b0c7f2_l3.png)
Fazit: Dein Funktionsgraph ist also weder symmetrisch zur y-Achse noch zum Ursprung.
Extrempunkte berechnen
Spätestens jetzt musst du die Ableitungen von f ausrechnen.
An Hochpunkten
gilt:  und
und 
An Tiefpunkten
gilt:  und
und 
1. Nullstelle der ersten Ableitung
Wegen der notwendigen Bedingung  musst du als erstes die Nullstellen der ersten Ableitung finden.
musst du als erstes die Nullstellen der ersten Ableitung finden.
![Rendered by QuickLaTeX.com \[ f'(x) = 3x^2 -6x \overset{!}{=} 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-473dec129a6aaeb9ed93cb6f2b06c353_l3.png)
Zum Glück findest du hier die Nullstellen schneller als bei der ursprünglichen Funktion. Als Erstes kannst du x ausklammern.
![Rendered by QuickLaTeX.com \[ x\cdot ( 3x-6) = 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4ec428fe9c4b30ae20a8fd24018780f0_l3.png)
Wir machen uns wieder einen Trick zu Nutze: Das Produkt ist gleich 0, sobald einer der Faktoren gleich 0 ist. Deine erste potentielle Extremstelle ist also x3=0. Übrig bleibt:

Fazit: Bei den Stellen x3=0 und x4=2 könnte es sich um Extremstellen handeln.
2. Potentielle Extremstellen in zweite Ableitung einsetzen
Mit der hinreichenden Bedingung
 bzw.
bzw.  kannst du Hoch- und Tiefpunkte voneinander unterscheiden.
kannst du Hoch- und Tiefpunkte voneinander unterscheiden.

Fazit: Du hast einen Hochpunkt bei x3=0 und einen Tiefpunkt bei x4=2.
Zuletzt musst du nur noch wissen, welche y-Werte zu deinen x-Werten gehören.
3. Extremstellen in ursprüngliche Funktion einsetzen
Zuletzt setzt du x-Werte deiner Extremstellen in deine ursprüngliche Funktion ein, um die passenden y-Werte zu berechnen.

Fazit: Du hast also einen Hochpunkt bei H=(0|4) und einen Tiefpunkt bei T=(2|0)
Monotonieverhalten bestimmen
Streng monoton fallend:  / Monoton fallend:
/ Monoton fallend: 
Streng monoton steigend:  / Monoton steigend:
/ Monoton steigend: 
Bestimme die Monotonie immer nur für Intervalle bis zum nächsten Extrempunkt. Du schaust dir zuerst die Monotonie
von minus unendlich bis zum Hochpunkt bei x=0 (![Rendered by QuickLaTeX.com \left]-\infty; 0\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9aedb66cede9f4c53539d0fa2d3ec954_l3.png) ) an. Danach zwischen den Extrempunkten (
) an. Danach zwischen den Extrempunkten (![Rendered by QuickLaTeX.com \left]0; 2\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0e392df5199681e1dde35e05abed531b_l3.png) ) und zuletzt alles nach dem Tiefpunkt bei x=2 (
) und zuletzt alles nach dem Tiefpunkt bei x=2 (![Rendered by QuickLaTeX.com \left]2; +\infty\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-137fbf187f73f7843c9a910160179e24_l3.png) ). Das Monotonieverhalten kannst du gut in einer Monotonietabelle zusammenfassen:
). Das Monotonieverhalten kannst du gut in einer Monotonietabelle zusammenfassen:
| Intervall | ![Rendered by QuickLaTeX.com \left]-\infty; 0\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9aedb66cede9f4c53539d0fa2d3ec954_l3.png) |
![Rendered by QuickLaTeX.com \left]0; 2\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0e392df5199681e1dde35e05abed531b_l3.png) |
![Rendered by QuickLaTeX.com \left]2; +\infty\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-137fbf187f73f7843c9a910160179e24_l3.png) |
| Vorzeichen von f'(x) | + | – | + |
| Graph von f(x) | steigt streng monoton. | fällt streng monoton. | steigt streng monoton. |
Um das Vorzeichen der ersten Ableitung zu finden, setzt du eine beliebige Zahl aus deinem Intervall ein. Ist die Ableitung positiv, steigt deine Funktion streng monoton. Ist sie negativ, fällt sie streng monoton.
Wendepunkt und Wendetangente berechnen
Am Wendepunkt ändert der Graph seine Krümmung.
An einem Wendepunkt gilt:
![Rendered by QuickLaTeX.com \[ f''(x) = 0\quad\text{und}\quad f'''(x) \neq 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d4ec3cb099a2486db0867f6e7c4154d1_l3.png)
1. Nullstelle der zweite Ableitung finden
Wegen der notwendigen Bedingung  , ist die Wendestelle die Nullstelle der zweiten Ableitung.
, ist die Wendestelle die Nullstelle der zweiten Ableitung.

Fazit: Bei x5=1 könnte also ein Wendepunkt liegen.
2. Potentielle Wendestelle in dritte Ableitung einsetzen
Wegen der hinreichenden Bedingung  darf die dritte Ableitung am Wendepunkt nicht 0 sein.
darf die dritte Ableitung am Wendepunkt nicht 0 sein.
![Rendered by QuickLaTeX.com \[ f'''(\textcolor{red}{x_5}) = f'''(\textcolor{red}{1}) = 6 \neq 0 \Longrightarrow \text{Wendepunkt} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2206481bb1f0b63fc330b803adcd0b46_l3.png)
Fazit: Die Stelle x5=1 ist tatsächlich eine Wendestelle. Jetzt möchtest du nur noch ihren y-Wert herausfinden.
3. Wendestelle in ursprüngliche Funktion einsetzen
Zuletzt setzt du deine Wendestelle in die ursprüngliche Funktion ein, um die y-Koordinate deines Wendepunktes zu finden.
![Rendered by QuickLaTeX.com \[ f(\textcolor{red}{x_5}) = f(\textcolor{red}{1})= \textcolor{red}{1}^3 - 3\cdot \textcolor{red}{1}^2 + 4 = 1 - 3 + 4 = 2 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e04470507f5f0142735738831b8d1e37_l3.png)
Fazit: Dein Funktionsgraph hat einen Wendepunkt bei W=(1|2).
4. Finde die Wendetangente
Die Wendetangente ist eine Gerade, die am Wendepunkt die gleiche Steigung wie dein Graph hat.
Die Gleichung deiner Wendetangente
lautet: 
m ist die Steigung der Wendetangente und (xW|yW) ist der Wendepunkt.
Weil du schon weißt, wo der Wendepunkt liegt, musst du nur noch die Steigung ausrechnen. Das findest du mit der ersten Ableitung heraus. Setze deine Wendestelle (xW = x5 = 1) in die erste Ableitung ein:
![Rendered by QuickLaTeX.com \[ m = f'(\textcolor{red}{x_5}) = f'(\textcolor{red}{1}) = 3\cdot \textcolor{red}{1}^2 - 6 \cdot \textcolor{red}{1} = 3 - 6 = -3 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b9ab10d9a08de6d53aeff23233a1a689_l3.png)
Fazit: Die Wendetangente hat die Gleichung  .
.
Krümmungsverhalten bestimmen
Nachdem du den Wendepunkt kennst, kannst du auch das Krümmungsverhalten deines Graphen bestimmen.
Wenn  gilt, ist der Graph linksgekrümmt.
gilt, ist der Graph linksgekrümmt.
Wenn  gilt, ist der Graph rechtsgekrümmt.
gilt, ist der Graph rechtsgekrümmt.
Weil du weißt, dass sich die Krümmung am Wendepunkt W=(1|2) ändert, brauchst du nur das Krümmungsverhalten von zwei Punkten rechts und links vom Wendepunkt bestimmen. Nimm zum Beispiel die Stellen x=0 und x=2:

Fazit: Dein Graph ist im Intervall ![Rendered by QuickLaTeX.com \left]-\infty;1\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6020db1e353022806344d35db81e8e93_l3.png) rechtsgekrümmt und im Intervall
rechtsgekrümmt und im Intervall ![Rendered by QuickLaTeX.com \left]1;+\infty\right[](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aaca4a5652187837efd044a8135c52c7_l3.png) linksgekrümmt.
linksgekrümmt.
Wertebereich bestimmen
Als letztes musst du noch den Wertebereich ermitteln. Die Frage ist: Welche y-Werte kann deine Funktion alles ausgeben?
Ganzrationale Funktionen mit ungeradem Leitterm (z.B. x, x3, x5, …) haben immer die Menge aller reeller Zahlen als Wertemenge.
Ganzrationale Funktionen mit geradem Leitterm (z.B. x2, x4, x6, …) können nur Werte zwischen ihrem Grenzwert und ihrem Extrempunkt in ihrem Wertebereich haben.
Deine Beispielfunktion  hat einen ungeraden Leitterm (x3). Seine Wertemenge
hat einen ungeraden Leitterm (x3). Seine Wertemenge
 ist deswegen gleich der Menge aller reeller Zahlen
ist deswegen gleich der Menge aller reeller Zahlen  :
:
![Rendered by QuickLaTeX.com \[ \mathbb{W}_f = \mathbb{R} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-98d727e578d9902c975fd5e321e9766d_l3.png)
Funktionsgraph zeichnen
Jetzt hast du alle wichtigen Informationen, um den Graphen der Funktion zu zeichnen. Markiere dir alle wichtigen Punkte, bevor du deinen Graphen zeichnest:
- Einfache Nullstelle bei x = -1
- Doppelte Nullstelle bzw. Tiefpunkt bei x = 2
- Höhepunkt bzw. y-Achsenabschnitt bei (0|4)
- Wendepunkt bei (1|2)
Kurvendiskussion e-Funktion
Mit der Kurvendiskussion bei ganzrationalen Funktionen kennst du dich jetzt aus. Für deine nächste Prüfung solltest du aber auch die Exponentialfunktion untersuchen können. Sieh dir deshalb unbedingt noch unser Aufgaben-Video dazu an!

