Symmetrie Funktionen
Du fragst dich, wie du die Symmetrie bei Funktionen bestimmen kannst? Dann bist du hier genau richtig! Wenn du lieber streamst anstatt Texte zu lesen, dann klick doch einfach auf unser Video hier!
Inhaltsübersicht
Symmetrie von Funktionen einfach erklärt
Bei der Symmetrie von Funktionen unterscheidest du zwischen zwei Arten: Die Achsensymmetrie und die Punktsymmetrie.
Um das Symmetrieverhalten zu bestimmen, musst du dir immer f(-x) anschauen:
- Die Funktion ist achsensymmetrisch zur y-Achse, wenn f(-x) = f(x)
Beispiel mit f(x) = x²: f(-x) = (-x)² = x² = f(x)![\[\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-20146a6dff3301bbb3948ce996d8ecd9_l3.png "Rendered by QuickLaTeX.com")
- Die Funktion ist punktsymmetrisch zum Ursprung, wenn f(-x) = -f(x)
Beispiel mit f(x) = x³: f(-x) = (-x)³ = -x³ = -f(x)
Eine ausführlichere Erklärung und weitere Beispiele zu den Symmetrieeigenschaften siehst du jetzt.
Achsensymmetrie zur y-Achse
Eine häufige Symmetrie von Funktionen ist die Achsensymmetrie zur y-Achse. Die linke Seite der y-Achse ist ein Spiegelbild der Rechten.
Rechnerisch muss hier gelten: f(-x) = f(x). Um das für alle x zu zeigen, gehst du am besten so vor:
- f(-x) aufstellen. Du ersetzt überall x mit -x.
- Vereinfachen
- Prüfen, ob f(x) rauskommt
Klingt gar nicht so schwer, oder? Probiere das gleich mal an dieser Funktion aus:
f(x) = x4-2x2-3
Jetzt gehst du Schritt für Schritt vor:
- f(-x) aufstellen f(-x) = (-x)4-2(-x)2-3
- Vereinfachen (-x)4-2(-x)2-3 = x4-2x2-3
-
Prüfen, ob f(x) rauskommt x4-2x2-3 = f(x)
Super! Du hast gezeigt, dass die Funktion symmetrisch zur y-Achse ist. Dieses Symmetrieverhalten siehst du auch an ihrem Graphen:
Du willst lieber einen kürzeren Weg ohne viel zu rechnen? Dann ist dieser Trick für dich genau das richtige!
Ganzrationale Funktionen der Form anxn + an-1xn-1 +…+ a0 sind genau dann achsensymmetrisch zur y-Achse, wenn sie nur gerade Hochzahlen haben!
2x4+3x2+2 ist also achsensymmetrisch zur y-Achse, da x4, x2 und x0 (die 2 ist eigentlich 2x0, da x0 = 1) gerade Hochzahlen haben.
2x4+3x+1 ist nicht achsensymmetrisch zur y-Achse, da x1 (also x) eine ungerade Hochzahl hat. Ihr Symmetrieverhalten ist weder punkt- noch achsensymmetrisch.
Punktsymmetrie zum Ursprung
Eine weitere einfache Symmetrieeigenschaft ist die Punktsymmetrie zum Ursprung.
Rechnerisch muss hier für alle x gelten: f(-x) = -f(x). Um das schnell zu überprüfen, gehst du so vor:
f(-x) aufstellen. Das heißt, überall x mit -x ersetzen.
- Vereinfachen.
- Ein Minus ausklammern.
- Prüfen, ob du -f(x) hast.
Schau dir dazu direkt einmal diese Funktionsgleichung an:
f(x) = x5+2x3-x
Ist sie symmetrisch zum Ursprung?
- f(-x) aufstellen. f(-x) = (-x)5 +2(-x)3-(-x)
- Vereinfachen. (-x)5 +2(-x)3-(-x) = -x5-2x3+x
- Ein Minus ausklammern. -x5-2x3+x = – (x5+2x3-x)
-
Prüfen, ob du -f(x) hast. – (x5+2x3-x) = -f(x)
Also ist die Funktion punktsymmetrisch zum Ursprung. Das siehst du auch am Graphen:
Natürlich gibt es auch hier einen Trick, mit dem nicht mehr rechnen musst:
Ganzrationalen Funktionen der Form anxn + an-1xn-1 +…+ a0 sind genau dann punktsymmetrisch zum Ursprung, wenn sie nur ungerade Hochzahlen haben!
- 3x3+2x ist punktsymmetrisch zum Ursprung, da x3 und x1 ungerade Hochzahlen haben.
- 3x3+2x2+x ist nicht punktsymmetrisch zum Ursprung, da x2 eine gerade Hochzahl hat.
- 3x3+2 ist nicht punktsymmetrisch zum Ursprung, da die 2 = 2x0 eine gerade Hochzahl hat.
Symmetrie Funktionen Aufgaben
Aufgabe 1: Prüfe diese ganzrationale Funktion auf ihr Symmetrieverhalten:
x6+x2-16
Lösung Aufgabe 1:
Achsensymmetrie zur y-Achse prüfst du mit: f(-x) = f(x)
- f(-x) aufstellen: f(-x) = (-x)6+(-x)2-16
- Vereinfachen: (-x)6+(-x)2-16 = x6+x2-16
- Prüfen, ob es f(x) ist. Hier ist das der Fall! x6+x2-16= f(x)
Die Funktion ist also achsensymmetrisch zur y-Achse!
Tipp: Bei der Symmetrie von Funktionen dieser Form kannst du auch nur schauen, ob du ausschließlich gerade Hochzahlen hast.
Aufgabe 2: Prüfe die Symmetrie dieser Funktion. Ist sie punktsymmetrisch zum Ursprung?:
f(x) = x5+3x3+1
Lösung Aufgabe 2:
Punktsymmetrie zum Ursprung prüfst du mit: f(-x) = -f(x)
- f(-x) aufstellen: f(-x) = (-x)5+3(-x)3+1
- Vereinfachen: (-x)5+3(-x)3+1 = -x5 -3x3+1
- Ein Minus ausklammern: -x5 -3x3+1 = -(x5+3x3-1)
- Prüfen, ob es -f(x) ist. Hier ist das nicht der Fall! Denn -f(x) wäre -(x5+3x3+1)
Sie ist also nicht punktsymmetrisch zum Ursprung!
Tipp: Bei der Symmetrie von Funktionen dieser Form kannst du auch nur schauen, ob du ausschließlich ungerade Hochzahlen hast. (hier nicht der Fall, wegen der 0 bei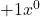 
)
Aufgabe 3: Prüfe das Symmetrieverhalten von dieser Funktion. Ist sie punktsymmetrisch zum Ursprung?
![\[f(x) = \frac{1}{x}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cb9b2d45adb96c1ec7c818437e3a01c8_l3.png "Rendered by QuickLaTeX.com")
Lösung Aufgabe 3:
Punktsymmetrie zum Ursprung prüfst du mit: f(-x) = -f(x)
-
f(-x) aufstellen:
![\[f(-x) = \frac{1}{-x}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3bae67008ba21d4a4a3c6a8942c45e16_l3.png "Rendered by QuickLaTeX.com")
-
Vereinfachen:
![\[ \frac{1}{-x} = -\frac{1}{x}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-da1277820f51eb1b1ff64be6a6424e1b_l3.png "Rendered by QuickLaTeX.com")
-
Ein Minus ausklammern:
![\[ -\frac{1}{x} = -(\frac{1}{x})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-899829695c5f1c27ec3ada03fe39e84b_l3.png "Rendered by QuickLaTeX.com")
-
Prüfen, ob es -f(x) ist. Hier ist das der Fall!
![\[-(\frac{1}{x}) = -f(x)\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-78c7e750050e18071d2a76eb7c544cef_l3.png "Rendered by QuickLaTeX.com")
Die Funktion ist also punktsymmetrisch zum Ursprung!
Aufgabe 4: Prüfe das Symmetrieverhalten von dieser Funktion. Ist sie symmetrisch zur y-Achse?
![\[f(x) = 2^{x^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5e77cb30cb59a11cc429f1761a65922e_l3.png "Rendered by QuickLaTeX.com")
Lösung Aufgabe 4:
Achsensymmetrie zur y-Achse prüfst du mit: f(-x) = f(x)
-
f(-x) aufstellen:
![\[f(-x) = 2^{(-x)^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5c91f52714d3cc83a954f6d17f0cedb9_l3.png "Rendered by QuickLaTeX.com")
-
Vereinfachen:
![\[ 2^{(-x)^2} = 2^{x^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a25702c9c4ff735940231b1fbc7efbef_l3.png "Rendered by QuickLaTeX.com")
-
Prüfen, ob es f(x) ist. Hier ist das der Fall!
![\[2^{x^2}= f(x)\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-774908e5032087af133aea9dba492cbe_l3.png "Rendered by QuickLaTeX.com")
Die Funktion ist also symmetrisch zur y-Achse!
Achsensymmetrie zu einer beliebigen Achse
Funktionen können auch zu einer beliebigen senkrechten Achse symmetrisch sein. Diese Symmetrieeigenschaft kannst du hier sehen:
Hier ist die Symmetrieachse h = 2.
Da du die links-rechts-Verschiebung berücksichtigen musst, reicht es hier nicht mehr, f(-x) = f(x) zu zeigen. Stattdessen musst du eine Vermutung über die Symmetrieachse h aufstellen und dann prüfen, ob gilt:
f(h-x) = f(h+x)
Nur wenn diese Gleichung erfüllt ist, ist h deine Symmetrieachse. Aber wie wählst du h am besten? Es gibt es 2 verschiedene Möglichkeiten:
- Die zu prüfende Symmetrieachse wird schon in der Aufgabenstellung genannt. Dann setzt du sie einfach für h ein.
- Du berechnest die Extremstellen
der Funktion und schaust dir dann den x-Wert an.
z.B.: Bei der Funktion f(x) = (x-2)2-3.
Bestimme die Nullstellen deiner Ableitung:
Du musst also für h die 2 einsetzten.
Achtung: Bis jetzt ist dein h erst eine Vermutung! Du musst das Symmetrieverhalten bei h erst noch mithilfe der Gleichung f(h-x) = f(h+x) überprüfen.
Versuche das doch gleich mal an der Funktion: f(x) = (x-2)2-3. Du gehst dabei ähnlich vor wie oben. Die Vermutung war, dass h = 2.
- Stelle f(h-x) auf: f(2-x) = ((2-x)-2)2-3
- Vereinfache: ((2-x)-2)2-3 = (-x)2-3 = x2-3
- Stelle f(h+x) auf: f(2+x) = ((2+x)-2)2-3
- Vereinfache: ((2+x)-2)2-3 = x2-3
- Prüfe, ob f(h-x) = f(h+x): f(h-x) = x2-3 = f(h+x)
Super, jetzt hast du rechnerisch nachgewiesen, dass f(x) = (x-2)2-3 achsensymmetrisch zu h = 2 ist.
Punktsymmetrie zu einem beliebigen Punkt
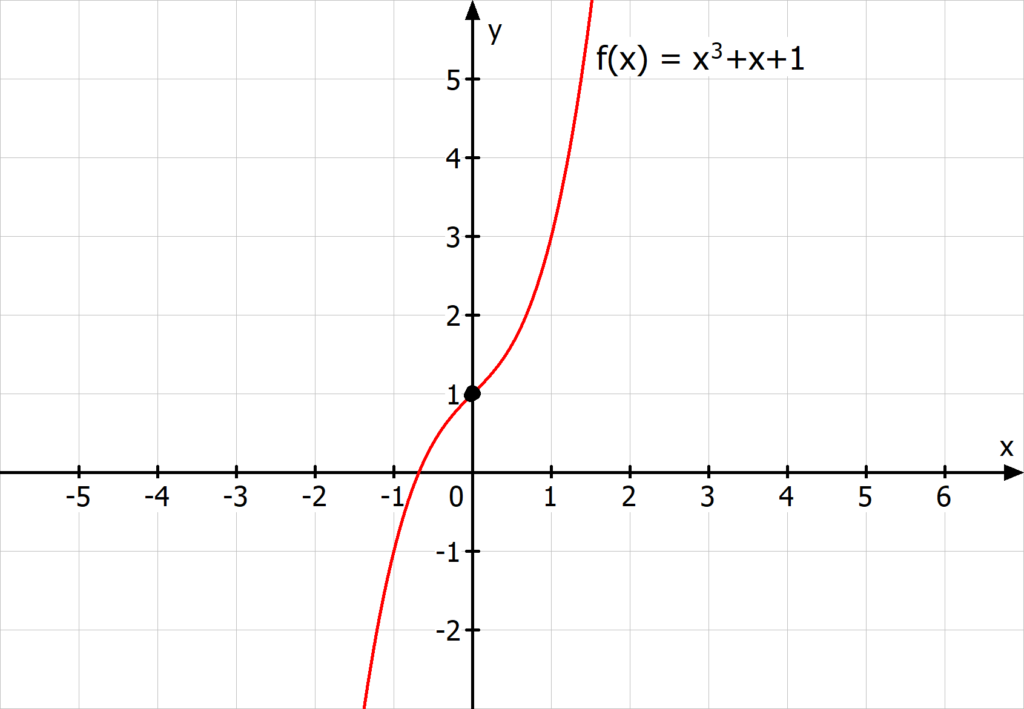
Auch bei der Punktsymmetrie kann der Graph zu einem beliebigen Punkt symmetrisch sein. Ein Beispiel für dieses Symmetrieverhalten siehst du hier:
Der Symmetriepunkt liegt bei (0|1).
Da es möglich ist, dass der Punkt vom Ursprung nach links/rechts und nach oben/unten verschoben wurde, musst du hier eine Gleichung prüfen, die beides berücksichtigt:
f(a+x)-b = -(f(a-x)-b)
Dabei ist a die x-Koordinate deines vermuteten Symmetriepunktes und b die y-Koordinate.
Doch wie wählst du diesen Punkt am besten? Dazu gibt es wieder 2 verschiedene Möglichkeiten:
- Der zu prüfende Punkt ist schon in der Aufgabenstellung gegeben.
- Du bestimmst den Wendepunkt der Funktion.
Jetzt musst du die Koordinaten deines Punktes nur noch einsetzen und die Gleichung prüfen.
Betrachte dazu die Gleichung: f(x) = x3+x+1. Wenn du den Wendepunkt bestimmst erhältst du (0|1). Überprüfe jetzt, ob es sich hier um einen Symmetriepunkt handelt.
Dein a ist hier 0, dein b ist die 1.
- Stelle f(0+x)-1 auf: f(x)-1 = x3+x+1-1
- Vereinfache: x3+x+1-1 = x3+x
- Stelle -(f(0-x)-1) auf: -(f(-x)-1) = -((-x)3+(-x)+1-1)
- Vereinfache: -((-x)3+(-x)+1-1) = -(-x3-x) = x3+x
- Prüfe, ob das gleiche rauskommt: Hier ist das der Fall! f(0+x)-1 = x3+x = -(f(0-x)-1)
Die Funktion ist also punktsymmetrisch zu P(0|1)!
Kurvendiskussion
Super, jetzt weißt du wie du die Symmetrie von Funktionen bestimmen kannst! Das Symmetrieverhalten ist Teil der Kurvendiskussion , bei der du das Aussehen eines Graphen untersuchst. Du möchtest noch mehr darüber erfahren? Dann klick doch einfach auf unser Video zu dem Thema hier!
