Kurvendiskussion
Wenn du beim Thema Kurvendiskussion noch keinen Überblick hast, bist du bei unserer Kurvendiskussions-Zusammenfassung genau richtig. Hier findest du alles, was du wissen musst. Schaue dir auch unser passendes Video dazu an!
Inhaltsübersicht
Kurvendiskussion einfach erklärt
Eine Kurvendiskussion ist die ausführliche Untersuchung einer Funktion. Dabei ermittelst du geometrische Eigenschaften des Graphen der Funktion, wie beispielsweise Nullstellen, Extrempunkte, Wendepunkte und das Verhalten im Unendlichen. Anhand dieser Eigenschaften kannst du deinen Graphen dann ganz einfach zeichnen.
In der Abbildung siehst du einige Punkte einer Funktion f(x), die du mit einer Kurvendiskussion finden kannst.
1. Definitionsbereich bestimmen (Definitionslücken)
2. Achsenabschnitte berechnen (y-Achsenabschnitt und Nullstellen)
3. Symmetrieverhalten bestimmen (Punkt- oder Achsensymmetrie)
4. Verhalten im Unendlichen (Grenzverhalten/ Limes)
5. Extrempunkte berechnen (Hochpunkte und Tiefpunkte)
6. Monotonieverhalten bestimmen (Steigungsverhalten)
7. Krümmungsverhalten bestimmen (Zweite Ableitung)
8. Wendepunkte berechnen (Links-Rechts- und Rechts-Links-Punkte)
9. Wertebereich bestimmen (Wertemenge)
Definitionsbereich bestimmen
Obwohl oft nicht extra nach ihm in Aufgaben gefragt wird, solltest du dir immer den Definitionsbereich (oder auch die Definitionsmenge) aufschreiben. Er sagt dir, welche Werte du für x in deine Funktion f(x) einsetzen darfst.
Wenn du eine dieser Rechnungen in deiner Funktion hast, musst du aufpassen!
-
 (Keine 0 unterm Bruchstrich!)
(Keine 0 unterm Bruchstrich!) -
 (Keine negativen Zahlen in Wurzeln!)
(Keine negativen Zahlen in Wurzeln!) -
 (Nur positive Zahlen in Logarithmen!)
(Nur positive Zahlen in Logarithmen!)
Falls du dir das noch mal genau angucken magst, haben wir auch ein eigenes Video zum Definitionsbereich
 .
.
Am besten verstehst du das mit einem Beispiel: Welche Zahlen darfst du in die Funktion
![Rendered by QuickLaTeX.com \[ f(x) = \frac{2x+3}{ x^2-4 } \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-09798b97303088f04fd0a930859e15f6_l3.png)
einsetzen? Deine Funktion ist ein Bruch. Unter dem Bruchstrich darf also nie eine 0 stehen. Dass bedeutet, der Term unter Bruchstrich ( ) muss immer ungleich 0 sein:
) muss immer ungleich 0 sein:

Du darfst also auch nicht den Wert -2 oder +2 für x einsetzen. Abgesehen davon darfst du jede reelle Zahl in deine Funktion einsetzen. Das alles kannst du noch in der Intervallschreibweise zusammenfassen:
![Rendered by QuickLaTeX.com \[ \mathbb{D}_f = \textcolor{blue}{\left]-\infty; +\infty\right[} \textcolor{red}{\,/ \{-2; 2\} } \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5be760992abfe1aa1bdbd0cfd8413d87_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Achsenschnittpunkte berechnen
Als Nächstes berechnest du die Schnittpunkte mit den Koordinatenachsen . Der Schnittpunkt mit der y-Achse heißt y-Achsenabschnitt und die Schnittpunkte mit der x-Achse Nullstellen.
- Nullstellen: Setze die Funktion gleich 0!
![Rendered by QuickLaTeX.com \[f(x) \overset{!}{=} 0\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9b43a037e6046c2923cdf43a69009cca_l3.png)
- y-Achsenabschnitt: Setze für x 0 in die Funktion ein!
![Rendered by QuickLaTeX.com \[f(0) = y\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5a9eca811fcef30f63f54ce7552d2ad0_l3.png)
Angenommen du hast die Funktion
![Rendered by QuickLaTeX.com \[ f(x) = 2x^2 - 16x +12 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f0424288770b98a4ca320b6ecd47bc1a_l3.png)
gegeben.
y-Achsenabschnitt
Dann berechnest du den Achsenschnittpunkt mit der y-Achse, indem du x=0 einsetzt.

x-Achsenabschnitte
Die Nullstellen berechnest du, indem du die Funktion f(x)=0 setzt und nach x umstellst. Falls du dein Wissen auffrischen magst, haben wir für dich ein Video über das Nullstellen berechnen vorbereitet. Für dieses Beispiel kannst du die Mitternachtsformel benutzen, um die Funktion umzustellen:

Symmetrieverhalten bestimmen
Funktionen können punktsymmetrisch zum Ursprung oder achsensymmetrisch zur y-Achse sein.
Achsensymmetrie zur y-Achse:
![Rendered by QuickLaTeX.com \[f(-x) = f(x)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-bcd120520c4a316f754dd15aef8520de_l3.png)
Punktsymmetrie zum Ursprung:
![Rendered by QuickLaTeX.com \[ f(-x) = -f(x) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2a8282223351dabcf5ea2f3d9f8a5db4_l3.png)
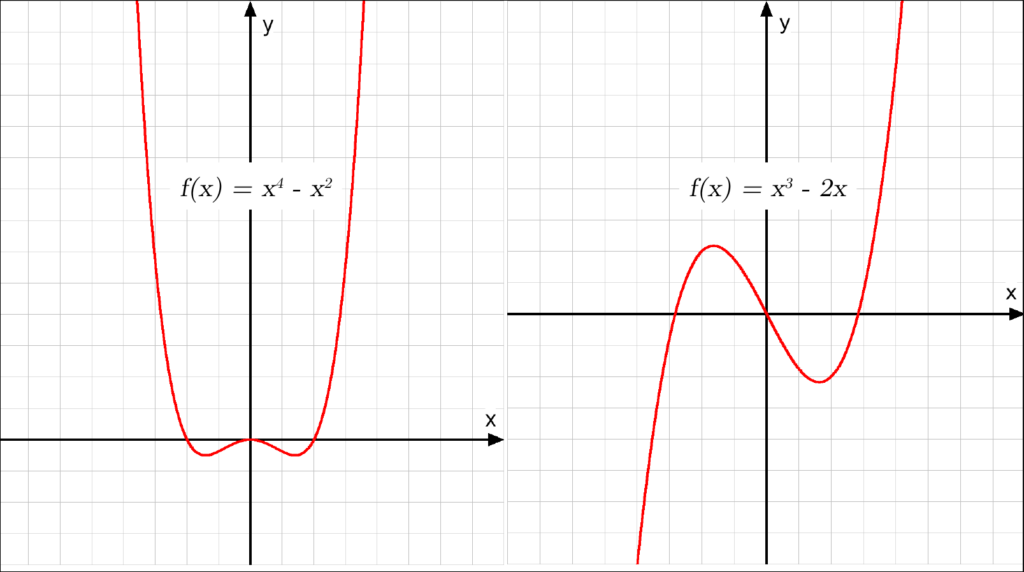
Funktionen mit geraden Exponenten (z.B.  ) sind achsensymmetrisch zur y-Achse:
) sind achsensymmetrisch zur y-Achse:

Die Funktionen mit ungeraden Exponenten (z.B.  ) sind punktsymmetrisch zum Ursprung:
) sind punktsymmetrisch zum Ursprung:

Verhalten im Unendlichen
Nach der Symmetrie schaust du dir die Grenzwerte deiner Funktion an. Du fragst dich also, was sie für sehr große und sehr kleine x-Werte macht. Dafür benutzt du den sogenannten Limes  . Angenommen du hast die Funktion
. Angenommen du hast die Funktion
![Rendered by QuickLaTeX.com \[ f(x) = 2x\cdot e^x \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-901f57efeeab2f970787c2ec7ed32153_l3.png)
Dann bestimmst du ihr Verhalten im Unendlichen
, indem du für x immer größere Werte (Verhalten gegen  ) einsetzt und überlegst, wohin die Funktion sich für immer größere Werte bewegt. Hier werden
) einsetzt und überlegst, wohin die Funktion sich für immer größere Werte bewegt. Hier werden  und
und  immer größer. Die Funktion geht gegen
immer größer. Die Funktion geht gegen  :
:
![Rendered by QuickLaTeX.com \[ \lim\limits_{x\rightarrow +\infty} 2x\cdot e^x = +\infty \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-80c48e601f362598352ad23edf8dd95c_l3.png)
Das Gleiche kannst du für immer kleinere x-Werte machen (Verhalten gegen  ). Hier geht die Teilfunktion
). Hier geht die Teilfunktion  für kleinere x-Werte gegen
für kleinere x-Werte gegen  , aber die Teilfunktion
, aber die Teilfunktion  geht nach 0. Weil
geht nach 0. Weil  schneller gegen 0 geht als
schneller gegen 0 geht als  gegen
gegen  , nähert sich die gesamte Funktion
, nähert sich die gesamte Funktion  dem Wert 0 an:
dem Wert 0 an:
![Rendered by QuickLaTeX.com \[ \lim\limits_{x\rightarrow -\infty} 2x\cdot e^x = 0 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-033b4fb93334e592e89820783553e1f2_l3.png)
Extrempunkte berechnen
Mit einer Kurvendiskussion findest du auch alle Hoch- und Tiefpunkte deiner Funktion f(x). Dabei gehst du immer so vor:
- Notwendige Bedingung: An einem Extrempunkt ist die Ableitung von f(x) gleich 0.
![Rendered by QuickLaTeX.com \[ f'(x) \overset{!}{=} 0 \;\Rightarrow\; \text{potentielle Extremstelle bei } x_E \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-075b8cc7d3cf8408822eb2e6f3eb956b_l3.png)
- Hinreichende Bedingung: Potentielle Extremstellen können Sattelpunkte oder Extrempunkte (Hoch- und Tiefpunkte) sein. Unterscheide sie mit der zweiten Ableitung!

- y-Werte der Extrempunkte: Setze die Extremstellen in die Funktion f(x) ein.
![Rendered by QuickLaTeX.com \[ f'(x_E) = 0 \;\Rightarrow\; \text{Extrempunkt bei } (x_E | f(x_E) ) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-48f8902edc1eddc8a468190e3e8c2152_l3.png)
Wenn du dir das Thema noch mal in Ruhe anschauen magst, haben wir dir auch für das Extremwerte berechnen ein Video vorbereitet.
Wiederhole das am besten mit einem Beispiel. Angenommen du hast die Funktion
![Rendered by QuickLaTeX.com \[ f(x) = \frac{1}{3} x^3 + \frac{1}{2} x^2 - 6x + 5 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4b33b5077118e2fca59ca49e73a9bf95_l3.png)
gegeben. Wo liegen ihre Hochpunkte und Tiefpunkte?
1.Schritt: Ableitung gleich 0 setzen.
![Rendered by QuickLaTeX.com \[ f'(x) = x^2 + x - 6 \overset{!}{=} 0 \;\Rightarrow\; \text{potentielle Extremstellen bei } x_1 = -3 \text{ und } x_2 = 2 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c520475693b5ebf231dae1e838ec5bc7_l3.png)
2.Schritt: Zweite Ableitung bilden und potentielle Extremstellen einsetzen.

3.Schritt: y-Werte berechnen.

Die Funktion f(x) besitzt einen Hochpunkt bei (-3|18,5) und einen Tiefpunkt bei (2|-2,3). War doch gar nicht so schwer, oder?
Monotonieverhalten bestimmen
Der nächste Schritt einer Kurvendiskussion ist die Bestimmung des Steigungsverhaltens (auch Monotonieverhalten genannt). Dabei willst du herausfinden, ob deine Funktion im Großen und Ganzen größer oder kleiner wird. Weil dir die Ableitung sagt, ob die Funktion steigt oder fällt, kannst du mit ihr die Monotonie bestimmen.

Wenn die Ableitung deiner Funktion nie gleich 0 ist, ist sie streng monoton. Die roten Graphen sind streng monoton und die blauen Kurven sind monoton.
Krümmungsverhalten bestimmen
Wenn sich die Steigung einer Funktion ändert, nennst du sie gekrümmt. Wird die Steigung größer, ist der Graph links-gekrümmt. Nimmt die Steigung ab, ist er rechts-gekrümmt.
Du kannst das Krümmungsverhalten bestimmen, indem du dir die zweite Ableitung anschaust:

Wende die Regeln gleich an einem Beispiel an! Stelle dir vor, du sollst das Krümmungsverhalten von
![Rendered by QuickLaTeX.com \[ f(x) = x^2 + 2 \;\text{und}\; g(x) = -x^2 + 1 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f1b2ea78bde598e5c5836cc9de69e045_l3.png)
bestimmen. Finde die zweite Ableitungen und du bist fertig:

Du hast es aber nicht immer so einfach wie mit diesem Beispiel. Manche Funktionen können ihr Krümmungsverhalten nämlich ändern. Mehr dazu im nächsten Abschnitt!
Wendepunkte berechnen
Das Krümmungsverhalten einer Funktion kann sich auch ändern. Das passiert an einem Wendepunkt. In dem Beispiel ist der rote Graph zuerst rechts-gekrümmt. Nach dem Wendepunkt ist er links-gekrümmt.
Die Wendepunkte findest du mit diesen 3 Schritten:
- Notwendige Bedingung: Die zweite Ableitung gleich 0 setzten.
![Rendered by QuickLaTeX.com \[ f''(x) \overset{!}{=} 0 \;\Rightarrow\; \text{potentielle Wendestellen bei } x_W \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-838a3633a368136a18e242e30e563681_l3.png)
- Hinreichende Bedingung: Die dritte Ableitung darf nicht 0 sein. Außerdem gibt es Links-Rechts- und Rechts-Links-Wendepunkte. Unterscheide sie mit der dritten Ableitung!

- y-Werte berechnen: Setzte die Wendestelle in die Funktion ein.
![Rendered by QuickLaTeX.com \[ f''(x_W) = 0 \;\Rightarrow\; \text{Wendepunkt bei } (x_W|f(x_W))\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-440bed0b010b20c897e2482cb06c5429_l3.png)
Probiere die Regeln gleich an einem Beispiel aus! Angenommen du hast die Funktion
![Rendered by QuickLaTeX.com \[f(x) = \frac{1}{6} x^3 -x^2 + \frac{5}{2} x - \frac{8}{6} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c2e62dc30f701ff7766fde2409624a83_l3.png)
gegeben. Wo liegt ihr Wendepunkt? Wie ändert sich dort die Krümmung?
1.Schritt: Zweite Ableitung gleich 0 setzen.
![Rendered by QuickLaTeX.com \[ f''(x) = x - 2 \overset{!}{=} 0 \;\Rightarrow\; \text{potentielle Wendestelle bei } x_W = 2 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8b9da897b650869bd0ac71756a158aa3_l3.png)
2.Schritt: Dritte Ableitung bilden und Vorzeichenwechselkriterium beachten!
![Rendered by QuickLaTeX.com \[ f'''(x) = 1 > 0 \;\Rightarrow\; \text{Rechts-Links-Wendepunkt}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a706ad57aec7f8be05c1392d2968dd89_l3.png)
3.Schritt: y-Wert berechnen.
![Rendered by QuickLaTeX.com \[ y_W = f(x_W) = f(2) = 1 \;\Rightarrow\; \text{Wendepunkt bei } (2|1) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-90161548dfd9a151b9532a1ce9da4da5_l3.png)
Die Funktion f(x) hat also einen Wendepunkt bei (2|1). Der Graph wechselt dort von rechts- zu links-gekrümmt. War doch gar nicht so schwer, oder?
Wertebereich bestimmen
Der Wertebereich W sind alle y-Werte, die du ausrechnen kannst, wenn du alle erlaubten x-Werte in deine Funktion f(x) einsetzt. Die Wertemenge enthält also alle y-Werte, welche dir deine Funktion geben kann.
Die Funktion
![Rendered by QuickLaTeX.com \[f(x) = x^2 + 2 \;\Rightarrow\; \mathbb{W} = [2;\infty[ \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-520e3cc04289ba5bad9344abcec3d0c4_l3.png)
kann zum Beispiel keine Werte kleiner als 2 haben. Gleichzeitig hat sie aber keine Begrenzung nach oben. Mit f(x) kannst du also y-Werte zwischen 2 und Unendlich ausrechnen.
Kurvendiskussion — häufigste Fragen
(ausklappen)
Kurvendiskussion — häufigste Fragen
(ausklappen)-
Wie erkenne ich schnell, ob eine Funktion Polstellen hat?Polstellen erkennst du schnell, indem du prüfst, ob der Nenner irgendwo 0 wird. Bei gebrochenrationalen Funktionen löst du Nenner
 und schaust, ob der Zähler dort nicht auch 0 ist. Beispiel: Bei
und schaust, ob der Zähler dort nicht auch 0 ist. Beispiel: Bei  sind
sind  Polstellen, weil
Polstellen, weil  .
.
-
Welche Fehler passieren oft beim Nullstellen finden bei Brüchen?Ein häufiger Fehler ist, den Nenner gleich 0 zu setzen, obwohl Nullstellen nur aus dem Zähler kommen. Bei
 gilt: Nullstellen löst du mit
gilt: Nullstellen löst du mit  , aber nur für Stellen mit
, aber nur für Stellen mit  . Beispiel:
. Beispiel:  hat keine Nullstelle, weil
hat keine Nullstelle, weil  gar nicht im Definitionsbereich liegt.
gar nicht im Definitionsbereich liegt.
-
Wie prüfe ich Extrempunkte, wenn die zweite Ableitung null ist?Wenn
 ist, reicht der Test mit der zweiten Ableitung nicht, dann prüfst du weiter mit höheren Ableitungen oder dem Vorzeichenwechsel von
ist, reicht der Test mit der zweiten Ableitung nicht, dann prüfst du weiter mit höheren Ableitungen oder dem Vorzeichenwechsel von  . Wechselt
. Wechselt  von plus nach minus, liegt ein Hochpunkt vor, von minus nach plus ein Tiefpunkt. Bleibt das Vorzeichen gleich, ist es kein Extrempunkt.
von plus nach minus, liegt ein Hochpunkt vor, von minus nach plus ein Tiefpunkt. Bleibt das Vorzeichen gleich, ist es kein Extrempunkt.
-
Wie erkenne ich einen Wendepunkt ohne dritte Ableitung?Einen Wendepunkt erkennst du ohne dritte Ableitung daran, dass
 an der Stelle das Vorzeichen wechselt. Dazu bestimmst du Kandidaten mit
an der Stelle das Vorzeichen wechselt. Dazu bestimmst du Kandidaten mit  und testest links und rechts davon das Vorzeichen von
und testest links und rechts davon das Vorzeichen von  . Beispiel: Wenn
. Beispiel: Wenn  und
und  , dann liegt zwischen 1 und 3 ein Wechsel, also eine Wendestelle.
, dann liegt zwischen 1 und 3 ein Wechsel, also eine Wendestelle.
-
Wie bestimme ich den Wertebereich bei Funktionen mit Definitionslücken?Den Wertebereich bei Definitionslücken bestimmst du, indem du die Funktion auf jedem Definitionsintervall getrennt untersuchst. Dafür nutzt du Extrempunkte, Randverhalten an den Lücken (z.B. gegen
 ) und das Verhalten im Unendlichen. Beispiel: Bei
) und das Verhalten im Unendlichen. Beispiel: Bei  ist
ist  ausgeschlossen und der Wertebereich ist
ausgeschlossen und der Wertebereich ist  , also
, also  .
.
Ableiten bestimmter Funktionen
Häufig musst du auch Funktionen diskutieren, die eine e-Funktion, Logarithmus, Wurzeln oder trigonometrische Funktionen besitzen. Dann ist es nicht immer leicht die Ableitungen von den Funktionen
zu finden. Um die Kurvendiskussion auch bei diesen Funktionen leicht durchführen zu können, musst du dir unbedingt unser Video dazu anschauen.