Ableitungsregeln einfach erklärt

Welche Ableitungsregeln gibt es?

Hier hast du eine Übersicht über alle Ableitungsregeln, die du brauchst:

Ableitungsregeln Übersicht

Ableitungsregel	Funktion	Ableitung
Konstantenregel
Potenzregel
Faktorregel
Summenregel
Differenzregel
Produktregel
Quotientenregel
Kettenregel

Schau dir direkt die einzelnen Regeln noch einmal genauer an.

Ableitung einer Konstante

Wenn du eine konstante Funktion ableitest, ist deine Ableitung immer Null. 

Schau dir dazu gleich ein Beispiel an:

f(x) = 1

Die Ableitung von f ist 0:

f'(x) = 0

Aber wie sieht die Ableitung von x aus?

Ableitung von x

Wenn du x ableiten willst, ist die Ableitung immer die Zahl, die vor dem x steht:

Beispiel 1:

f(x) = 1 · x

Bei der Ableitung x bleibt also nur die Zahl stehen, die vor dem x steht. Also ist x abgeleitet gleich 1:

f'(x) = 1

Beispiel 2: 

f(x) = 5 · x + 3

Hier bleibt bei der Ableitung wieder die Zahl vor dem x stehen:

f'(x) = 5 + 0

Wichtig ist aber, dass du auch Potenzen ableiten kannst.

Ableitungsregel Potenz

Die Ableitungsformel bei Potenzen lautet:

Beispiel 1:

f(x) = x³

Du musst nur die 3 vor das x schreiben und im Exponenten von der 3 eine 1 abziehen:

f'(x) = 3 · x^3-1 = 3 · x²

Beispiel 2:

f(x) = x⁵

Bei der Ableitung von f schreibst du die 5 vor das x und im Exponenten ziehst du eine 1 ab:

f'(x) = 5 · x^5-1 = 5 · x⁴

Wenn aber vor der Potenz noch eine Zahl steht, brauchst du die Faktorregel.

Ableitungsregel Faktor

Wenn deine Funktion ein Vielfaches einer anderen Funktion ist, kannst du mit der Faktorregel einfach die andere Funktion ableiten und den Faktor vorne stehen lassen:

Beispiel 1:

f(x) = 3 · x³

Dafür musst du nur die Potenz ableiten und die 3 bleibt vorne stehen:

f'(x) = 3 · 3 · x² = 9 · x²

Beispiel 2:

f(x) = 7 · x⁴

Wieder leitest du die Potenz ab und die 7 lässt du vorne stehen:

f'(x) = 7 · 4 · x³ = 28 · x³

Ableitungsregel Summe (Summenregel)

Möchtest du eine Summe ableiten , musst du nur von den einzelnen Summanden die Ableitung bilden:

Beispiel 1:

f(x) = 5x + x²

Du musst nur die einzelnen Summanden ableiten:

f'(x) = 5 + 2x

Beispiel 2:

f(x) = 4x³ + 3x²

Für die Ableitung musst du einfach die beiden Summanden ableiten und wieder eine neue Summe bilden:

f(x) = 12x² + 6x

Wenn du eine Differenz ableitest, funktioniert das fast genau so.

Ableitungsregel Differenz (Differenzregel)

Möchtest du eine Differenz ableiten , brauchst du nur die einzelnen Teile ableiten:

Beispiel:

f(x) = 5x – x²

Du musst nur 5x und x² einzeln ableiten:

f'(x) = 5 – 2x

Du siehst also, dass das genauso wie bei der Summe funktioniert.

Wenn du wiederum ein Produkt aus zwei Funktionen ableiten möchtest, brauchst du die Produktregel.

Ableitungsregel Multiplikation (Produktregel)

Wenn du wiederum ein Produkt aus zwei Funktionen ableiten möchtest, brauchst du die Produktregel .

Schau dir dazu gleich mal ein Beispiel an: 

f(x) = (x² + x) · (2x)

• Jetzt musst du zuerst g(x) und h(x) herausschreiben:

g(x) = x² + x

h(x) = 2x

• Dann leitest du die beiden Funktionen ab:

g'(x) = 2x + 1

h'(x) = 2

• Jetzt brauchst du nur noch alles in die Ableitungsformel einsetzen:

f'(x) = g'(x) · h(x) + g(x) · h'(x) = (2x + 1) · (2x) + (x² + x) · (2)

Ableitung Division (Quotientenregel)

Wenn du einen Bruch mit zwei Funktionen ableiten willst, hilft dir die Ableitungsregel:

Hier hast du ein Beispiel:

• Jetzt musst du zuerst g(x) und h(x) rausschreiben:

• Dann musst du die beiden Funktionen ableiten:

• Jetzt brauchst du nur noch alles in die Ableitungsformel einzusetzen:

Kettenregel

Wenn du eine verkettete Funktion ableiten willst, kannst du dir folgende Ableitungregel merken:

Die Funktion h findest du auch unter der Bezeichnung innere Funktion. Dagegen heißt g äußere Funktion.

Merke: „Äußere Ableitung mal innere Ableitung.“

Ein Beispiel für eine verkettete Funktion wäre:

f(x)=(7x² + 3 )³

In diesem Fall lautet die

• innere Funktion h(x) und ihre Ableitung h'(x): 

h(x)= 7x² + 3 ⇒ h'(x)= 14x

• äußere Funktion g(x) und ihre Ableitung g'(x):

g(x)= x³ ⇒ g'(x)= 3x²

Für f'(x) setzt du nun die Ableitungen h'(x) und g'(x) zusammen mit h(x) in die Formel der Kettenregel ein: 

f'(x) = g'(h(x)) · h'(x) = 3 · (7x² + 3)² · 14x                  

Noch mehr Beispiele findest du in unserem extra Beitrag . 

Es gibt aber einige Funktionen, die eine ganz besondere Ableitung haben.

Spezielle Ableitungen

Die wichtigsten Ableitungen haben wir hier für dich zusammengefasst:  

	Funktion	Ableitung
Wurzel ableiten
Ableitung Cosinus
Ableitung Sinus
Ableitung Tangens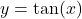
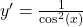e Funktion ableiten
ln ableiten

Eine Ableitungsregel, die du manchmal auch brauchst, ist die Ableitung von a^x. Hierfür lautet die Ableitung dann immer ln(a) · a^x.

Am Besten übst du jetzt aber nochmal die einzelnen Mathe Ableitungsregeln an ein paar Aufgaben.

Ableitungsregeln Aufgaben

Jetzt zeigen wir dir zwei Aufgaben zu den Ableitungsregeln. Die erste Aufgabe beinhaltet ein Produkt von Funktionen, während die zweite einen Quotienten von Funktionen behandelt.

Ableitungsregeln Aufgabe 1: Produkt von Funktionen

Die folgende Funktion soll abgeleitet werden:

(a) Welche „Form“ von Funktion hast du vorliegen und welche Ableitungsregel musst du verwenden? Notiere die Ableitungsregel.

(b) Identifiziere die einzelnen Bestandteile der festgelegten „Form“.

(c) Nutze die Ableitungsregeln, um die einzelnen Bestandteile abzuleiten.

(d) Baue die gesuchte Ableitung zusammen durch Anwendung der Ableitungsregeln.

Lösung Aufgabe 1

(a) Die Funktion ist als Produkt zweier Funktionen zusammengebaut. Daher muss die Produktregel verwendet werden. Diese lautet:

(b) Die Funktion ist das Produkt der Funktionen:

(c) Die Funktion ist die Verkettung der Funktionen und .

Gemäß der Kettenregel erhalten wir:

Die Funktion ist die Verkettung der Funktionen und .

Erneut erhalten wir nach der Kettenregel:

(d) Wir haben nun alle Bestandteile zusammen. Unter Verwendung der Produktregel bekommen wir:

Ableitungsregeln Aufgabe 2: Quotient von Funktionen

Die folgende Funktion soll abgeleitet werden:

(a) Welche „Form“ von Funktion hast du vorliegen und welche Ableitungsregel musst du verwenden? Notiere die Ableitungsregel.

(b) Identifiziere die einzelnen Bestandteile der festgelegten „Form“.

(c) Nutze die Ableitungsregeln, um die einzelnen Bestandteile abzuleiten.

(d) Baue die gesuchte Ableitung zusammen durch Anwendung der Ableitungsregeln.

Lösung Aufgabe 2

(a) Die Funktion ist als Quotient zweier Funktionen zusammengebaut. Daher muss die Quotientenregel verwendet werden. Diese lautet:

(b) Die Funktion ist der Quotient aus den Funktionen:

(c) Die Funktion ist die Verkettung aus den Funktionen:

Nach der Kettenregel erhalten wir:

Die Funktion ist die Summe aus den Funktionen:

Der letzte Summand kann unter Verwendung der Faktorregel abgeleitet werden. Wir erhalten insgesamt:

(d) Wir haben nun alle Bestandteile zusammen. Unter Verwendung der Quotientenregel bekommen wir:

.

Ableitung bestimmter Funktionen

Du siehst, dass du für manche Funktionen wie beim Sinus oder der e-Funktion eine spezielle Ableitungsregel brauchst. Schau dir dafür am besten gleich unser Video zu Ableitung bestimmter Funktionen an.