Diskriminante
In diesem Beitrag beschäftigen wir uns mit der Diskriminante. Wir zeigen dir die Formeln für die Diskriminante und was sie mit quadratischen Gleichungen zu tun hat.
Du möchtest das Thema anschaulich erklärt bekommen? Wunderbar! Dann schaue dir unser Video zu diesem Thema an.
Inhaltsübersicht
Diskriminante einfach erklärt
Die Diskriminante D ist der Ausdruck unter der Wurzel der Mitternachtsformel (auch abc-Formel )

beziehungsweise der pq-Formel

Die Diskriminante sagt dir, wie viele Lösungen eine quadratische Gleichung besitzt. Dabei gilt:
- D>0: zwei Lösungen,
- D=0: eine Lösung,
- D<0: keine Lösung.
Was ist eine Diskriminante?
Betrachten wir eine quadratische Gleichung der Form
 ,
,
wobei  ,
,  und
und  reelle Zahlen sind. Du suchst nach den Werten von
reelle Zahlen sind. Du suchst nach den Werten von  für welche die quadratische Funktion
für welche die quadratische Funktion
 den Wert Null annimmt; du berechnest also die Nullstellen
dieser Funktion. Zum Lösen kannst du die Mitternachtsformel
(auch abc-Formel
) verwenden
den Wert Null annimmt; du berechnest also die Nullstellen
dieser Funktion. Zum Lösen kannst du die Mitternachtsformel
(auch abc-Formel
) verwenden
 .
.
Nun kann die quadratische Gleichung auch in folgender Form vorliegen
 ,
,
das heißt vor dem Ausdruck 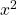 steht nur eine 1. Hier kannst du auch die pq-Formel
verwenden
steht nur eine 1. Hier kannst du auch die pq-Formel
verwenden
 .
.
Möchtest du mehr dazu erfahren, insbesondere vorgerechnete Beispiele sehen, dann klicke einfach auf die Verlinkungen zu unseren extra Beiträgen.
Beide Formeln besitzen einen Wurzelausdruck. Und genau der Ausdruck unter der Wurzel wird Diskriminante genannt.
Für die Mitternachtsformel ist die Diskriminante
 .
.
Für die pq-Formel lautet die Diskriminante
 .
.
Wenn du eine quadratische Gleichung gegeben hast, kannst du in der Regel durch bloßes Hinschauen nicht erkennen, ob diese Gleichung überhaupt Lösungen besitzt. An dieser Stelle kommt dir die Diskriminante zur Hilfe. Mit ihr kannst du ohne viel Aufwand bestimmen, ob sie Lösungen besitzt. Sie teilt dir auch mit, wie viele Lösungen es gibt. Dabei gilt folgende Merkregel.
Bezeichnen wir die Diskriminante mit  , dann gilt
, dann gilt
 ,
,


 .
.
Hinweis: Für den Fall  müsstet du die Wurzel über einer negativen Zahl ziehen. Dieser Prozess benötigt aber die Erweiterung der reellen Zahlen
müsstet du die Wurzel über einer negativen Zahl ziehen. Dieser Prozess benötigt aber die Erweiterung der reellen Zahlen  zu den komplexen Zahlen
zu den komplexen Zahlen  , was man dann erst im Studium lernt.
, was man dann erst im Studium lernt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Vorgehen
Angenommen wir haben eine beliebige quadratische Gleichung gegeben
 .
.
Schritt 1: Du untersuchst, ob der Faktor vor dem 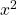 eins ist oder nicht. Abhängig davon wählst du den entsprechenden Ausdruck für die Diskriminante.
eins ist oder nicht. Abhängig davon wählst du den entsprechenden Ausdruck für die Diskriminante.
Schritt 2: Nun identifizierst du alle Komponenten, die du zum Berechnen der Diskriminante benötigst. Bei der Mitternachtsformel sind das die Paramater  ,
,  und
und  , bei der pq-Formel die Parameter
, bei der pq-Formel die Parameter  und
und  .
.
Schritt 3: Jetzt nimmst du alle Komponenten, setzt sie in die Formel für  ein und rechnest das Ergebnis aus.
ein und rechnest das Ergebnis aus.
Schritt 4: Falls gefragt, kannst du nun bestimmen, wie viele Lösungen es gibt.
Beispiel
Als Beispiel betrachten wir die folgende Gleichung
 .
.
Schritt 1: Der Faktor vor dem 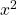 ist vier. Demnach verwenden wir die Diskriminante der Mitternachtsformel
ist vier. Demnach verwenden wir die Diskriminante der Mitternachtsformel
 .
.
Schritt 2: Wir benötigen die Komponenten  ,
,  und
und  . Diese sind
. Diese sind
 und
und  .
.
Schritt 3: Nun nehmen wir alle gefundenen Komponenten und setzen sie in D ein. Damit erhalten wir
 .
.
Schritt 4: Da  gilt, hat
gilt, hat  zwei Lösungen.
zwei Lösungen.
Diskriminante Anwendung: Schnittstelle(n) zweier Funktionen
Nehmen wir an, dass wir zwei Funktionen  und
und  gegeben haben. Wir wollen die Werte für
gegeben haben. Wir wollen die Werte für  finden, wo sich beide Funktionen schneiden; wir suchen also nach den Schnittstellen. Damit sich die Funktionen überhaupt an einer Stelle
finden, wo sich beide Funktionen schneiden; wir suchen also nach den Schnittstellen. Damit sich die Funktionen überhaupt an einer Stelle  schneiden, müssen die Funktionswerte gleich sein, das heißt
schneiden, müssen die Funktionswerte gleich sein, das heißt
 .
.
Wir können das folgendermaßen umformen.

Damit haben wir das Suchen der Schnittstellen der Funktionen  und
und  auf das Berechnen von Nullstellen der Funktion
auf das Berechnen von Nullstellen der Funktion 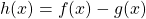 reduziert. Im speziellen Fall, dass die Differenz der beiden Funktionen eine quadratische Funktion ist, also
reduziert. Im speziellen Fall, dass die Differenz der beiden Funktionen eine quadratische Funktion ist, also
 ,
,
können wir mit der Diskriminante bestimmen, ob  Nullstellen besitzt. Damit stellen wir gleichzeitig fest, ob die Funktionen
Nullstellen besitzt. Damit stellen wir gleichzeitig fest, ob die Funktionen  und
und  Schnittstellen besitzen.
Schnittstellen besitzen.
Diskriminante Aufgaben
In diesem Abschnitt rechnen wir gemeinsam zwei Aufgaben aus.
Aufgabe 1: Diskriminante berechnen
Gegeben ist die folgende Gleichung
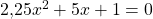 .
.
(a) Besitzt diese quadratische Gleichung Lösungen und falls Ja, wie viele?
(b) Berechne gegebenenfalls die Lösung(en).
Lösung: Aufgabe 1
(a) Der Faktor vor dem Ausdruck 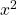 ist nicht gleich 1. Daher verwenden wir die Diskriminante der Mitternachtsformel. Wir erhalten
ist nicht gleich 1. Daher verwenden wir die Diskriminante der Mitternachtsformel. Wir erhalten
 .
.
Damit ist  und somit gibt es zwei Lösungen.
und somit gibt es zwei Lösungen.
(b) Zum Berechnen der Lösungen verwenden wir die Mitternachtsformel. Wir bekommen

und damit gilt
 und
und
 .
.
Aufgabe 2: Diskriminante berechnen
Gegeben ist die folgende Gleichung
 .
.
(a) Besitzt diese quadratische Gleichung Lösungen und falls Ja, wie viele?
(b) Berechne gegebenenfalls die Lösung(en).
Lösung: Aufgabe 2
(a) Der Faktor vor dem Ausdruck 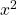 ist gleich 1. Daher verwenden wir die Diskriminante der pq-Formel. Wir erhalten
ist gleich 1. Daher verwenden wir die Diskriminante der pq-Formel. Wir erhalten
 .
.
Damit ist  und es gibt zwei Lösungen.
und es gibt zwei Lösungen.
(b) Zum Berechnen der Lösungen verwenden wir die pq-Formel. Wir bekommen

und damit gilt
 und
und
 .
.
