Betrag komplexe Zahl

Betrag einer komplexen Zahl einfach erklärt

Der Betrag einer komplexen Zahl z ist ihr Abstand zum Ursprung. Du schreibst ihn mithilfe von Betragsstrichen auf: |z|

Hast du die komplexe Zahl z = x + i • y gegeben, dann berechnest du ihren Betrag mit:

➡️ Beispiel:

z = 5 + i • 4

Eigenschaften des Betrags komplexer Zahlen

Der Betrag komplexer Zahlen hat einige wichtige Eigenschaften, die dir bei Berechnungen helfen können.

• Nichtnegativität: |z| ≥ 0 für alle z ∈ ℂ
  Der Betrag einer komplexen Zahl ist immer null oder größer, weil er den Abstand von $z$ zum Ursprung beschreibt — und ein Abstand kann nie negativ sein.
   
• Betrag von 0: |z| = 0  ⟺  z = 0
  Der Betrag einer komplexen Zahl ist genau dann null, wenn die Zahl selbst null ist.
   
• Multiplikativität: |z₁ ⋅ z₂ | = |z₁| ⋅ |z₂| für alle z₁, z₂ ∈ ℂ 
  Wenn du zwei komplexe Zahlen miteinander multiplizierst, ist der Betrag des Ergebnisses gleich dem Produkt der beiden Beträge.
  Du kannst also beide Zahlen multiplizieren und dann den Betrag berechnen, oder erst die Beträge der einzelnen Zahlen berechnen und sie dann miteinander multiplizieren. Das Ergebnis ist das gleiche.
   
• Division:
  Wenn du den Betrag eines Bruchs aus zwei komplexen Zahlen berechnen willst, gibt es zwei Möglichkeiten. Entweder teilst du den Betrag der ersten Zahl durch den Betrag der zweiten oder du führst zuerst die Division aus und berechnest dann den Betrag des Ergebnisses.
   
  Wichtig: Die Division geht nur, wenn z₂ nicht 0 ist.
   
• Dreiecksungleichung: |z₁ + z₂| ≤ |z₁| + |z₂| für alle z₁, z₂ ∈ ℂ 
  Wenn du zwei komplexe Zahlen addierst, ist der Betrag der Summe nie größer als die Summe der Beträge der beiden Zahlen.

Betrag einer komplexen Zahl in kartesischen Koordinaten

In kartesischen Koordinaten stellst du z mithilfe ihrer x-Koordinate und y-Koordinate dar: z = x + i ⋅ y.

➡️ Beispiel:

Für z = 2 + i ⋅ 7 liegt der repräsentative Punkt in der Ebene bei (2,7).

Der Betrag von z beschreibt den Abstand dieses Punktes zum Ursprung (0,0). Diesen Abstand berechnest du mit der Formel :

direkt ins Video springen

Die verwendete Formel entspricht dem Satz des Pythagoras. Du bildest hierbei mit den Längen x und y sowie dem Punkt (x,y) ein rechtwinkliges Dreieck. Dessen Hypotenuse ist der Abstand zum Koordinatenursprung.

Wenn du dir also komplexe Zahlen wie z, w oder u als Punkte in einer Ebene vorstellst, dann entspricht deren Betrag geometrisch der Länge der Verbindungslinie vom Ursprung (0,0) zum entsprechenden Punkt (x,y).

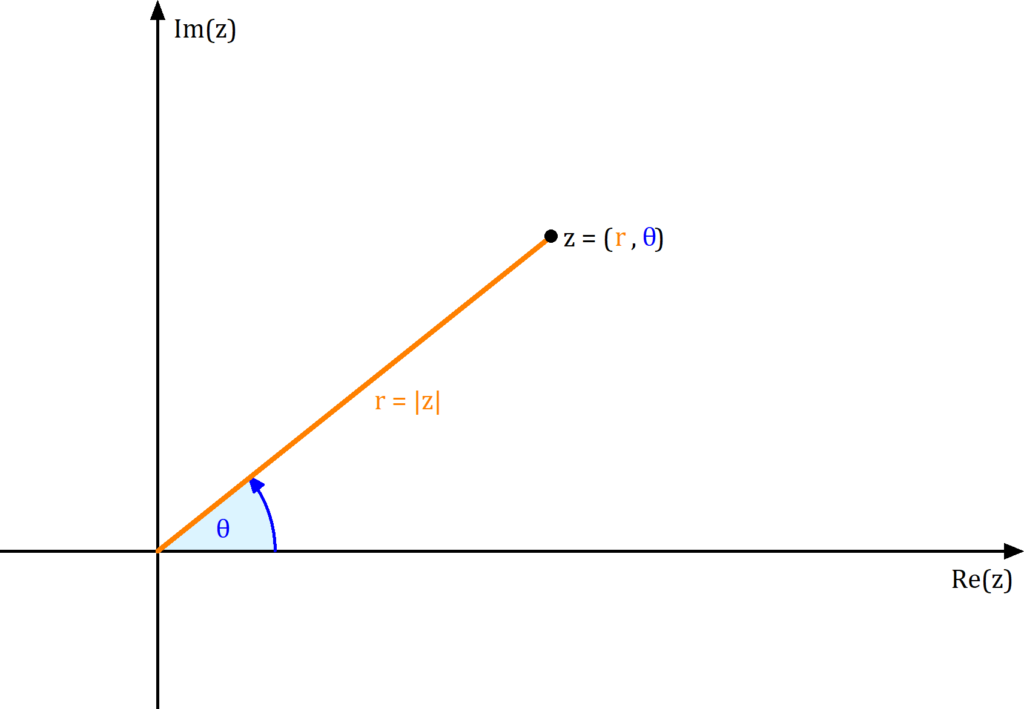
Betrag einer komplexen Zahl in Polarkoordinaten

Du kannst z auch in Polarkoordinaten darstellen. Hierzu verwendest du den Abstand r vom Ursprung und den Winkel θ.

direkt ins Video springen

Du kannst z dann folgendermaßen schreiben:

z = r • e^{i • θ}

Der Buchstabe e steht hier für die e-Funktion. Den Betrag von z kannst du direkt ablesen:

|z| = r

Das r ist der Abstand vom Ursprung und genau das ist schließlich die Bedeutung von |z|.

➡️ Beispiel:

z = 2 • e^{i • ½π}

Der Betrag ist einfach ablesbar:

|z| = 2

Komplexe Zahlen

Natürlich kannst du auch über den Betrag hinaus mit komplexen Zahlen rechnen. In unserem Video erklären wir dir, wie das geht.