Video

Quiz

Hier geht's zum Video „Lineare Funktionen“

Hier geht's zum Video „Wurzel ableiten“

Hier geht's zum Video „pq Formel“

Hier geht's zum Video „Satz von Vieta“

Hier geht's zum Video „abc Formel“

Hier geht's zum Video „Mitternachtsformel“

Hier geht's zum Video „Quadratische Ergänzung“

Quadratische Gleichungen

Wichtige Inhalte in diesem Video

Quadratische Gleichungen einfach erklärt

Arten quadratischer Gleichungen

Quadratische Gleichungen lösen: ax2+bx+c=0

In diesem Artikel erklären wir unterschiedliche quadratische Gleichungen und zeigen dir anhand von vielen Beispielen, mit welchen Formeln du sie am schnellsten lösen kannst. Am Ende des Artikels findest du einige Aufgaben zum selber Üben.

Wenn du lieber in einer direkten Schritt für Schritt Anleitung verstehen willst, wie du quadratische Gleichungen lösen kannst, dann schau dir unser Video an.

Inhaltsübersicht

Quadratische Gleichungen einfach erklärt

im Videozur Stelle im Video springen

Was quadratische Gleichungen sind, lässt sich ganz einfach erklären: Es sind Gleichungen, die immer mindestens ein x²enthalten, aber keine höheren Potenzen wie beispielsweise x³oder x⁴ . Wichtig ist dabei, dass du jede quadratische Gleichung auf eine ganz bestimmte allgemeine Form bringen kannst.

Quadratische Gleichungen: Darstellungsweisen

Allgemeine Form: ax²+bx+c=0

Normalform: x²+px+q=0

Die Parameter a, b, c, p und q stehen dabei für beliebige reelle Zahlen, du darfst alles einsetzen außer a=0. Die Normalform ist dabei der Spezialfall der allgemeinen Form mit a=1.

Wenn du quadratische Gleichungen lösen willst, gibt es entweder eine, zwei oder keine Lösung.

Übrigens: Um die Nullstellen einer quadratischen Funktion zu berechnen, musst du immer eine quadratische Gleichung lösen !

Parabel, Parabeln, Nullstellen Parabel, quadratische Funktionen, quadratische Funktion — Quadratische Gleichungen lösen zur Nullstellen-Berechnung

Arten quadratischer Gleichungen

im Videozur Stelle im Video springen

Quadratische Gleichungen unterscheiden sich, je nachdem, welche Zahlen für a, b oder c eingesetzt werden. Die verschiedenen Arten stellen wir dir in diesem Abschnitt genauer vor.

Reinquadratische Gleichungen

Reinquadratische Gleichungen enthalten außer dem quadratischen Term x² kein weiteres x, da in diesem Fall stets b=0 ist. Quadratische Gleichungen dieser Art kannst du daher mittels Äquivalenzumformungen stets auf die folgende Form bringen:

Reinquadratische Gleichung

ax²+c=0

Wichtig ist auch hier, dass in jedem Fall $a \ne 0$ ist. Typische Beispiele für solche quadratische Gleichungen sind

2x²-4=0
x²=0

Gemischt quadratische Gleichungen

Im Gegensatz dazu enthalten gemischte quadratischen Gleichungen neben dem quadratischen Ausdruck x² immer ein lineares Glied bx. In manchen dieser Fälle ist c=0, dann erhältst du eine quadratische Gleichung der Form

ax²+bx=0.

Für $c \not = 0$ liegt die quadratische Gleichung in allgemeiner Form vor

Quadratische Gleichung in allgemeiner Form

ax²+bx+c=0.

Zwei typische Beispiele dafür sind

-x²+5x+1=0
3x²+x-2=0

Merke: Mittels Äquivalenzumformungen kannst du jede quadratische Gleichung auf die allgemeine Form beziehungsweise auf die Normalform bringen. Um ausgehend von der allgemeinen Form die Normalform zu bestimmen, musst du lediglich durch den Faktor a teilen. In diesem Fall ist $p=\frac{b}{a}$ und $q=\frac{c}{a}$ .

ax²+bx+c=0 $\bigg| \div a$

Quadratische Gleichung in Normalform

x²+px+q=0

Beispiele und Nicht-Beispiele

Weitere Beispiele für quadratische Gleichungen lauten:

x²=x+1=0
x(x-3)=6
2x²+8=0
(x-2)(x+5)=0

Keine quadratischen Gleichungen liegen beispielsweise hier vor:

2x+3=0
(x²+4x)(x+3)=0
x³-x=5
$\sqrt{x}+3=9$

Quadratische Gleichungen lösen ist abhängig von ihrer Art unterschiedlich schwer. Im nächsten Abschnitt zeigen wir dir explizit am Beispiel, wie du bei den verschiedenen Fällen am besten vorgehst.

Quadratische Gleichungen lösen: ax²+c=0

Am einfachsten kannst du reinquadratische Gleichungen der Form ax²+c=0 lösen, indem du die Gleichung nach x²auflöst und dann die Wurzel ziehst.

ax²+c=0 $\bigg| -c, \quad \div a$

$x^2 = -\frac{c}{a}$ $\bigg| \sqrt{}$

$x= \pm \sqrt{-\frac{c}{a}}$ .

Willst du beispielsweise 4x^2-36=0 berechnen, so erhältst du als Ergebnis

$4x^2=36 \quad \quad \quad \quad \quad \bigg| \div 4$

x^2 = 9

$x_{1,2} = \pm \sqrt{9} = \pm 3$ .

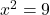
Quadratische Gleichungen lösen: ax²+bx=0

Für quadratische Gleichungen der Form ax²+bx=0 bietet sich das Ausklammern von x an. Dann kannst du die Nullstellen beider Faktoren einzeln berechnen.

ax²+bx=0

x(ax+b)=0

x₁=0 und

$ax+b=0 \Longleftrightarrow ax = -b$

$x_2=-\frac{b}{a}$ .

Damit kannst du beispielsweise die quadratische Gleichung x²+4x=0 lösen, indem du x zuerst ausklammerst

x(x+4)=0.

Dann siehst du sofort, dass x₁=0 und x₂=-4 gelten muss.

Quadratische Gleichungen lösen: ax²+bx+c=0

im Videozur Stelle im Video springen

Für eine quadratische Gleichung der Form ax²+bx+c=0 gibt es verschiedene Lösungsformeln und Ansätze, die wir nachfolgend kurz erklären. Zu jedem dieser Themen findest du auch einen ausführlichen Artikel verlinkt.

Allgemein kann eine quadratische Gleichung keine, eine oder zwei Lösungen haben. Das ist von der Diskriminante abhängig, das heißt von dem Ausdruck, der bei den Lösungsformeln unter der Wurzel steht. Dabei unterscheidet sich die Diskriminante von der pq Formel nicht wesentlich von der Diskriminante der Mitternachtsformel, sie lassen sich für a=1 ineinander umformen.

Diskriminante der Lösungsformeln:

Mitternachtsformel: D=b^2-4ac

pq Formel: $D=\left(\frac{p}{2}\right)^2-q$

D>0: die quadratische Gleichung hat zwei Lösungen
D=0: Die quadratische Gleichung hat eine Lösung
D<0: Die quadratische Gleichung hat keine Lösung

pq Formel

Quadratische Gleichungen in Normalform löst du am besten mit der pq Formel .

pq Formel

$x^2+p\cdot x +q = 0 \quad \Longleftrightarrow \quad x_{1,2} = -\frac{p}{2}\pm \sqrt{\left(\frac{p}{2}\right)^2-q}$

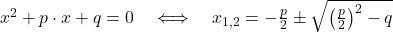
Betrachten wir dafür ein Beispiel und lösen die Gleichung

x²+10x+25=0.

Da sie schon in Normalform vorliegt, können wir p=10 und q = 25 direkt ablesen und in die pq Formel einsetzen

$x_{1,2} = -\cfrac{10}{2} \pm \sqrt{\left(\frac{10}{2}\right) ^2-25} =-5 \pm \sqrt{5^2-25} = -5 \pm 0 = -5$ .

Die Lösungsmenge besteht in diesem Fall nur aus einem Element $\mathbb{L}=\{-5\}$ .

Mitternachtsformel und abc-Formel

Willst du quadratische Gleichungen lösen, die in ihrer allgemeinen Form vorliegen, so bietet sich die Verwendung der Mitternachtsformel an. Sie wird manchmal auch als abc Formel bezeichnet.

Mitternachtsformel / abc Formel

$ax^2 +bx+c=0 \quad \Longleftrightarrow \quad x_{1,2} = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

Ein Beispiel hierfür ist die Berechnung der Lösungsmenge der quadratischen Gleichung

2x^2-6x = 8 .

Dazu bringen wir die Gleichung zuerst auf ihre allgemeine Form:

2x^2-6x-8=0 .

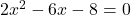Als nächstes bestimmen wir die Parameter a=2, b=-6 und c=-8, die wir in die Mitternachtsformel einsetzen.

$x_{1,2} = \cfrac{-(-6)\pm \sqrt{(-6)^2-4\cdot 2 \cdot (-8)}}{2\cdot 2}$

$= \cfrac{6 \pm \sqrt{36+64}}{4}$

$= \cfrac{6 \pm \sqrt{100}}{4}$

$= \cfrac{6 \pm 10}{4}$

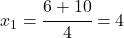$x_1 = \cfrac{6+10}{4}=4$ und $x_2 =\cfrac{6-10}{4}=-1$

Nun müssen wir nur noch die Lösungsmenge $\mathbb{L}=\{-1; 4\}$ aufschreiben.

Satz von Vieta

im Videozur Stelle im Video springen

Um besonders schöne, ganzzahlige quadratische Gleichungen lösen zu können, wendet man oft auch den Satz von Vieta an:

Satz von Vieta

Die beiden Lösungen x₁und x₂der quadratischen Gleichung x²+px+q=0 lassen sich berechnen durch

(I) x₁ + x₂= -p und (II) x₁ · x₂= q

Ein typisches Beispiel, wie du mit Vieta quadratische Gleichungen lösen kannst, ist

x²+3x-4=0.

Dazu stellen wir zuerst ein lineares Gleichungssystem auf

(I) x₁ + x₂= -3

(II) x₁ · x₂= -4,

und sehen sofort, dass in diesem Fall x₁ = 1 und x₂= -4 gelten muss.

Quadratische Ergänzung

In vielen Fällen ist es sehr nützlich, quadratische Funktionen von ihrer Allgemeinen Form in die Scheitelpunktform umzuwandeln. Dazu benötigst du die quadratische Ergänzung , bei der du die quadratische Gleichung auf eine binomische Formel zurückführst.

Auch das zeigen wir dir am besten am Beispiel 2x^2-20x+60 . Hier haben wir den Vorfaktor 2 gegeben, den wir zuerst ausklammern

$2\left(x^2-10x\right)+60.$

Das negative Vorzeichen verrät, dass wir die zweite binomische Formel mit a=x und b=5 verwenden müssen.

$2\left(x^2-10x\right)+60 = 2 \left(x^2-2 \cdot 5 x \right) +60.$

Diesen Term ergänzen wir im nächsten Schritt quadratisch mit +5^2-5^2 und erhalten

$2\left( x^2-2 \cdot 5 x + \underbrace{5^2 - 5^2}_{=0} \right) +60$

$=2\left( ( x^2-2 \cdot 5 x +5^2 )- 5^2\right) +60$

$=2\left( x-5\right)^2 -50 +60$

$=2\left(x-5\right)^2+10.$

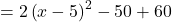
Quadratische Gleichungen Aufgaben

Nun zeigen wir dir verschiedene Aufgaben mit Lösungen zu quadratischen Gleichungen.

Aufgabe 1: Quadratische Gleichungen lösen mit Mitternachtsformel oder pq Formel

a) x²+2x=-1

b) $\frac{1}{2}x^2+2x+5=0$ .

Aufgabe 2: Quadratische Gleichungen lösen mit Vieta

Löse die quadratische Gleichung x²-2x-15=0 unter Verwendung des Satzes von Vieta.

Aufgabe 3: Quadratische Gleichungen lösen durch Ausklammern oder Wurzel ziehen

a) x²=2x

b) 2 x²-18=0

Lösung

Aufgabe 1: Quadratische Gleichungen lösen mit Mitternachtsformel oder pq Formel

a) Um die quadratische Gleichung x²+2x=-1 zu lösen verwenden wir hier am besten die pq Formel. Dazu bringen wir sie zuerst auf Normalform

x²+2x+1=0.

Nun setzen wir p=2 und q=1 in die pqFormel ein

$x_{1,2} =- \frac{2}{2} \pm \sqrt{\left(\frac{2}{2}\right)^2-1} = -1 \pm \sqrt{1-1} = -1\pm 0$ .

Wir erhalten somit eine ein-elementige Lösungsmenge $\mathbb{L}=\{-1\}$ .

b) Willst du diese quadratische Gleichung lösen, bietet sich die Verwendung der Mitternachtsformel an.

$\frac{1}{2}x^2+2x+5=0$ .

Setzen wir $a=\frac{1}{2}$ , b=2 und c=5 in die Mitternachtsformel ein, so erhalten wir

$x_{1,2} = \cfrac{-2\pm \sqrt{2^2-4\cdot \frac{1}{2} \cdot 5}}{2\cdot \frac{1}{2}}$

$= \cfrac{-2\pm \sqrt{4-10}}{1}$

$= -2 \pm \sqrt{-6}$

Da die Wurzelfunktion nicht für negative Zahlen definiert ist, hat diese Gleichung kein Ergebnis!

Aufgabe 2: Quadratische Gleichungen lösen mit Vieta

Um x²-2x-15=0 zu berechnen, stellen wir zuerst das Gleichungssystem auf

(I) x₁ + x₂= 2

(II) x₁ · x₂= -15.

Durch scharfes Anschauen der zweiten Gleichung siehst du, dass nur die Wertepaare 1 und -15, -1 und 15, 3 und -5 oder -3 und 5 infrage kommen. Betrachtest du nun die erste Gleichung, ist sofort klar, dass x₁=-3 und x₂= 5 sein muss.

Aufgabe 3: Quadratische Gleichungen lösen durch Ausklammern oder Wurzel ziehen

a) Um x²=2x aufzulösen, formen wir die Gleichung so um, dass auf der rechten Seite eine Null steht und klammern daran anschließend aus.

x²– 2x = 0

x (x – 2) = 0.

Damit sind die beiden Lösungen hier x₁ = 0 und x₂= 2.

b) 2x²-18=0 lässt sich durch einfache Äquivalenzumformungen und Wurzel ziehen lösen

2x²– 18 = 0

2x²= 18

x²= 9

$x_{1,2}=\pm\sqrt{9} = \pm 3$ .

Quadratische Ergänzung

Super! Du hast nun einige Methoden zum Lösen quadratischer Gleichungen kennengelernt. Manchmal ist es hilfreich eine Funktion mit der quadratischen Ergänzung in die Scheitelpunktform oder eine binomische Formel umzuwandeln. Schau dir also auf jeden Fall unser Video dazu an um zukünftig alle Gleichungen problemlos lösen zu können!

quadratische Ergänzung, quadratisch ergänzen, Quadratische Ergänzung Formel — Zum Video: Quadratische Ergänzung

zur Videoseite: Quadratische Gleichungen

Beliebte Inhalte aus dem Bereich Algebra

Gleichungen umstellen

Lineare Gleichungen

Gleichungen lösen

Quadratische Gleichungen

Satz vom Nullprodukt

Intervall Mathe

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .