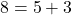Lineare Gleichungen
In diesem Beitrag erklären wir dir, was lineare Gleichungen sind und wie du sie lösen kannst. Du möchtest dich beim Lernen lieber entspannt zurücklehnen? Dann schau dir einfach unser Video zum Thema an!
Inhaltsübersicht
Was sind lineare Gleichungen?
Lineare Gleichungen erkennst du daran, dass nur ein einfaches x vorkommt. Das x wird Variable genannt. Hier siehst du einige Beispiele für lineare Gleichungen.
Die folgenden Beispiele sind keine linearen Gleichungen, weil das x mit einer Hochzahl oder gar nicht vorkommt.
Dabei kannst du alle linearen Gleichungen durch Umformen in diese Form bringen.

Für a und b können beliebige Zahlen eingesetzt werden. Nur a=0 ist nicht erlaubt, denn sonst käme in der Gleichung ja kein x mehr vor.
Beispiel 1
Lass uns das einmal gemeinsam an einem Beispiel für lineare Gleichungen durchgehen.

Schritt 1: Zuerst bringst du alle Zahlen ohne ein x auf eine Seite der Gleichung. Dafür rechnest du auf beiden Seiten der Gleichung +1. Damit fällt die -1 links weg und rechts rechnest du 8+1=9.

Schritt 2: Jetzt teilst du noch die gesamte Gleichung durch den Faktor 3, der vor x steht. Damit bekommst du links 3:3=1 und rechts 9:3=3.

Damit hast du die Gleichung nach x aufgelöst. Das bedeutet, dass die Gleichung für x = 3 erfüllt ist. Du kannst das überprüfen, indem du den Wert in die lineare Gleichung einsetzt und schaust, ob beide Seiten der Gleichung dasselbe Ergebnis haben.

Hinweis: Das Vorgehen, wenn du auf beiden Seiten der Gleichung die gleiche Rechnung durchführst, findest du auch unter dem Namen Äquivalenzumformung.
Beispiel 2
Machen wir doch gleich noch ein weiteres Beispiel. Diesmal sollst du die folgende lineare Gleichung lösen.

Schritt 1: Zunächst musst du die Klammern auflösen. Das funktioniert durch das Ausmultiplizieren, du rechnest dabei beide Teile der Klammer mal ein halb. Im Anschluss daran kannst du die Teile ohne x zusammenfassen -2+10=8.

Schritt 2: Nun bringst du die 8 auf die rechte Seite der Gleichung, indem du auf beiden Seiten – 8 rechnest. Links fällt dann die 8 weg, 8-8=0 und rechts hast du dann 0-8=-8. Dann stehen alle Bausteine ohne x auf einer Seite und alle Teile mit einem x auf der anderen Seite.

Schritt 3: Zum Schluss teilst du die ganze lineare Gleichung wieder durch den Faktor vor dem x. In diesem Beispiel bedeutet das, dass du die Gleichung mit Zwei multiplizierst.

Damit hast du ein Ergebnis für x erhalten. Mit diesen Schritten kannst du alle linearen Gleichungen lösen.
Lineare Gleichungen Aufgaben
Hier findest du zwei Aufgaben zu linearen Gleichungen , mit denen du üben kannst.
Aufgabe 1
Löse die Gleichung
 .
.
Lösung Aufgabe 1
Zuerst bringst du alle Teile der Gleichung mit einem x auf eine Seite und alle Zahlen ohne x auf die andere Seite der Gleichung. Dann kannst du die lineare Gleichung umformen und x bestimmen.

Aufgabe 2
Löse die lineare Gleichung
 .
.
Lösung Aufgabe 2

Lineare Gleichungen — häufigste Fragen
(ausklappen)
Lineare Gleichungen — häufigste Fragen
(ausklappen)-
Woran erkenne ich, ob eine Gleichung linear ist?Eine Gleichung ist linear, wenn nur ein einfaches x vorkommt, also ohne Hochzahl. Dann steht die Variable x nur in der ersten Potenz, zum Beispiel in „3x-1=8” oder „5x=10”. Nicht linear sind Gleichungen wie „7x²=5” oder „x³-2x=1”.
-
Warum darf bei der Form
 die Zahl a nicht 0 sein?
Bei
die Zahl a nicht 0 sein?
Bei darf a nicht 0 sein, weil sonst gar kein x mehr vorkommt. Wenn
darf a nicht 0 sein, weil sonst gar kein x mehr vorkommt. Wenn  wäre, bliebe nur
wäre, bliebe nur  übrig, und das wäre keine lineare Gleichung mit Variable x, die du nach x lösen kannst.
übrig, und das wäre keine lineare Gleichung mit Variable x, die du nach x lösen kannst.
-
Wie mache ich aus einer linearen Gleichung eine Form, wo nur noch x alleine steht?Du stellst x frei, indem du zuerst alle Zahlen ohne x auf eine Seite bringst und danach durch den Faktor vor x teilst. Dabei rechnest du auf beiden Seiten immer das Gleiche. Aus „3x-1=8” wird so erst „3x=9” und dann „x=3”.
-
Wie löse ich eine lineare Gleichung mit Klammern und einem Bruch vor dem x?Du löst zuerst die Klammer durch Ausmultiplizieren und fasst danach die Zahlen zusammen. Dann bringst du die Zahl ohne x auf die andere Seite und entfernst zum Schluss den Bruchfaktor vor x durch Multiplizieren. Bei
 erhältst du so am Ende
erhältst du so am Ende  .
.
-
Wie kann ich mein Ergebnis für x am Ende schnell überprüfen?Du überprüfst dein Ergebnis, indem du den gefundenen x-Wert in die Ausgangsgleichung einsetzt und beide Seiten ausrechnest. Stimmen linke und rechte Seite überein, ist die Lösung korrekt. Bei „3x-1=8” und
 ergibt sich links
ergibt sich links  und rechts 8.
und rechts 8.
Quadratische Gleichungen
Das Lösen linearer Gleichungen stellt für dich nun kein Problem mehr dar. Aber was machst du, wenn in einer Gleichung ein x² vorkommt?
- 3x² + 5x + 2 = 0
- 12x² + 7x = 0
- 6x² – 10 = 0
Solche Gleichungen mit der Hochzahl 2 heißen quadratische Gleichungen. Welche Arten von quadratischen Gleichungen es gibt und wie du sie löst, erfährst du in unserem Video dazu! Viel Spaß beim Anschauen!