Potenzgleichungen

Potenzgleichungen einfach erklärt

Eine Potenzgleichung hast du immer dann, wenn die Variable in einer Gleichung eine Hochzahl hat. Sie nennst du auch Exponent. Eine einfache Potenzgleichung kann also so aussehen:

x⁴ = 16

Alle Zahlen, die du für x einsetzen kannst und für die die Gleichung stimmt, sind dann Lösungen für die Gleichung. 

Du kannst durch Ausprobieren herausfinden, welcher Wert für x eingesetzt werden muss. Eine schnellere Lösung bekommst du allerdings, wenn du nach x auflöst. Um die Potenz auflösen zu können, musst du immer die Wurzel ziehen: 

x³ = 64       |
x   =  
x   = 4

Eine Potenzgleichung hat dabei entweder zwei, eine oder keine Lösung.

Potenzgleichungen mit geraden Exponenten

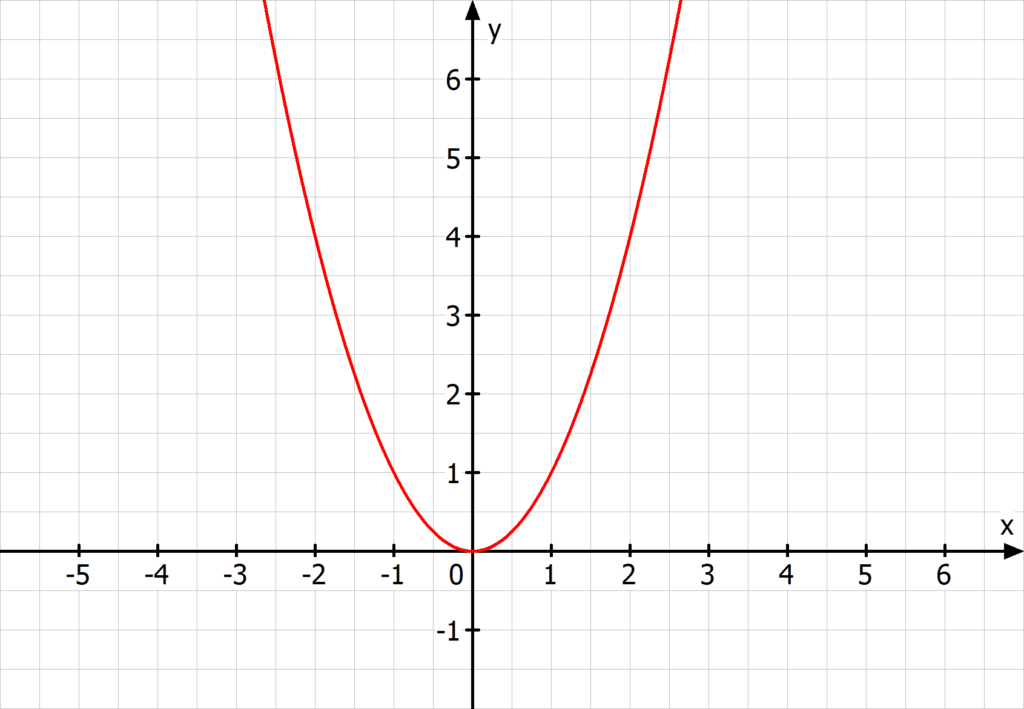
Potenzgleichungen, die eine gerade Potenz haben, sehen als Graph wie eine Parabel aus. Je nach Vorzeichen und Hochzahl ändern sich lediglich die Eigenschaften der Parabel . Hier siehst du das Beispiel f(x)=x².

direkt ins Video springen

Es gibt drei mögliche Arten von Potenzgleichungen mit geraden Exponenten: Das b in der Gleichung kann eine positive, eine negative Zahl oder eine Null sein. 

b positiv 

Als Beispiel für das Potenzgleichung Lösen hast du die folgende Gleichung:

x⁴ = 16 |
x   =
x   = 2  ✅

Du musst aber bedenken, dass hier auch eine negative Zahl rauskommen kann. Denn (-2)⁴ ergibt genauso 16. Das liegt an der geraden Potenz, die das Minuszeichen verschwinden lässt. Ausgeschrieben wäre das nämlich:

(-2) · (-2) · (-2) · (-2) = 16

Die Ergebnisse sind also x = -2 und +2. Unser Beispiel hat also zwei Lösungen.

b negativ 

Schau dir zu den geraden Potenzen direkt noch ein Beispiel an, wo b negativ ist: 

x² = – 25  |
x   =  ❌ 

Das Auflösen nach x ist hier nicht möglich. Denn jede negative Zahl verliert mit einer geraden Potenz ihr Minuszeichen. Beispielsweise wäre (-5)² also 25 und nicht -25.
Die Potenzgleichung hat hier also keine Lösung.

b = 0 

Eine Potenzgleichung mit geraden Exponenten hat nur eine Lösung, wenn b in der Gleichung 0 ist:

 x² = 0

Hier wäre die eine Lösung für x folglich 0. 

Potenzgleichungen mit ungeraden Exponenten

Bei Potenzgleichungen mit ungeradem Exponenten funktioniert das Potenz Auflösen wie bei geraden Exponenten. Auch hier unterscheidest du wieder, ob b eine positive, negative Zahl oder eine Null ist.

b positiv 

Schau dir dazu direkt ein Beispiel an: 

x³ = 27 |
x    =
x    = 3   ✅ 

Im Gegensatz zum Potenzgleichung Lösen mit gerader Hochzahl haben die mit ungeraden Exponenten immer nur eine Lösung. Hier ergibt -3 eingesetzt nämlich -27. Das Minus verschwindet nicht und nur eine Lösung ist somit richtig. 

b negativ 

Dass das Minus nicht verschwindet, siehst du auch am folgenden Beispiel mit einem negativen b:

x⁵ + 8  = -24  | -8
x⁵        = -32  |
x          =
x          = -2   ✅

Genauso ist hier auch nur eine Lösung richtig. Denn (+2)⁵ wäre nämlich +32.

b = 0 

Eine Potenzgleichung mit ungerader Hochzahl kann also immer nur eine Lösung haben, auch wenn b gleich 0 ist. Dann wäre die Lösung nämlich 0. Im Gegensatz zu den geraden Exponenten kann es hier aber auch nie keine Lösung geben. 

Komplexere Potenzfunktionen

Das Prinzip der Berechnung bleibt bei allen Potenzgleichungen gleich. Es können trotzdem noch andere Aufgaben, wie Zusammenfassen oder Ausmultiplizieren beim Lösen von Gleichungen mit Hochzahlen dazu kommen. Rechne dazu auch noch zwei weitere Beispiele: 

x⁴ + 4x⁴  = 80  | Zusammenfassen
5x⁴          = 80  | :5 
x⁴            = 16  |
x              =
x              = 2 und -2 ✅

Selbst wenn die Gleichung erst einmal kompliziert aussieht, kannst du durch Umformen auf die normale Form einer Potenzgleichung kommen. Das siehst du auch an dem Beispiel:

4 · (2x² – 3) = -44  | Ausmultiplizieren 
8x² – 12       = -44  | +12
8x²               = -32   | : 8
x²                 = -4    |
x                   =   ❌

Potenzgleichungen — häufigste Fragen 

• Was ist eine Potenzgleichung? 
  Eine Potenzgleichung ist eine Gleichung, bei der die Variable eine Hochzahl hat. So wird sie auch Potenz genannt. Sie könnte beispielsweise so aussehen: x⁴ = 16.
  
  
• Wie viele Lösungen kann eine Potenzgleichung haben? 
  Eine Potenzgleichung mit gerader Hochzahl kann zwei, eine oder keine Lösung haben. Dahingegen haben Gleichungen mit ungerader Hochzahl immer nur eine Lösung.

Negative Potenzen 

Klasse! Jetzt weißt du, wie du Potenzgleichungen lösen kannst. Natürlich kann es aber vorkommen, dass die Potenz selbst negativ ist. Wenn du auch das meistern willst, schau in unser Video über die negativen Potenzen rein!