Video

Quiz

Hier geht's zum Video „pq Formel“

Mitternachtsformel einfach erklärt

Wichtige Inhalte in diesem Video

Mitternachtsformel Beispiel

a, b und c bestimmen

Mitternachtsformel Übungen: Gleichung mit einer Lösung

Mit der Mitternachtsformel kannst du schnell und einfach quadratische Gleichungen lösen. Hier und in unserem Video lernst du die Mitternachtsformel mit Übungen und Beispielen kennen!

Inhaltsübersicht

Mitternachtsformel einfach erklärt

Die Mitternachtsformel ist eine Lösungsformel für quadratische Gleichungen der Form ax² + bx + c = 0. Die drei Zahlen, die an den Stellen von a, b und c stehen, setzt du einfach in die Formel ein.

Mitternachtsformel

$x_{1,2} = \cfrac{- \textcolor{blue}{b} \pm \sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a} \textcolor{olive}{c}}}{2 \textcolor{red}{a}}$

a ist die Zahl vor dem x²
b ist die Zahl vor dem x
c ist die Zahl ohne x

Das ± heißt, dass du zweimal rechnest: einmal mit dem + vor der Wurzel und einmal mit dem – vor der Wurzel. Oft hast du also zwei Lösungen.

Aufgepasst: Wenn unter der Wurzel eine negative Zahl rauskommt, hat die Gleichung überhaupt keine Lösung!

Mitternachtsformel Beispiel

im Videozur Stelle im Video springen

Mit der Mitternachtsformel kannst du also Gleichungen mit x hoch 2 auflösen. Schau dir ein Beispiel dazu an:

$\textcolor{red}{2}x^2+\textcolor{blue}{6}x + \textcolor{olive}{4}$

Schritt 1: Bestimme a, b und c.

a = 2, b = 6 und c = 4

Schritt 2: Setze a, b und c in die Mitternachtsformel ein.

$x_{1,2} = \cfrac{- \textcolor{blue}{6} \pm \sqrt{\textcolor{blue}{6}^2-4\cdot \textcolor{red}{2} \cdot \textcolor{olive}{4}}}{2 \cdot \textcolor{red}{2}} = \cfrac{-6 \pm \sqrt{4}}{4} = \cfrac{-6 \pm 2}{4}$

Schritt 3: Rechne die Lösung einmal mit + und einmal mit – aus.

Lösung mit „+„: $x_1 = \cfrac{-6 \boldsymbol{+} 2}{4} = -1$

Lösung mit „–„: 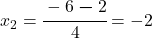$x_2 = \cfrac{-6 \boldsymbol{-} 2}{4} = -2$

Die beiden Lösungen der Gleichung sind also x₁ = -1 und x₂ = -2.

a, b und c bestimmen

im Videozur Stelle im Video springen

Manchmal kannst du a, b und c für die Lösungsformel nicht so einfach ablesen. Dann helfen dir folgende Regeln:

Wenn vor x² oder x keine Zahl steht ⇒ a = 1 oder b = 1

x² + 2x – 1 ⇒ a = 1, b = 2, c = -1

Wenn vor x² oder x nur ein Minus steht⇒ a = -1 oder b = -1

3x²– x – 1 ⇒ a = 3, b = -1, c = -1

Wenn es keine Zahl ohne x gibt ⇒ c = 0

3x² – x ⇒ a = 3, b = -1, c = 0

Mitternachtsformel Übungen: Gleichung mit einer Lösung

im Videozur Stelle im Video springen

Schau dir noch weitere Mitternachtsformel Übungen an. Du willst folgende Gleichung mit x hoch 2 auflösen: $\textcolor{red}{\frac{1}{3}} x^2\textcolor{blue}{-2}x+\textcolor{olive}{3} =0$

Schritt 1: Bestimme a, b und c (auf negative Vorzeichen achten!).

a = 1/3, b = –2 und c = 3

Schritt 2: Setze die Zahlen in die Lösungsformel für die quadratische Gleichung ein.

$x_{1,2} = \cfrac{- \textcolor{blue}{(-2)} \pm \sqrt{\textcolor{blue}{(-2)}^2-4\cdot \textcolor{red}{\frac{1}{3}} \cdot \textcolor{olive}{3}}}{2 \cdot \textcolor{red}{\frac{1}{3}}} = \cfrac{2 \pm \sqrt{4-4}}{\frac{2}{3}} = \cfrac{2 \pm 0}{\frac{2}{3}}$

Schritt 3: Unter der Wurzel steht eine 0. Deshalb gibt es nur eine Lösung. Du kannst also mit + oder mit – weiterrechnen — es kommt bei beidem das Gleiche heraus.

$\cfrac{2 + 0}{\frac{2}{3}} = 3$

Die Lösung der quadratischen Gleichung ist also x = 3.

Mitternachtsformel Übungen: Gleichung ohne Lösung

Löse $x^2+\textcolor{blue}{4}x+\textcolor{olive}{10}=0$ .

Schritt 1: Bestimme a, b und c.

a = 1, b = 4 und c = 10

Schritt 2: Setze die Zahlen in die Lösungsformel für die quadratische Gleichung ein.

$x_{1,2} = \cfrac{-\textcolor{blue}{4}\pm \sqrt{\textcolor{blue}{4}^2-4\cdot \textcolor{red}{1} \cdot \textcolor{olive}{10}}}{2\cdot \textcolor{red}{1}} = \cfrac{-4\pm \sqrt{16-40}}{2} = \cfrac{-4\pm \sqrt{-24}}{2}$

Unter der Wurzel steht eine negative Zahl. Deshalb hat die quadratische Gleichung keine Lösung.

Merke: Anzahl der Lösungen

Unter der Wurzel positive Zahl ⇒ zwei Lösungen
Unter der Wurzel 0 ⇒ eine Lösung
Unter der Wurzel negative Zahl ⇒ keine Lösung

Den Teil unter der Wurzel nennst du übrigens auch Diskriminante .

Mitternachtsformel Beispiel: Gleichung umstellen

Wenn auf keiner Seite der Gleichung eine 0 steht, musst du die Gleichung zuerst umstellen. Schau dir ein Beispiel an:

$\textcolor{red}{\frac{1}{2}}x^2+\textcolor{olive}{30} = \textcolor{blue}{8}x$

Hier bringst du die 8x zuerst auf die andere Seite.

$\begin{align*} \textcolor{red}{\frac{1}{2}}x^2+\textcolor{olive}{30} &= \textcolor{blue}{8}x \qquad |-\textcolor{blue}{8}x \\ \textcolor{red}{\frac{1}{2}}x^2 \textcolor{blue}{-8x}+ \textcolor{olive}{30} &= 0 \end{align*}$

Das löst du dann wie vorher mit der Mitternachtsformel.

Mitternachtsformel – kurz & knapp

Mit der Mitternachtsformel kannst du die Lösung von quadratischen Gleichungen (ax² + bx + c = 0) berechnen.

Schritt 1: Bestimme a, b und c.
Schritt 2: Setze a, b und c in die Mitternachtsformel ein.
Schritt 3: Rechne die Lösung einmal mit + und einmal mit – aus.

Expertenwissen: Mitternachtsformel Herleitung

Hinweis: Noch mehr Details erfährst du in unserem Experten-Video zur Mitternachtsformel !

Für die Mitternachtsformel Herleitung löst du nur die allgemeine quadratische Gleichung nach x auf.

$\begin{align*} ax^2+bx+c&=0 \enspace &|& -c \\ ax^2+bx&=-c \enspace &|& : a \\ x^2+\cfrac{b}{a}x &= -\cfrac{c}{a} \end{align*}$

Um an dieser Stelle weiterrechnen zu können, benötigst du die quadratische Ergänzung der linken Seite.

$x^2+\frac{b}{a}x +\left(\frac{b}{2a}\right)^2= -\frac{c}{a} + \left(\frac{b}{2a}\right)^2$

$x^2+\frac{b}{a}x +\left(\frac{b}{2a}\right)^2= -\frac{c}{a} + \frac{b^2}{4a^2}$

Die rechte Seite fasst du für die Mitternachtsformel Herleitung noch weiter zusammen, indem du $-\frac{c}{a}$ mit erweiterst und die Terme dann auf einen Bruchstrich schreibst.

$x^2+\cfrac{b}{a}x +\left(\cfrac{b}{2a}\right)^2= \cfrac{b^2-4ac}{4a^2}$

Auf der linken Seite hält sich eine binomische Formel versteckt, sodass du diesen Term auch umformen kannst zu

$\left(x+\cfrac{b}{2a}\right)^2= \cfrac{b^2-4ac}{4a^2}$ .

Davon ziehst du nun die Wurzel und erhältst

$x+\cfrac{b}{2a} =\pm \sqrt{\cfrac{b^2-4ac}{4a^2}}$

Vereinfachen und Subtraktion von $\frac{b}{2a}$ ergibt schon fast die quadratische Formel (Mitternachtsformel):

$x = -\cfrac{b}{2a}\pm \sqrt{\cfrac{b^2-4ac}{4a^2}}$

$x = -\cfrac{b}{2a}\pm \cfrac{\sqrt{b^2-4ac}}{2a}$

$\Rightarrow x_{1,2} = \cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Merke: Dass wir stattdessen x_1 und x_2 und $\pm$ schreiben, sorgt dafür, dass du die zweite Lösung nicht vergisst!

Mitternachtsformel — häufigste Fragen

Was ist die Mitternachtsformel?
Die Mitternachtsformel ist eine Formel, mit der du die Lösungen einer quadratischen Gleichung der Form ax² + bx + c = 0 berechnen kannst. Die Mitternachtsformel lautet: x = (-b ± √(b² – 4ac)) ÷ 2a. Das ± bedeutet, dass du die Formel einmal mit Plus und einmal mit Minus berechnen musst. Du bekommst daher zwei Werte: x₁ und x₂.
Was ist A, B und C bei der Mitternachtsformel?
In der Mitternachtsformel sind A, B und C die Zahlen (Koeffizienten) der quadratischen Gleichung ax² + bx + c = 0: A ist die Zahl vor x², B die Zahl vor x und C ist die Konstante — also die Zahl ohne x.

Quiz zum Thema Mitternachtsformel einfach erklärt

pq Formel

Bei manchen quadratischen Gleichungen ist es einfacher, die pq Formel zu verwenden. Schau dir gleich unser Video dazu an, um zu verstehen, wie sie funktioniert!

Zum Video: pq Formel

zur Videoseite: Mitternachtsformel einfach erklärt

Beliebte Inhalte aus dem Bereich Algebra

Quadratische Gleichungen lösen

Mitternachtsformel einfach erklärt

Mitternachtsformel

pq Formel einfach erklärt

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .