Quadratische Gleichungen lösen
Quadratische Gleichungen lösen kannst du auf viele verschiedene Arten. Hier und im Video zeigen wir dir an vielen Beispielen, wie du quadratische Gleichungen lösen kannst!
Inhaltsübersicht
Quadratische Gleichungen lösen
Quadratische Gleichungen in der Normalform x2 + px + q = 0 löst du mithilfe der pq-Formel:
![Rendered by QuickLaTeX.com \[\mathbf{x_{1,2}=-\cfrac{\textcolor{red}{p}}{2}\pm\sqrt{\left(\cfrac{\textcolor{red}{p}}{2}\right)^2-\textcolor{blue}{q}}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-262d241817c96db89facd57fc6a02280_l3.png)
Hast du zum Beispiel x2 + 8x – 20 = 0, setzt du nun einfach p = 8 und q = –20 in die pq-Formel ein:

Du bekommst also die Lösung:
![Rendered by QuickLaTeX.com \[x_{1}=2\quad x_{2}=-10\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e6301918436e9b7e025bfe1d123388df_l3.png)
Wichtig: Die pq-Formel funktioniert nur, wenn du eine Gleichung in der Normalform gegeben hast. Sieht deine Funktion anders aus, benutzt du andere Verfahren, die wir uns jetzt anschauen.
Reinquadratische Gleichungen lösen
Quadratische Gleichungen, in denen nur ein x2 und kein einzelnes x steht, nennst du reinquadratische Gleichungen. Du kannst sie mithilfe der Wurzel lösen. Schau dir dazu das Beispiel an:
x2 = 25
Wenn du die Lösung der quadratischen Gleichung bestimmen willst, ziehst du die Wurzel:
x2 = 25 | √
![Rendered by QuickLaTeX.com \[\textcolor{red}{x_{1,2}}=\pm\sqrt{\textcolor{blue}{25}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8c5d819927e0971fece9fbb88725b6ce_l3.png)
Das  vor der Wurzel bedeutet, dass es zwei Lösungen gibt, eine positive und eine negative Lösung:
vor der Wurzel bedeutet, dass es zwei Lösungen gibt, eine positive und eine negative Lösung:
x1 = +5
x2 = -5
Merke: Beim Wurzelziehen hast du also immer zwei Lösungen für x, eine positive und eine negative!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Quadratische Gleichungen lösen Ausklammern
Hast du eine Gleichung ohne eine Zahl mit x (Restglied), fehlt dir also das q von der Normalform. Hier kannst du die Gleichung mit Ausklammerns lösen:
x2 – 5x = 0 | x ausklammern
x · (x – 5) = 0
Im nächsten Schritt verwendest du den Satz vom Nullprodukt . Eine Malaufgabe ist nämlich insgesamt gleich null, wenn nur ein Teil von ihr Null ist. Also gibt es hier zwei mögliche Lösungen:
x1 = 0
x2 – 5 = 0
Also ist die erste Lösung der Gleichung schonmal 0 und bei der zweiten Gleichung erhältst du die Lösung durch Umformen:
x2 – 5 = 0 | + 5
x2 = 5
Deine zweite Lösung ist also gleich 5.
Quadratische Gleichungen lösen abc Formel
Wenn eine Zahl vor dem x2 steht, kannst du die abc Formel (Mitternachtsformel) benutzen:
![Rendered by QuickLaTeX.com \[x_{1,2}=\cfrac{-\textcolor{red}{b}\pm\sqrt{\textcolor{red}{b}^2-4\textcolor{olive}{a}\textcolor{blue}{c}}}{2\textcolor{olive}{a}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70ded905ce066e2c8d84c3056aecfe52_l3.png)
Damit löst du eine quadratische Gleichung in der folgenden Form:
ax2 + bx + c = 0
Schau dir als Beispiel diese Gleichung an:
4x2 + 32x+ 64 = 0
Um die quadratische Gleichung zu lösen, setzt du für a = 4, für b = 32 und für c = 64 in die abc-Formel ein:

Du hast in dem Beispiel nur eine Lösung, weil unter der Wurzel eine Null steht. x ist also gleich -4.
Merke: Anwendung findet das Lösen von quadratischen Gleichungen meistens bei quadratischen Funktionen zur Berechnung der Nullstellen .
Wie viele Lösungen gibt es bei quadratischen Gleichungen?
Es gibt grundsätzlich drei verschiedene Möglichkeiten, was die Anzahl der Lösungen bei quadratischen Gleichungen angeht:
Zwei Lösungen
Normalerweise erhältst du zwei Lösungen. Das liegt daran, dass es zwei Zahlenwerte gibt, die quadriert x² sein können. Denn sowohl positive als auch negative Zahlen zum Quadrat ergeben ein positives Ergebnis.
x² = 36
sowohl 6² als auch (-6)² ergibt 36
Eine Lösung
Es gibt die Situation, da kommst du bei der Lösung der quadratischen Gleichung auf nur ein Ergebnis. Das passiert, wenn in der Wurzel eine Null steht. Das Ergebnis von 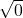 ist immer nur Null, da 0 • 0 = 0.
ist immer nur Null, da 0 • 0 = 0.
x² – 4x + 4 = 0
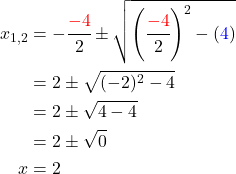
Keine Lösung
Außerdem kann es vorkommen, dass du überhaupt keine Lösung bekommst. Das passiert, wenn du in der Rechnung eine Wurzel aus einer negativen Zahl ziehen sollst, also zum Beispiel  . Diese Rechnung ist nicht möglich, da keine Zahl quadriert eine negative Zahl ergeben kann. Deswegen sagst du, dass die Lösungsmenge der Gleichung leer ist:
. Diese Rechnung ist nicht möglich, da keine Zahl quadriert eine negative Zahl ergeben kann. Deswegen sagst du, dass die Lösungsmenge der Gleichung leer ist: 
Quadratische Gleichungen lösen — häufigste Fragen
(ausklappen)
Quadratische Gleichungen lösen — häufigste Fragen
(ausklappen)-
Wann nutze ich die pq-Formel und wann die abc-Formel?Du verwendest die pq-Formel, wenn die Gleichung die Form x² + px + q = 0 hat (also a = 1). Steht vorne ein anderer Faktor, also a ≠ 1, nutze die abc-Formel.
-
Was ist die Diskriminante und was sagt sie aus?Die Diskriminante lautet Δ = b² − 4ac (bei ax² + bx + c = 0). Gilt Δ > 0, gibt es zwei reelle Lösungen; Δ = 0 liefert genau eine; Δ < 0 keine reellen (nur komplexe). In der pq-Schreibweise entspricht das (p/2)²-q.
-
Wie erkenne ich die Anzahl der Lösungen am Graphen?
Der Graph von y = ax² + bx + c ist eine Parabel. Schneidet sie die x-Achse zweimal, hat sie zwei Lösungen. Wenn sie die x-Achse nur berührt, hat sie eine Lösung und wenn der Graph die x-Achse überhaupt nicht berührt oder schneidet, gibt es gar keine Lösungen. -
Was passiert, wenn unter der Wurzel keine „schöne“ Zahl steht?
Wenn du die Wurzel nicht perfekt auflösen kannst, lass den Wurzelterm am besten so stehen wie er ist. Alternativ kannst du auch die Dezimalnäherung verwenden.
Satz von Vieta
Jetzt kennst du verschiedene Möglichkeiten quadratische Gleichungen zu lösen. Wenn du einen coolen Zusammenhang zwischen der Lösung von quadratischen Gleichungen sehen willst, ist der Satz von Vieta genau das Richtige für dich. Schau dir doch gleich unser Video dazu an.
