Produkt Mathe

Produkt in Mathe einfach erklärt

im Videozur Stelle im Video springen

(00:13)

Ein Produkt in Mathe ist:

1. Das Ergebnis einer Multiplikation .
2. Der Term der Multiplikation, also die Rechnung selbst. 

Formal kannst du sagen: Ein Produkt in der Mathematik ist eine Abbildung • von den Mengen A × B in die Menge C:

• : A × B → C

(a, b) ↦ a • b = c

Du ordnest somit zwei Elementen a ∈ A und b ∈ B ihr Produkt c ∈ C zu. Die beiden Elemente a und b heißen dabei Faktoren.

Schau dir gleich an, welche unterschiedlichen Arten von Produkten es gibt! Einen Überblick dazu findest du auch in unserem Video !

Produkte von Zahlen

im Videozur Stelle im Video springen

(00:42)

Das Produkt von zwei Zahlen ist selbst wieder eine Zahl. Außerdem sind Produkte von Zahlen assoziativ . Für a aus A, b aus B und d aus einer dritten Menge D ist also

(a • b) • d = a • (b • d)

Oft betrachtest du Produkte von Zahlen aus der gleichen Menge, zum Beispiel von zwei natürlichen Zahlen. Du hast also A = B. Dann liegt auch dein Ergebnis wieder in derselben Menge — es ist also sogar A = B = C. Schau dir das gleich an verschiedenen Zahlenmengen an!

Produkt von natürlichen Zahlen

Das Produkt von zwei natürlichen Zahlen kannst du dir an einem Brett mit Spielsteinen vorstellen, die in Reihen und Spalten angeordnet sind. Die Anzahl der Steine auf dem Brett ist das Produkt der Anzahl der Reihen (r) und der Anzahl der Spalten (s).

direkt ins Video springen

Um r • s zu berechnen, kannst du also

• die Anzahl der Steine in einer Reihe (= Anzahl der Spalten s) so oft addieren, wie es Reihen gibt (r)
• die Anzahl der Steine in einer Spalte (= Anzahl der Reihen r) so oft addieren, wie es Spalten gibt (s)

     

Es ist somit egal, ob du erst die Zeilen oder erst die Spalten betrachtest — die Multiplikation von natürlichen Zahlen ist also kommutativ .

Übrigens: Das Produkt von 0 und einer beliebigen Zahl ist immer 0.

Produkt von ganzen Zahlen

Wenn du zu den natürlichen Zahlen noch die negativen Zahlen hinzufügst, erhältst du die ganzen Zahlen . Um das Produkt von zwei ganzen Zahlen zu berechnen, multiplizierst du zunächst ihre Beträge . Dann schreibst du das richtige Vorzeichen davor:

Beispiel: (-2) • 5 = -10, weil |-2| • |5| = 2 • 5 = 10 und – mal + gleich – ist.

Übrigens: Anders als die natürlichen Zahlen bilden die ganzen Zahlen einen sogenannten Ring. Du findest also immer inverse Elemente bezüglich der Addition (z.B. 2 und -2), aber nicht unbedingt bezüglich der Multiplikation. Zum Beispiel ist 2 eine ganze Zahl, aber ihr Inverses ½ nicht. 

Produkt von rationalen Zahlen

In den ganzen Zahlen kannst du eine Zahl nicht durch jede andere Zahl teilen. Anders ist das bei rationalen Zahlen , also den Brüchen . Hier kannst du alle Grundrechenarten ausführen, solange du nicht durch 0 teilst. Das Produkt von zwei Brüchen ist dann:

   

Übrigens: Weil du in den rationalen Zahlen ohne Einschränkung addieren , subtrahieren, multiplizieren und dividieren kannst (außer Division durch 0), bilden sie einen sogenannten Körper. 

Produkt von reellen Zahlen

Nicht jede Zahl lässt dich durch einen Bruch darstellen. Bei der Kreiszahl π oder bei beispielsweise geht das nicht. Sie sind also nicht rational, sondern irrational. Die rationalen und irrationalen Zahlen zusammen bilden die reellen Zahlen .

Was ist das Produkt von zwei irrationalen Zahlen?

Jede irrationale Zahl hat unendlich viele Nachkommastellen, zum Beispiel π = 3,1415… und = 1,1424… Wenn du nur endlich viele Nachkommastellen betrachtest, kannst du leicht das Produkt bilden, zum Beispiel 3,14 • 1,14.

Jetzt erhöhst du nach und nach die Anzahl der Nachkommastellen. So kommst du immer näher an das tatsächliche Produkt der beiden irrationalen Zahlen heran. Du bildest also immer bessere rationale Näherungswerte. 

Produkt von komplexen Zahlen

Es gibt Gleichungen , die sich mit reellen Zahlen nicht lösen lassen, zum Beispiel x² = -1. Um hier trotzdem eine Lösung zu ermitteln, brauchst du komplexe Zahlen . Eine komplexe Zahl hat allgemein die Form a + bi, wobei ist. Dabei sind a und b reelle Zahlen.

Das Produkt von zwei komplexen Zahlen berechnest du dann durch einfaches Ausmultiplizieren : 

(a + bi) · (c + di) = a·c + a·di + b·ci + b·d·i² = (ac – bd) + (ad + bc)i

Beachte dabei, dass i² = -1 ergibt.

Produkt in der linearen Algebra

im Videozur Stelle im Video springen

(02:46)

In der linearen Algebra geht es um Vektorräume V und lineare Abbildung zwischen Vektorräumen. Dabei kannst du dir verschiedene Produkte anschauen:

• Skalarprodukt
• Kreuzprodukt
• Spatprodukt
• Produkt von Matrizen

Skalarprodukt

Das Skalarprodukt ∘ bildet zwei Vektoren auf eine reelle Zahl ab. Es ist also eine Abbildung

∘ : V × V → ℝ

In einem n-dimensionalen Euklidischen Raum (z.B. im ℝⁿ) gilt dabei die Formel:

   

Beispiel im ℝ³:

Das Skalarprodukt hat einige interessante Eigenschaften:

• Es gilt immer v ∘ v > 0 für alle v ≠ 0, v ∈ V.
• Das Skalarprodukt ist bilinear.
• Es hängt mit dem Betrag eines Vektor (Norm) zusammen, nämlich .
• Du kannst damit den Winkel φ zwischen zwei Vektoren v und w ausrechnen:

     

Kreuzprodukt im ℝ³

Das Kreuzprodukt × brauchst du vor allem in der analytischen Geometrie. Es bildet zwei Vektoren aus dem ℝ³ auf einen weiteren Vektor aus dem ℝ³ ab: 

× : ℝ³ × ℝ³ → ℝ³

Die Formel dafür lautet:

   

Das Kreuzprodukt in der Mathematik hat zwei wichtige Eigenschaften:

• Antikommutativität: v × w = –w × v für v ∈ ℝ³ und w ∈ ℝ³
• v × v = 0 für v ∈ ℝ³

Spatprodukt im ℝ³

Das Spatprodukt det ist ein Produkt von drei Vektoren im ℝ³:

det: ℝ³ × ℝ³ × ℝ³ → ℝ

Du berechnest es, in dem du die drei Vektoren nebeneinander in eine Matrix schriebst und ihre Determinante ermittelst. Das machst du zum Beispiel mit der Regel von Sarrus .

Beispiel: Spatprodukt von , und :

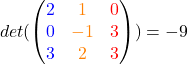
Das Spatprodukt heißt so, weil du damit das Volumen eines Spats im ℝ³ berechnen kannst. Ein Spat ist ein schiefer Quader.

Produkt von Matrizen

Eine Matrix mit r Zeilen und s Spalten kannst du allgemein als A = (a_i,j)_{i=1,…,r; j=1,…,s} aufschreiben.  

Das Produkt von zwei Matrizen A und B kannst du nur bilden, wenn die Anzahl der Spalten von A gleich der Anzahl der Zeilen von B ist. Also A = (a_i,j)_{i=1,…,r; j=1,…,s} und B = (a_j,k)_{j=1,…,s; k=1,…,t^.} Dann ist: 

   

Übrigens: Quadratische Matrizen bilden mit der Matrixmultiplikation sogar einen Ring.

Produkt in kommutativen Ringen

im Videozur Stelle im Video springen

(04:09)

Nicht immer hast du in Mathe ein Produkt von zwei Zahlen, Vektoren oder Matrizen. Du kannst nämlich auch andere Mengen betrachten und darin Produkte berechnen. Besonders wichtig sind Produkte in sogenannten kommutativen Ringen. Schau dir das an zwei Beispielen an.

Restklassenringe

Schau dir erstmal an, was Restklassenringe überhaupt sind: 

• Stell dir dazu vor, du teilst eine ganze Zahl durch 2. Dann bekommst du entweder den Rest 0 (wenn die Zahl gerade ist), oder den Rest 1 (wenn die Zahl ungerade ist).
• Jetzt teilst du eine ganze Zahl durch 3. Dann bekommst du entweder Rest 0 (z.B. bei 6), Rest 1 (z.B. bei 7) oder Rest 2 (z.B. bei 8).

Allgemein gibt es bei der Division durch n immer n mögliche Reste. Alle Zahlen, die den gleichen Rest haben, fasst du in einer sogenannten Restklasse zusammen. Du sprichst dann von einer Restklasse modulo n.

Beispiel: Restklassen modulo 3
Du hast die 3 Restklassen 0, 1 und 2. Du schreibst sie meistens 0 + 3ℤ, 1 + 3ℤ und 2 + 3ℤ.

Allgemein hat eine Restklasse modulo n also immer die Form a + nℤ. Die Menge aller Restklassen modulo n nennst du den Restklassenring ℤ/nℤ. Es ist also ℤ/3ℤ = {0 + 3ℤ, 1 + 3ℤ, 2 + 3ℤ}

Jetzt kannst du das Produkt von Restklassen bilden: 

(a + nℤ) · (b + nℤ) = a · b + nℤ

Beispiel: (1 + 3ℤ) · (2 + 3ℤ) = 1 · 2 + 3ℤ = 2 + 3ℤ

Übrigens: Teilweise (aber nicht immer!) gibt es zu einer Restklasse a + nℤ eine Restklasse b + nℤ, sodass (a + nℤ) · (b + nℤ) = 1 + nℤ ist. Dann hat a ein multiplikatives Inverses in ℤ/nℤ. Du findest es mit dem euklidischen Algorithmus . Wenn n eine Primzahl ist, gibt es sogar immer ein solches Inverses.

Polynomringe

Ein Polynom kannst du allgemein in der Form  schreiben. Die Menge aller Polynome mit Koeffizienten aus den reellen Zahlen ℝ und mit Variable X bezeichnest du mit ℝ[X]. Die Menge bildet einen Ring. Innerhalb von ℝ[X] kannst du das Produkt von zwei Polynomen bilden: 

   

mit

   

Endliche und unendliche Produkte

Jetzt weißt du schon ziemlich viel darüber, was Produkt in Mathe bedeutet. Schau dir zum Schluss noch an, wie du ein Produkt in der Mathematik vereinfacht aufschreiben kannst!

Endliches Produkt in Mathe

Wenn ein Produkt in Mathematik zwar endlich ist, aber sehr viele Faktoren hat, kannst du das Produktzeichen Π als abgekürzte Schreibweise verwenden.

Beispiel – Fakultät : n! = n · (n-1) · … · 2 · 1. Anstatt „…“ kannst du auch die Produktschreibweise verwenden:

   

Das Produktzeichen funktioniert also genauso wie ein Summenzeichen . Allgemein kannst du einen beliebigen Term a_k in das Produktzeichen schrieben, der von k abhängt:

   

Übrigens: Das  ist ein großes Pi und stehst für den Anfangsbuchstaben von Produkt.

Unendliches Produkt in Mathe

Das Produktzeichen eignet sich auch für eine Produkt in Mathe mit unendlich viele Faktoren. Beispiel:

   

So ein unendliches Produkt in Mathe konvergiert, wenn drei Bedingungen erfüllt sind:

1. Es existiert ein k₀, sodass a_k ≠ 0 für alle k > k₀. Ab einem bestimmten k₀ sind also alle a_k ungleich 0.
2. Der Grenzwert

      

   existiert, ergibt also eine reelle Zahl.
3. Der Grenzwert ist nicht 0.

Das Produkt

   

beispielsweise konvergiert, denn kein Faktor ist gleich 0 und es gilt: 

   

Übrigens: Die Faktoren eines konvergenten Produkt in Mathe müssen immer gegen 1 konvergieren. Ansonsten konvergiert das Produkt nicht.

Produkt von Mengen

Du kannst auch das Produkt von zwei Mengen A und B bilden. Es heißt kartesisches Produkt A × B. Einem Element a ∈ A und einem Element b ∈ B ordnest du dabei das Paar (a, b) zu. 

Das kartesische Produkt in Mathe wirkt vielleicht zunächst nicht wie ein Produkt, weil du keine Elemente verrechnest. Du kannst das Produkt hier aber allgemein als eine Art Verbindung von Elementen sehen.

Mengenlehre

Du kannst nicht nur Produkte von Mengen bilden, sondern auch beispielsweise Schnittmengen oder Vereinigungsmengen. Wenn sich das interessiert, dann schau doch gleich bei unserem Video zur Mengenlehre vorbei!