Drehmatrix
Mit der Drehmatrix kannst du Vektoren im Raum um einen bestimmten Winkel drehen. Wenn du wissen willst, wie das funktioniert, schau dir doch den Artikel oder unser Video an.
Inhaltsübersicht
Drehmatrix einfach erklärt
Mit einer Drehmatrix oder auch Rotationsmatrix  kannst du einen Vektor um den Winkel
kannst du einen Vektor um den Winkel  gegen den Uhrzeigersinn drehen. Rotationsmatrizen sind orthogonal.
Ihre Determinante
hat außerdem den Wert von +1.
gegen den Uhrzeigersinn drehen. Rotationsmatrizen sind orthogonal.
Ihre Determinante
hat außerdem den Wert von +1.
Im  sieht die Drehmatrix
sieht die Drehmatrix  wie folgt aus:
wie folgt aus:

![Rendered by QuickLaTeX.com \[\textcolor{blue}{R_{\alpha}}=\textcolor{blue}{\left(\begin{array}{cc}cos\left(\alpha\right)&-sin\left(\alpha\right)\\sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3f557a086b4c56ab2a76462922b87102_l3.png)
Multiplizierst
du die Drehmatrix mit einem Vektor  und setzt für
und setzt für  zum Beispiel 60° ein, drehst du den Vektor um 60° im Koordinatensystem:
zum Beispiel 60° ein, drehst du den Vektor um 60° im Koordinatensystem:
![Rendered by QuickLaTeX.com \[\textcolor{blue}{R_{60^\circ}}=\textcolor{blue}{\left(\begin{array}{cc}cos\left(60^\circ\right)&-sin\left(60^\circ\right)\\sin\left(60^\circ\right)&cos\left(60^\circ\right)\\\end{array}\right)}\quad\overrightarrow{v}=\left(\begin{array}{c}1\\0\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e199435bc8a793d6d458c6ec9313e879_l3.png)
![Rendered by QuickLaTeX.com \[\textcolor{blue}{R_{60^\circ}} \cdot \overrightarrow{v }= \textcolor{blue}{\left(\begin{array}{cc}cos\left(60^\circ\right)&-sin\left(60^\circ\right)\\sin\left(60^\circ\right)&cos\left(60^\circ\right)\\\end{array}\right)} \cdot \left(\begin{array}{c}1\\0\end{array}\right)=\left(\begin{array}{c}\textcolor{blue}{cos\left(60^\circ\right)}\cdot1\textcolor{blue}{-sin\left(60^\circ\right)}\cdot0\\\textcolor{blue}{sin\left(60^\circ\right)}\cdot1+\textcolor{blue}{cos\left(60^\circ\right)}\cdot0\end{array}\right)=\left(\begin{array}{c}cos\left(60^\circ\right)\\sin\left(60^\circ\right)\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}0,5\\\frac{\sqrt{3}}{2}\end{array}\right)}=\textcolor{red}{\overrightarrow{v_{2}}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dc161816efa75a9c99c927b73b0a4ee4_l3.png)
Merke: Möchtest du deinen Vektor im Uhrzeigersinn drehen, musst du den Vektor mit der Inversen der Drehmatrix multiplizieren.
![Rendered by QuickLaTeX.com \[R^{-1}_{\alpha}=\left(\begin{array}{cc}cos\left(\alpha\right)&sin\left(\alpha\right)\\-sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a52a936cc080fb363ce9b13496a87b2_l3.png)
Drehmatrix R3
Die Drehmatrix gibt es natürlich auch im  . Allerdings musst du hier aufpassen: Im
. Allerdings musst du hier aufpassen: Im  kannst du deinen Vektor um die x1-,x2 –oder x3 -Achse drehen.
kannst du deinen Vektor um die x1-,x2 –oder x3 -Achse drehen.
Deine Rotationsmatrizen sehen dann jeweils so aus:
|
R3 |
x1 -Koordinate ( |
x2 -Koordinate ( |
x3 -Koordinate ( |
| Drehmatrix | |
|
|
Wenn du den Vektor  um 90° um die x1 -Achse drehen willst, benötigst du die Rotationsmatrix
um 90° um die x1 -Achse drehen willst, benötigst du die Rotationsmatrix  :
:
![Rendered by QuickLaTeX.com \[\overrightarrow{v_{1}}=\left(\begin{array}{c}0\\2\\3\end{array}\right)\quad R_{x_{1}}\left(\alpha\right)=\textcolor{olive}{\left(\begin{array}{ccc}1&0&0\\0&cos\left(\alpha\right)&-sin\left(\alpha\right)\\0&sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-629110e30006353a598a2cb68eb0c981_l3.png)
Dann setzt du 90° für  in deiner Drehmatrix ein und multiplizierst sie mit dem Vektor
in deiner Drehmatrix ein und multiplizierst sie mit dem Vektor  . Bei der Matrixmultiplikation
multiplizierst du für den ersten Eintrag wieder die erste Zeile der Matrix mit der Spalte des Vektors. Für den zweiten Eintrag musst du dann die zweite Zeile der Matrix mit der Spalte des Vektors mal nehmen und für den dritten Eintrag dann die dritte Zeile der Drehmatrix mit der Spalte des Vektors:
. Bei der Matrixmultiplikation
multiplizierst du für den ersten Eintrag wieder die erste Zeile der Matrix mit der Spalte des Vektors. Für den zweiten Eintrag musst du dann die zweite Zeile der Matrix mit der Spalte des Vektors mal nehmen und für den dritten Eintrag dann die dritte Zeile der Drehmatrix mit der Spalte des Vektors:
![Rendered by QuickLaTeX.com \[\textcolor{olive}{R_{x_{1}}\left(90^\circ\right)}\overrightarrow{v_{1}}=\textcolor{olive}{\left(\begin{array}{ccc}1&0&0\\0&cos\left(90^\circ\right)&-sin\left(90^\circ\right)\\0&sin\left(90^\circ\right)&cos\left(90^\circ\right)\\\end{array}\right)}\left(\begin{array}{c}0\\2\\3\end{array}\right) =\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-505a0d7875d46784c3fec0030b5c9b8d_l3.png)
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}1\cdot0+0\cdot2+0\cdot3\\0\cdot0+cos\left(90^\circ\right)\cdot2-sin\left(90^\circ\right)\cdot3\\0\cdot0+sin\left(90^\circ\right)\cdot2+cos\left(90^\circ\right)\cdot3\end{array}\right)=\left(\begin{array}{c}0\\0\cdot2-1\cdot3\\1\cdot2+0\cdot3\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}0\\-3\\2\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd744a10f749c19ebfb7beb1b5c48296_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
1.Beispiel:
Drehe den Vektor  um 30° gegen den Uhrzeigersinn.
um 30° gegen den Uhrzeigersinn.
![Rendered by QuickLaTeX.com \[\overrightarrow{v}=\left(\begin{array}{c}1\\3\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0980dbe58467f3415209ce4fee9d7953_l3.png)
Lösung:
Dafür benötigst du deine Drehmatrix aus dem  . Wenn du deine Drehmatrix berechnen möchtest, setzt du 30° für
. Wenn du deine Drehmatrix berechnen möchtest, setzt du 30° für  ein. Dann multiplizierst du diese mit deinem Vektor
ein. Dann multiplizierst du diese mit deinem Vektor  . Wenn du Matrizen multiplizieren
willst, rechnest du immer Zeile mal Spalte. Die erste Zeile deiner Drehmatrix wird mit der Spalte deines Vektors multipliziert. So erhältst du den ersten Eintrag deines rotierten Vektors
. Wenn du Matrizen multiplizieren
willst, rechnest du immer Zeile mal Spalte. Die erste Zeile deiner Drehmatrix wird mit der Spalte deines Vektors multipliziert. So erhältst du den ersten Eintrag deines rotierten Vektors  . Für den zweiten Eintrag musst du die zweite Zeile deiner Rotationsmatrix mit der Spalte deines Vektors multiplizieren:
. Für den zweiten Eintrag musst du die zweite Zeile deiner Rotationsmatrix mit der Spalte deines Vektors multiplizieren:
![Rendered by QuickLaTeX.com \[R_{30^\circ} \cdot \overrightarrow{v}=\left(\begin{array}{cc}cos\left(30^\circ\right)&-sin\left(30^\circ\right)\\sin\left(30^\circ\right)&cos\left(30^\circ\right)\\\end{array}\right) \cdot \left(\begin{array}{c}1\\3\end{array}\right)=\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5c59d2a5eaa96132c778a5879f5142d5_l3.png)
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}cos\left(30^\circ\right)\cdot1-sin\left(30^\circ\right)\cdot3\\sin\left(30^\circ\right)\cdot1+cos\left(30^\circ\right)\cdot3\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}cos\left(30^\circ\right)-3sin\left(30^\circ\right)\\sin\left(30^\circ\right)+3cos\left(30^\circ\right)\end{array}\right)}=\textcolor{red}{v_{2}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5811fe7167f5ae97b8bb82e015ccaa8d_l3.png)
Drehmatrix R2 Herleitung
Die Drehmatrix lässt sich im  gut mit Hilfe des Einheitskreises herleiten:
gut mit Hilfe des Einheitskreises herleiten:
Zuerst betrachtest du den Einheitsvektor e1 :
Diesen versuchst du um den Winkel  zu drehen. Dafür kannst du den Einheitskreis
benutzen. An diesem drehst du den Vektor gegen den Uhrzeigersinn:
zu drehen. Dafür kannst du den Einheitskreis
benutzen. An diesem drehst du den Vektor gegen den Uhrzeigersinn:
Wenn du den Einheitsvektor e1 am Einheitskreis um den Winkel  gegen den Uhrzeigersinn drehen möchtest, ergibt sich der neue Vektor:
gegen den Uhrzeigersinn drehen möchtest, ergibt sich der neue Vektor:
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}cos\left(\alpha\right)\\sin\left(\alpha\right)\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a43b67180f00f84dbe76a23b079e7bae_l3.png)
Jetzt kannst du dir das Gleiche noch bei dem Einheitsvektor e2 anschauen:
Der neue Vektor lautet dann:
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}-sin\left(\alpha\right)\\cos\left(\alpha\right)\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aa3fd131197bfff44b862063cf0b62fb_l3.png)
Du kannst mit der Linearkombination der beiden Einheistvektoren jeden Vektor bilden. Das bedeutet, dass du durch die gleiche Linearkombination mit den beiden gedrehten Einheitsvektoren um den Winkel  den gedrehten Vektor bekommst. Schau dir dazu den Vektor
den gedrehten Vektor bekommst. Schau dir dazu den Vektor  an:
an:
![Rendered by QuickLaTeX.com \[\overrightarrwo{v}=\left(\begin{array}{c}2\\4\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-15b0203f6205e35f09fd5c63487673a8_l3.png)
Dieser setzt sich aus zweimal dem Einheitsvektor  und viermal dem Einheitsvektor
und viermal dem Einheitsvektor  zusammen:
zusammen:
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}2\\4\end{array}\right)=2\overrightarrow{e_{1}}+4\overrightarrow{e_{2}}=2\cdot \left(\begin{array}{c}1\\0\end{array}\right)+4\cdot\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}2\\0\end{array}\right)+\left(\begin{array}{c}0\\4\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd9e64e0c077468b4f261f0b17a01477_l3.png)
Möchtest du den Vektor  um den Winkel
um den Winkel  drehen, kannst du einfach das zweifache des ersten gedrehten Einheitsvektors mit dem vierfachen des zweiten gedrehten Einheitsvektors addieren:
drehen, kannst du einfach das zweifache des ersten gedrehten Einheitsvektors mit dem vierfachen des zweiten gedrehten Einheitsvektors addieren:
![Rendered by QuickLaTeX.com \[\overrightarrow{v*}=2\cdot\left(\begin{array}{c}cos\left(\alpha\right)\\sin\left(\alpha\right)\end{array}\right)+4\cdot\left(\begin{array}{c}-sin\left(\alpha\right)\\cos\left(\alpha\right)\end{array}\right)=\left(\begin{array}{c}2cos\left(\alpha\right)-4sin\left(\alpha\right)\\2sin\left(\alpha\right)+4cos\left(\alpha\right)\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-71c61ddb63f686849e04da7f1bd38798_l3.png)
Das ist aber das gleiche, als wenn du den Vektor  einfach mit der Drehmatrix multiplizieren würdest:
einfach mit der Drehmatrix multiplizieren würdest:
![Rendered by QuickLaTeX.com \[R_{\alpha}\overrightarrow{v}=\left(\begin{array}{cc}cos\left(\alpha\right)&-sin\left(\alpha\right)\\sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)\left(\begin{array}{c}2\\4\end{array}\right)=\left(\begin{array}{c}2cos\left(\alpha\right)-4sin\left(\alpha\right)\\2sin\left(\alpha\right)+4cos\left(\alpha\right)\end{array}\right)=\overrightarrow{v*}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-53a7fdc222658192057dac9a1a225b0c_l3.png)
Du siehst also, dass die erste Spalte der Rotationsmatrix genau den x-Anteil des gedrehten Vektors bestimmt und die zweite Zeile den y-Anteil.
Drehmatrix R3 Beispiele
Schau dir zum Schluss noch die Drehmatrix im  an.
an.
2.Beispiel:
Drehe den Vektor  um 180° um die x1 -Achse.
um 180° um die x1 -Achse.
![Rendered by QuickLaTeX.com \[\overrightarrow{v_{1}}=\left(\begin{array}{c}0\\4\\2\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f13e75d331bb3bfab72b7a82c6434697_l3.png)
Lösung:
Damit du den Vektor um die x1 -Achse drehen kannst, brauchst du die Drehmatrix  . Für
. Für  setzt du dann 180° ein und multiplizierst diese mit dem Vektor
setzt du dann 180° ein und multiplizierst diese mit dem Vektor  . Für die Einträge deines neuen Vektors
. Für die Einträge deines neuen Vektors  rechnest du dann wieder Zeile mal Spalte und erhältst:
rechnest du dann wieder Zeile mal Spalte und erhältst:
![Rendered by QuickLaTeX.com \[R_{x_{1}} \cdot \left(180^\circ\right)\overrightarrow{v_{1}}=\textcolor{olive}{\left(\begin{array}{ccc}1&0&0\\0&cos\left(180^\circ\right)&-sin\left(180^\circ\right)\\0&sin\left(180^\circ\right)&cos\left(180^\circ\right)\\\end{array}\right)} \cdot \left(\begin{array}{c}0\\4\\2\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}0\\-4\\-2\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-21fb334237cf25f023b2d9528d62c7e6_l3.png)
Arten der Drehung
Du darfst beim Rechnen mit Rotationsmatrizen nicht vergessen, dass es zwei verschiedene Arten von Drehungen gibt.
Aktive Drehung
Bei einer aktiven Drehung drehst du den Vektor gegen den Uhrzeigersinn. Das bedeutet du verwendest für die Rotation Matrix  :
:
![Rendered by QuickLaTeX.com \[R_{\alpha}=\left(\begin{array}{cc}cos\left(\alpha\right)&-sin\left(\alpha\right)\\sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aa63dd26da348ff783788355559f62a0_l3.png)
Merke: Bei der aktiven Drehung verwendest du immer die Drehmatrix  .
.
Passive Drehung
Bei einer passiven Drehung drehst du das Koordinatensystem. Das ist gleichbedeutend, als wenn du deinen Vektor im Uhrzeigersinn drehen würdest. Du verwendest für die Rotation dafür die Inverse der Drehmatrix:
![Rendered by QuickLaTeX.com \[R^{-1}_{\alpha}=\left(\begin{array}{cc}cos\left(\alpha\right)&sin\left(\alpha\right)\\-sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a52a936cc080fb363ce9b13496a87b2_l3.png)
Merke: Bei der passiven Drehung verwendest du immer die Inverse der Drehmatrix  .
.
Matrizenmultiplikation
Wie du gesehen hast, musst du, um die Drehmatrix überhaupt anwenden zu können, ganz schön fit in Matrizenmultiplikation sein. Wenn du das nochmal üben möchtest, schau dir doch direkt unser Video dazu an!

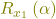 )
) )
) )
)![Rendered by QuickLaTeX.com \[\textcolor{olive}{\left(\begin{array}{ccc}1&0&0\\0&cos\left(\alpha\right)&-sin\left(\alpha\right)\\0&sin\left(\alpha\right)&cos\left(\alpha\right)\\\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-30a31e536b7f9e9ea355f0094db4e3f4_l3.png)
![Rendered by QuickLaTeX.com \[\textcolor{olive}{\left(\begin{array}{ccc}cos\left(\alpha\right)&0&sin\left(\alpha\right)\\0&1&0\\-sin\left(\alpha\right)&0&cos\left(\alpha\right)\\\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-11b1db8ecc53bc3d6330b05fefb683fc_l3.png)
![Rendered by QuickLaTeX.com \[\textcolor{olive}{\left(\begin{array}{ccc}cos\left(\alpha\right)&-sin\left(\alpha\right)&0\\sin\left(\alpha\right)&cos\left(\alpha\right)&0\\0&0&1\\\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e56d857a6ea51c683d3f7bc10de2434b_l3.png)


![Rendered by QuickLaTeX.com \[ \overrightarrow{v_{1}}=\left(\begin{array}{c}1\\9\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b3fcf5aca2d08f31bfea8f5e3c05f384_l3.png)
 . Du musst für
. Du musst für ![Rendered by QuickLaTeX.com \[R^{-1}_{60^\circ} \cdot \overrightarrow{v_{1}}=\left(\begin{array}{cc}cos\left(60^\circ\right)&sin\left(60^\circ\right)\\-sin\left(60^\circ\right)&cos\left(60^\circ\right)\\\end{array}\right) \cdot \left(\begin{array}{c}1\\9\end{array}\right)=\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3aac48b4b9855fcea7b377be7975c09a_l3.png)
![Rendered by QuickLaTeX.com \[\left(\begin{array}{c}cos\left(60^\circ\right)\cdot1+sin\left(60^\circ\right)\cdot9\\-sin\left(60^\circ\right)+cos\left(60^\circ\right)\end{array}\right)=\left(\begin{array}{c}\frac{1}{2}\cdot1+\frac{\sqrt{3}}{2}\cdot9\\\-\frac{\sqrt{3}}{2}\cdot1+\frac{1}{2}\cdot9\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}\frac{1+9\sqrt{3}}{2}\\\frac{9-\sqrt{3}}{2}\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a01cb946d62832b64771fd5f7c9a1993_l3.png)




![Rendered by QuickLaTeX.com \[\overrightarrow{v_{1}}=\left(\begin{array}{c}0\\2\\6\end{array}\right)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6e55e609034d358c7a856ce25b89412e_l3.png)
![Rendered by QuickLaTeX.com \[R_{x_{1}}\left(45^\circ\right) \cdot \overrightarrow{v_{1}}=\textcolor{olive}{\left(\begin{array}{ccc}1&0&0\\0&cos\left(45^\circ\right)&-sin\left(45^\circ\right)\\0&sin\left(45^\circ\right)&cos\left(45^\circ\right)\\\end{array}\right)} \cdot \left(\begin{array}{c}0\\2\\6\end{array}\right)=\textcolor{red}{\left(\begin{array}{c}0\\-2\sqrt{2}\\4\sqrt{2}\end{array}\right)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a5d02b3ed2c3e9732331c894e66efb14_l3.png)


