Matrizen multiplizieren
Für die Multiplikation von Matrizen gibt es ein ganz einfaches Berechnungsschema. Hier zeigen wir dir, wie es funktioniert und was du für die Matrixmultiplikation alles wissen musst.Das Berechnungsschema lässt sich in einem Video anschaulicher erklären. Schaue gleich mal rein!
Inhaltsübersicht
Matrixmultiplikation einfach erklärt
Die Matrizenmultiplikation bzw. Matrixmultiplikation bezeichnet die multiplikative Verknüpfung zweier Matrizen, dessen Ergebnis Produktmatrix heißt.
Du darfst zwei Matrizen multiplizieren, wenn die Spaltenanzahl der ersten Matrix A gleich der Zeilenanzahl in der zweiten Matrix B ist. Dabei multiplizierst du nacheinander jede Zeile der Matrix A mit jeder Spalte der Matrix B. Wenn du eine 
mit einer 
multiplizierst, ist die Produktmatrix eine 
.
Matrizen multiplizieren
Eine anschauliche Möglichkeit zwei Matrizen zu multiplizieren ist das Falk-Schema. Wie rechnest du zum Beispiel das Matrixprodukt 
von
![\[ \textbf{A} = \begin{pmatrix} 1 & 2 & 1 \\ 3 & 1 & 4 \\ 1 & 5 & 2 \end{pmatrix} \quad\text{und}\quad \textbf{B} = \begin{pmatrix} 2 & 3 \\ 4 & 1 \\ 1 & 1 \end{pmatrix} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-17f3932bf79c78516ebb18e4fceb7426_l3.png "Rendered by QuickLaTeX.com")
aus? Beim Falk-Schema schreibst du dir deine Matrizen in eine Tabelle. Links steht die erste Matrix A und oben steht die zweite Matrix B. Dabei darfst du nicht vergessen, dass die Anzahl der Spalten von Matrix A gleich der Anzahl der Zeilen von Matrix B sein muss.
![\[ \begin{array}{ccc|cc} & & & \textcolor{red}{2} & \textcolor{blue}{3} \\ \multicolumn{3}{c|}{\textbf{A} \cdot \textbf{B}} & \textcolor{red}{4} & \textcolor{blue}{1} \\ & & & \textcolor{red}{1} & \textcolor{blue}{1} \\\cline{1-5} \textcolor{olive}{1} & \textcolor{olive}{2} & \textcolor{olive}{1} & c_{\textcolor{olive}{1}\textcolor{red}{1}} & c_{\textcolor{olive}{1}\textcolor{blue}{2}} \\ \textcolor{orange}{3} & \textcolor{orange}{1} & \textcolor{orange}{4} & c_{\textcolor{orange}{2}\textcolor{red}{1}} & c_{\textcolor{orange}{2}\textcolor{blue}{2}}\\ \textcolor{teal}{1} & \textcolor{teal}{5} & \textcolor{teal}{2} & c_{\textcolor{teal}{3}\textcolor{red}{1}} & c_{\textcolor{teal}{3} \textcolor{blue}{2}} \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-64b3c1a868eb93cf3d9e592a59dc5098_l3.png "Rendered by QuickLaTeX.com")
Im Falk-Schema kannst du jetzt leicht ablesen, aus welchen Spalten und Zeilen du das Skalarprodukt ermitteln musst, um alle Elemente deiner Produktmatrix auszurechnen.
![\[c_{\textcolor{olive}{1}\textcolor{red}{1}} &= \textcolor{olive}{1}\cdot \textcolor{red}{2} + \textcolor{olive}{2}\cdot \textcolor{red}{4} + \textcolor{olive}{1}\cdot \textcolor{red}{1} = 11\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-15004250f650b27f8f61eb429bf794c2_l3.png "Rendered by QuickLaTeX.com")
Zum Beispiel musst du, um das erste Matrixelement c11 auszurechnen, die erste Zeile von A (olive) und die erste Spalte von B (rot) kombinieren. Um die Zeile und Spalte zu kombinieren, multiplizierst du die ersten Elemente der Zeile und Spalte miteinander (
). Das Ergebnis addierst du zum Produkt der zweiten Elemente der Zeile und Spalte (
) und dem Produkt der dritten Elemente der Zeile und Spalte (
). So einfach funktioniert die Matrizenmultiplikation!
![\[ \textbf{C}=\textbf{A} \cdot \textbf{B} = \begin{pmatrix} 11 & 6 \\ 14 & 14 \\ 24 & 10 \end{pmatrix} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1e4dda8c8b4b8247aa982a280be32dd8_l3.png "Rendered by QuickLaTeX.com")
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Eigenschaften Matrizenmultiplikation
Natürlich gibt es auch beim Matrizenmultiplizieren Regeln. Anders als beim Multiplizieren von Zahlen gilt nicht das Kommutativgesetz. Das bedeutet, du darfst zwei Matrizen A und B bei der Matrixmultiplikation nicht vertauschen.
![\[ \mathbf{A}\cdot\mathbf{B} \neq \mathbf{B}\cdot\mathbf{A} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-02f0f46609d8a81a69e93ce93baa31c2_l3.png "Rendered by QuickLaTeX.com")
Aufgepasst! 
muss nicht definiert sein, nur weil 
definiert ist. Wenn zum Beispiel A eine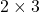 
-Matrix und B eine 
-Matrix ist, kannst du das Matrixprodukt nicht ausrechnen, weil A weniger Zeilen besitzt als B Spalten hat.
Dagegen gilt bei der Matrizenmultiplikation das Distributivgesetz. Das bedeutet, du kannst Matrixmultiplikationen ausklammern und ausmultiplizieren.
![\[ (\mathbf{A}+\mathbf{B})\cdot\mathbf{C}=\mathbf{A}\cdot\mathbf{C}+\mathbf{B}\cdot\mathbf{C} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a9b71cfcad1068d28d97c5cf186a732b_l3.png "Rendered by QuickLaTeX.com")
Außerdem gilt bei der Matrizenmultiplikation das Assoziativgesetz. Das bedeutet, dass die Rechenreihenfolge egal ist, wenn du 3 Matrizen multiplizieren willst.
![\[ (\mathbf{A}\cdot\mathbf{B})\cdot\mathbf{C} = \mathbf{A}\cdot(\mathbf{B}\cdot\mathbf{C}) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-26083c1a7094a220237094af9e410a37_l3.png "Rendered by QuickLaTeX.com")
Inverse Matrix
Die Rechengesetze kennst du schon von dem Multiplizieren von Zahlen. Ein Konzept, das du ebenfalls von dem Multiplizieren von Zahlen kennst, ist der Kehrwert. Multiplizierst du eine Zahl mit ihrem Kehrwert , ist das Ergebnis 1. Bei der Matrizenmultiplikation nennst du den Kehrwert die inverse Matrix und das Ergebnis die Einheitsmatrix. Schaue dir gleich unser passendes Video dazu an!
