Linearkombination
In diesem Artikel erklären wir dir anhand verschiedener Beispiele, was eine Linearkombination ist und wie du sie berechnest. Du möchtest in kürzester Zeit wissen was eine Linearkombination ist? Dann schau dir unser Video dazu an.
Inhaltsübersicht
Linearkombination einfach erklärt
Wenn du einen Vektor mit einer Zahl multiplizierst und dann mit einem anderen Vektor addierst, so erhältst du einen weiteren Vektor. Diesen Vorgang kannst du beliebig oft wiederholen. Dabei nennt man diese Summe von Vektoren Linearkombination.
Jeden Vektor der Form

nennt man Linearkombination der Vektoren  bis
bis  . Wobei
. Wobei 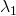 bis
bis  reelle Zahlen sind.
reelle Zahlen sind.
Linearkombination berechnen
Hast du einen Vektor  gegeben, dann lassen sich die Parameter
gegeben, dann lassen sich die Parameter 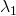 bis
bis  so bestimmen, dass
so bestimmen, dass  sich als Linearkombination von den gegebenen Vektoren
sich als Linearkombination von den gegebenen Vektoren  bis
bis  darstellen lässt.
darstellen lässt.

Damit kannst du das folgende lineare Gleichungssystem aufstellen
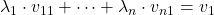


Löst du nun dieses Gleichungssystem, so erhältst du die Werte 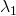 bis
bis  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Betrachten wir ein Beispiel. Angenommen du hast die Vektoren  ,
,  und
und  gegeben, und sollst die Parameter
gegeben, und sollst die Parameter  und
und  bestimmen, sodass sich
bestimmen, sodass sich  als Linearkombination der drei Vektoren
als Linearkombination der drei Vektoren  und
und  darstellen lässt. Du sollst also
darstellen lässt. Du sollst also  und
und  der folgenden Gleichung bestimmen
der folgenden Gleichung bestimmen

Das formst du nun in ein lineares Gleichungssystem um und löst es
(I) 
(II) 
(III) 
Aus (II) siehst du direkt, dass  gelten muss. Einsetzen in (I) liefert dir
gelten muss. Einsetzen in (I) liefert dir 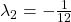 .
. 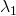 und
und  in (III) einsetzen und du bekommst
in (III) einsetzen und du bekommst  . Somit lässt sich
. Somit lässt sich  also wie folgt als Linearkombination darstellen:
also wie folgt als Linearkombination darstellen:

Lineare Unabhängigkeit von Vektoren
Vektoren  bis
bis  sind genau dann linear unabhängig, wenn sich der Nullvektor nur als Linearkombination der
sind genau dann linear unabhängig, wenn sich der Nullvektor nur als Linearkombination der  bis
bis  darstellen lässt, wenn
darstellen lässt, wenn 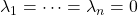 ist.
ist.
Wenn du mehr über lineare Unabhängigkeit und lineare Abhängigkeit von Vektoren erfahren willst, so schau dir unseren Artikel zu diesem Thema an.
Beispiel
Betrachte als Beispiel die Vektoren  ,
,  und
und 
Zuerst stellst du das lineare Gleichungssystem auf
(I) 
(II) 
(III) 
Löst du es, dann siehst du, dass aus (II) folgt  , eingesetzt in (III) ergibt
, eingesetzt in (III) ergibt  und dann folgt aus (I)
und dann folgt aus (I)  . Damit sind die Vektoren
. Damit sind die Vektoren  ,
, 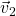 und
und  linear unabhängig.
linear unabhängig.
Linearkombination Spann
Sind die Vektoren  bis
bis  gegeben, so ist der Spann dieser Vektoren, definiert als
gegeben, so ist der Spann dieser Vektoren, definiert als
 .
.
Der Spann  ist also die Menge aller Linearkombinationen der Vektoren
ist also die Menge aller Linearkombinationen der Vektoren  bis
bis  . Das heißt, ist ein Vektor
. Das heißt, ist ein Vektor  , so existieren
, so existieren 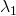 bis
bis  , sodass
, sodass 
Beispiel
Nimmst du zum Beispiel die beiden Vektoren  und
und  , so lassen sich alle Vektoren im
, so lassen sich alle Vektoren im  als Linearkombination von
als Linearkombination von  und
und 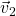 darstellen. Also gilt für den Spann
darstellen. Also gilt für den Spann

Linearkombination Spezialfälle
Im folgenden Abschnitt nennen wir dir spezielle Linearkombinationen, die davon abhängen, wie du die Koeffizienten  wählst.
wählst.
Konische Kombinationen
Hast du eine Linearkombination gegeben, bei dem die Koeffizienten  nur größer oder gleich 0 sind, so heißt die Linearkombination konische Linearkombination.
nur größer oder gleich 0 sind, so heißt die Linearkombination konische Linearkombination.
Graphisch veranschaulicht liegen alle konischen Linearkombinationen zwischen den Vektoren  bis
bis  (blaue Fläche im Bild).
(blaue Fläche im Bild).
Affinkombinationen
Sind die Parameter  einer Linearkombination so gewählt, dass die Summe der
einer Linearkombination so gewählt, dass die Summe der  gleich 1 ergibt, so wird diese Linearkombination Affinkombination genannt.
gleich 1 ergibt, so wird diese Linearkombination Affinkombination genannt.
Konvexkombinationen
Konvexkombinationen sind Linearkombinationen, bei denen die Parameter  zwischen 0 und 1 liegen und deren Summe gleich 1 ergibt.
zwischen 0 und 1 liegen und deren Summe gleich 1 ergibt.
Wenn du dir das Ganze im  veranschaulichst, so liegen alle Konvexkombinationen der Vektoren
veranschaulichst, so liegen alle Konvexkombinationen der Vektoren  und
und  auf der Strecke c, die von den beiden Vektoren
auf der Strecke c, die von den beiden Vektoren  und
und  erzeugt wird.
erzeugt wird.
Weitere Themen der Vektorrechnung
Neben der Linearkombination gibt es noch weitere Themen, die sich mit Vektoren beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:
Linearkombination Aufgaben
Im Folgenden zeigen wir dir zwei Aufgaben mit Lösungen, mit denen du das Berechnen von Linearkombinationen üben kannst.
Aufgabe 1: Linearkombination Vektoren
Du hast die Vektoren  ,
,  und
und 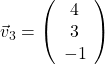 gegeben.
gegeben.
Bestimme die Linearkombination des Vektors  durch die Vektoren
durch die Vektoren  ,
, 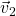 und
und  .
.
Lösung Aufgabe 1
Du suchst also die Werte 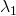 ,
,  und
und  , sodass
, sodass

Dabei erhältst du folgendes lineare Gleichungssystem
(I) 
(II) 
(III) 
Wenn du dir das Ganze nun in einer Matrix aufschreibst,

kannst du diese mit dem Gaußschen Eliminationsverfahren in die Matrix

umformen. Dabei ergibt sich in der dritten Zeile eine Nullzeile. Das heißt, du kannst für  jeden beliebigen Wert wählen, etwa
jeden beliebigen Wert wählen, etwa  . Dementsprechend erhältst du dann
. Dementsprechend erhältst du dann  und
und  .
.
Also lässt sich der Vektor  durch die folgende Linearkombination darstellen
durch die folgende Linearkombination darstellen

Aufgabe 2: Linearkombination Vektoren
Bestimme die Linearkombination des Vektors  durch die Vektoren
durch die Vektoren  ,
,  und
und  .
.
Lösung Aufgabe 2
Du suchst also die Werte 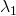 ,
,  und
und  , sodass
, sodass

Dabei erhältst du folgendes lineare Gleichungssystem
(I) 
(II) 
(III) 
Erstelle zuerst die Matrix

und forme diese dann mithilfe des Gaußschen Eliminationsverfahrens in die Matrix

um. Damit erhältst du dann sofort die Werte
 ,
,  und
und 
Also lässt sich der Vektor  durch die folgende Linearkombination darstellen
durch die folgende Linearkombination darstellen



