Transponierte Matrix
Hier lernst du, was eine transponierte Matrix ist und wie du jede beliebige Matrix transponieren kannst. Du willst das Thema schnell verstehen? Dann schau dir unser Video an!
Inhaltsübersicht
Transponierte Matrix einfach erklärt
Eine transponierte Matrix erhältst du durch das Vertauschen von Zeilen und Spalten einer Matrix. So kannst du ganz einfach jede beliebige Matrix transponieren. Dabei wird die transponierte Matrix von  mit
mit  bezeichnet.
bezeichnet.
Betrachte die Matrix  , dann ist
, dann ist
 .
.
Die Zeile 1 von A wird zur Spalte 1 von  und die Zeile 2 von A zur Spalte 2 von
und die Zeile 2 von A zur Spalte 2 von  .
.
Beispiel 1
Betrachte folgende Matrix
 .
.
Die Matrix  transponierst du nun, indem du zunächst die erste Zeile als Spalte notierst.
transponierst du nun, indem du zunächst die erste Zeile als Spalte notierst.

Jetzt fehlt nur noch die zweite Zeile der ursprünglichen Matrix  , die du als zweite Spalte der transponierten Matrix
, die du als zweite Spalte der transponierten Matrix  ergänzt.
ergänzt.

Beispiel 2
Du kannst aber auch anders vorgehen und die Spalten in Zeilen umwandeln, um die transponierte Matrix zu berechnen.

Diesmal wird die Matrix  transponiert, indem du die erste Spalte als Zeile notierst.
transponiert, indem du die erste Spalte als Zeile notierst.

Genauso gehst du nun mit der zweiten und dritten Spalte vor.


Wie du siehst, kommst du über beide Wege zum selben Ergebnis. Es ist also egal, ob du aus Zeilen Spalten oder aus Spalten Zeilen machst.
Transponierte Matrix Rechenregeln
Nachdem du eine Matrix transponiert hast, kannst du natürlich noch weiter mit ihr rechnen. Die wichtigsten Regeln und Eigenschaften haben wir hier für dich zusammengefasst.

Bei der Addition spielt es keine Rolle, ob du die Matrizen erst zusammenrechnest und dann transponierst, oder ob du die transponierten Matrizen addierst.

Achtung bei der Multiplikation
von transponierten Matrizen! Hier werden  und
und  in umgekehrter Reihenfolge multipliziert.
in umgekehrter Reihenfolge multipliziert.

Viel unkomplizierter ist da die Skalarmultiplikation, hier kannst du das Multiplizieren und das Transponieren problemlos vertauschen.

Das doppelte Transponieren einer Matrix führt wieder zur ursprünglichen Matrix  .
.

Der Rang einer Matrix entspricht dem Rang der transponierten Matrix.

Auch die Spur einer Matrix verändert sich durch das Transponieren einer Matrix nicht.

Die Determinante einer Matrix entspricht der Determinante der transponierten Matrix.
Ist die Matrix invertierbar , so gilt:

Bei einer quadratischen Matrix kann es außerdem vorkommen, dass die ursprüngliche Matrix  und die transponierte Matrix
und die transponierte Matrix  gleich sind, also
gleich sind, also  gilt. In diesem Fall nennt man
gilt. In diesem Fall nennt man  symmetrische Matrix.
symmetrische Matrix.
Eine symmetrische Matrix erkennst du daran, dass die Einträge an der Hauptdiagonalen quasi gespiegelt sind:

Gilt  , dann wird die Matrix als antisymmetrisch oder schiefsymmetrisch bezeichnet.
, dann wird die Matrix als antisymmetrisch oder schiefsymmetrisch bezeichnet.
Transponierte Matrix Aufgabe
Im Folgenden haben wir dir noch zwei Aufgaben mit Lösungen zum Thema Matrizen transponieren zusammengestellt.
Aufgabe 1: 2×2 Matrix transponieren
Berechne die transponierte Matrix  .
.

Lösung Aufgabe 1
Durch das Vertauschen der Zeilen und Spalten bekommst du die transponierte Matrix:
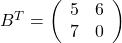
Aufgabe 2: 3×3 Matrix transponieren
Berechne die transponierte Matrix  .
.

Lösung Aufgabe 2
Das Vertauschen der Zeilen und Spalten führt zur transponierten Matrix:

Orthogonale Matrix
Gut gemacht! Jetzt weißt du genau, wie du eine Matrix transponierst. Mit der transponierten Matrix kannst du jetzt auch eine orthogonale Matrix bestimmen. Eine Matrix A ist orthogonal, wenn sie mit ihrer transponierten Matrix AT multipliziert, die Einheitsmatrix E ergibt.

Damit du in deiner Prüfung alle Aufgaben zu den Matrizen lösen kannst, musst du unbedingt wissen, wie du eine orthogonale Matrix bestimmst. Das erklären wir dir schnell und einfach in unserem Video dazu! Schau es dir gleich an!
