Lineare Gleichungssysteme
In diesem Beitrag erklären wir dir, was lineare Gleichungssysteme sind und wie du sie lösen kannst. Schau dir einfach unser Video dazu an! Darin erklären wir dir in kurzer Zeit alles, was du wissen musst.
Inhaltsübersicht
Was ist ein lineares Gleichungssystem?
Bei linearen Gleichungssystemen (kurz: LGS) hast du mehrere Gleichungen gegeben, in denen zwei oder mehr unbekannte Variablen vorkommen. Ein lineares Gleichungssystem mit 2 Unbekannten könnte zum Beispiel so aussehen:

Es besteht aus zwei Gleichungen, die jeweils zwei Variablen enthalten – in unserem Fall sind das  und
und  . Beim LGS lösen ist dein Ziel, Werte für die Variablen zu finden, sodass beide Gleichungen gleichzeitig erfüllt sind:
. Beim LGS lösen ist dein Ziel, Werte für die Variablen zu finden, sodass beide Gleichungen gleichzeitig erfüllt sind:

Es gibt mehrere Möglichkeiten, wie du lineare Gleichungssysteme lösen kannst:
- Gleichsetzungsverfahren (wenn beide Gleichungen nach der selben Variable aufgelöst sind)
- Einsetzungsverfahren (wenn eine Gleichung nach einer Variablen aufgelöst ist)
- Additionsverfahren (wenn zwei „entgegengesetzte Summanden“ vorkommen)
Du kannst jedes Verfahren verwenden, um das richtige Ergebnis zu bekommen. Je nach LGS bietet sich eines der drei besonders an, weil du damit am einfachsten rechnen kannst.
Wie du auf die Lösungen linearer Gleichungssysteme kommst, zeigen wir dir für alle Verfahren an ausführlichen Beispielen.
Lineare Gleichungssysteme Gleichsetzungsverfahren
Wenn beide Gleichungen in deinem linearen Gleichungssystem schon nach der selben Variable aufgelöst sind, wendest du das Gleichsetzungsverfahren an.
Das ist hier der Fall:

1. Gleichungen gleichsetzen: Beide Gleichungen sind nach  aufgelöst, also setzt du sie gleich.
aufgelöst, also setzt du sie gleich.

2. Nach Variable auflösen: Das musst du nach x auflösen.

So bekommst du als ersten Teil der Lösung  .
.
3. Andere Variable berechnen:  setzt du in
setzt du in  ein, um
ein, um  zu berechnen.
zu berechnen.

Das LGS wird also mit  gelöst.
gelöst.
4. Ergebnis überprüfen: Überprüfe dein Ergebnis, indem du beide Variablen in  einsetzt.
einsetzt.

5. Lösungsmenge aufstellen: Jetzt musst du die Lösungsmenge  formulieren. Die Lösung ist dabei ein Punkt mit den Koordinaten
formulieren. Die Lösung ist dabei ein Punkt mit den Koordinaten  und
und  — den schreibst du einfach hinter
— den schreibst du einfach hinter  in eine geschweifte Klammer.
in eine geschweifte Klammer.

Das kannst du auch graphisch darstellen:
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lineare Gleichungssysteme Einsetzungsverfahren
Wenn nur eine Gleichung nach einer Variablen aufgelöst ist, bietet sich das Einsetzungsverfahren an.
Das ist hier der Fall:

Gleichung  ist schon nach
ist schon nach  aufgelöst, also setzt du
aufgelöst, also setzt du  in
in  ein – daher auch Einsetzungsverfahren.
ein – daher auch Einsetzungsverfahren.
1. Term einer Variable in anderen Term einsetzen:

2. Nach Variable auflösen: Du musst den kombinierten Term nach  auflösen (y = …).
auflösen (y = …).

Du bekommst so heraus, dass  ist.
ist.
3. Andere Variable berechnen: Setze  in
in  , ein. So berechnest du
, ein. So berechnest du  .
.

Um das lineare Gleichungssystem berechnen, brauchst du  .
.
4. Ergebnis überprüfen: Setze beide Variablen in  ein.
ein.

5. Lösungsmenge aufstellen: Du weißt, dass  und
und  die Lösung für das lineare Gleichungssystem ist.
die Lösung für das lineare Gleichungssystem ist.
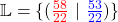
Lineare Gleichungssysteme Additionsverfahren
Wenn die Gleichungen „entgegengesetzte“ Terme enthalten, verwendest du das Additionsverfahren .
Das ist hier zum Beispiel der Fall, weil  in
in  und
und  in
in  enthalten sind.
enthalten sind.

Du rechnest  und
und  zusammen, um das lineare Gleichungssystem zu lösen – du führst eine Addition durch, deshalb auch Additionsverfahren.
zusammen, um das lineare Gleichungssystem zu lösen – du führst eine Addition durch, deshalb auch Additionsverfahren.
1. Gleichungen addieren: Du rechnest  . Alles, was links vom
. Alles, was links vom  steht, schreibst du links und alles, was rechts steht, rechts.
steht, schreibst du links und alles, was rechts steht, rechts.

2. Nach Variable auflösen: Die entgegengesetzten Terme  und
und  heben sich auf, also bleibt als Variable nur
heben sich auf, also bleibt als Variable nur  . Danach löst du auf.
. Danach löst du auf.

3. Andere Variable berechnen: Setze  in
in  ein, um
ein, um  zu berechnen.
zu berechnen.

4. Ergebnis überprüfen: Setze beide Variablen in  ein.
ein.

5. Lösungsmenge aufstellen: Bilde die Lösungsmenge für das LGS.

Jetzt kennst du also drei Verfahren, mit denen du lineare Gleichungssysteme lösen kannst. Super!
In manchen Fällen kann es sein, dass du eine Gleichung erst umformen musst, bevor du eines der Verfahren anwenden kannst. Wie das geht, siehst du in unserem Beitrag Lineare Gleichungssysteme Aufgaben .
Gleichungssysteme lösen – Besonderheiten
Es könnte auch passieren, dass dir zwei Spezialfälle beim Lösen von linearen Gleichungssystemen begegnen. Ein lineares Gleichungssystem kann nämlich gar keine oder unendlich viele Lösungen haben. Schauen wir uns dazu je ein Beispiel an.
Keine Lösung:

Du siehst, dass  schon ganz nach
schon ganz nach  aufgelöst ist, also verwendest du das Einsetzungsverfahren und setzt
aufgelöst ist, also verwendest du das Einsetzungsverfahren und setzt  aus
aus  in
in  ein.
ein.
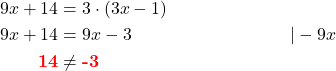
Hier würde am Ende  stehen. Aber das ist natürlich nie richtig! Das heißt, es gibt keine Lösung für dieses lineare Gleichungssystem. Du schreibst die Lösungsmenge trotzdem hin, aber sie bleibt leer.
stehen. Aber das ist natürlich nie richtig! Das heißt, es gibt keine Lösung für dieses lineare Gleichungssystem. Du schreibst die Lösungsmenge trotzdem hin, aber sie bleibt leer.

Unendlich viele Lösungen:

Du setzt  in
in  ein, um das LGS zu lösen.
ein, um das LGS zu lösen.

Dass  ist, gilt immer – egal welche Zahlen du für
ist, gilt immer – egal welche Zahlen du für  und
und  einsetzt. Das heißt, das lineare Gleichungssystem hat unendlich viele Lösungen. Die Lösungsmenge schreibst du dann als alle Zahlen
einsetzt. Das heißt, das lineare Gleichungssystem hat unendlich viele Lösungen. Die Lösungsmenge schreibst du dann als alle Zahlen  und
und  , für die
, für die  gilt.
gilt.

Lineare Gleichungssysteme Aufgaben
Das Beste bei so einem schweren Thema ist es, wenn du selbst etwas durchrechnest. Schau dir deshalb unbedingt auch noch unser Video zum Thema Lineare Gleichungssysteme Aufgaben an! Da zeigen wir dir, wie lineare Gleichungssysteme noch aussehen könnten und erklären dir nochmal genau, wie du auf die Lösungen kommst.
Lineare Gleichungssysteme mit drei Variablen
Ein lineares Gleichungssystem mit 2 Variablen nennst du ein  -System — dabei hast du 2 Geradengleichungen und 2 Unbekannte. Es gibt aber auch lineare Gleichungssysteme mit mehr als zwei Variablen. Ein lineares Gleichungssystem mit 3 Variablen nennst du dann ein
-System — dabei hast du 2 Geradengleichungen und 2 Unbekannte. Es gibt aber auch lineare Gleichungssysteme mit mehr als zwei Variablen. Ein lineares Gleichungssystem mit 3 Variablen nennst du dann ein  -Gleichungssystem. Schauen wir uns mal ein Beispiel für so ein System an, das aus drei Gleichungen mit 3 Unbekannten besteht.
-Gleichungssystem. Schauen wir uns mal ein Beispiel für so ein System an, das aus drei Gleichungen mit 3 Unbekannten besteht.

Du löst es, indem du schrittweise die Variablen eliminierst.
1. Erste Variable eliminieren: Wenn du genau hinsiehst, entdeckst du, dass  und
und  jeweils
jeweils  und
und  enthalten. Deswegen wendest du auf
enthalten. Deswegen wendest du auf  und
und  das Additionsverfahren an und rechnest sie zusammen, um
das Additionsverfahren an und rechnest sie zusammen, um  loszuwerden.
loszuwerden.

 schreibst du anstelle von
schreibst du anstelle von  in das LGS.
in das LGS.
2. Zweite Variable eliminieren: Jetzt musst du auch  und
und  so addieren, dass
so addieren, dass  wegfällt. Davor musst du eine Multiplikation durchführen, damit sich die Vorfaktoren von
wegfällt. Davor musst du eine Multiplikation durchführen, damit sich die Vorfaktoren von  gleichen. Hier multiplizierst du
gleichen. Hier multiplizierst du  mit -0,25. Dann heben sich die
mit -0,25. Dann heben sich die  aus
aus  und
und  auf.
auf.

Du addierst  und
und  , damit sich
, damit sich  und
und  aufheben.
aufheben.

 schreibst du statt
schreibst du statt  in das lineare Gleichungssystem.
in das lineare Gleichungssystem.
3. Terme kombinieren: und
und  enthalten beide nur
enthalten beide nur  und
und  . Löse jetzt
. Löse jetzt  nach
nach  auf und setze
auf und setze  in
in  ein, um einen Zahlenwert für
ein, um einen Zahlenwert für  zu erhalten.
zu erhalten.

 in
in  :
:

4. Einen Zahlenwert einsetzen: So weißt du, dass  ist und setzt das in
ist und setzt das in  ein, um auch einen Zahlenwert für
ein, um auch einen Zahlenwert für  zu bekommen.
zu bekommen.

5. Beide Zahlenwerte einsetzen: Um  zu erhalten setzt du
zu erhalten setzt du  und
und  in
in  ein.
ein.

6. Ergebnis überprüfen: Du siehst so, dass  ist. Wenn du dir unsicher bist, ob du das LGS mit 3 Unbekannten richtig gelöst hast, setzt du deine Ergebnisse in eine der drei Gleichungen, hier
ist. Wenn du dir unsicher bist, ob du das LGS mit 3 Unbekannten richtig gelöst hast, setzt du deine Ergebnisse in eine der drei Gleichungen, hier  , ein.
, ein.


7. Lösungsmenge aufstellen: Zuletzt schreibst du die Lösungsmenge hin.

Gauß-Algorithmus
Es gibt noch eine weitere Möglichkeit, wie du lineare Gleichungssysteme lösen kannst — den Gauß-Algorithmus. Zu dem Thema haben wir auch ein Video für dich vorbereitet. Schau es dir jetzt unbedingt noch an! Dann weißt du wirklich ganz genau, wie du lineare Gleichungssysteme lösen kannst.





