Eigenwert
In diesem Artikel erfährst du, was ein Eigenwert eigentlich ist und wie man Eigenwerte Schritt für Schritt berechnen kann. An zwei Beispielen wenden wir die Berechnung dann dann praktisch an und zeigen dir, auf was du achten musst!
Noch einprägsamer lässt sich das alles in einem Video vermitteln, das wir zu dem Thema für dich erstellt haben.
Inhaltsübersicht
Eigenwerte einfach erklärt
Die Multiplikation einer Matrix mit einem Vektor ergibt wieder einen Vektor. Für quadratische Matrizen gibt es bestimmte Vektoren, die man an die Matrix multiplizieren kann, sodass man den selben Vektor als Ergebnis erhält, nur mit einem Vorfaktor multipliziert. Einen solchen Vektor nennt man Eigenvektor und der Vorfaktor heißt Eigenwert einer Matrix.
Eigenwerte und Eigenvektoren
Hat man eine Lösung gefunden, so nennt man die reelle oder komplexe Zahl  einen Eigenwert der Matrix. Der Vektor
einen Eigenwert der Matrix. Der Vektor  heißt dann Eigenvektor. Dieser darf nach der Definition nicht der Nullvektor sein. Die Menge der Eigenwerte einer Matrix wird als Spektrum der Matrix bezeichnet.
heißt dann Eigenvektor. Dieser darf nach der Definition nicht der Nullvektor sein. Die Menge der Eigenwerte einer Matrix wird als Spektrum der Matrix bezeichnet.
Algorithmus
Es sei die  -Matrix
-Matrix  vorgegeben und zu dieser wollen wir die Eigenwerte berechnen. Folgende Schritte musst du dabei durchführen.
vorgegeben und zu dieser wollen wir die Eigenwerte berechnen. Folgende Schritte musst du dabei durchführen.
- Bilde die Matrix
 .
.  steht für die Einheitsmatrix. Du musst also in der Matrix
steht für die Einheitsmatrix. Du musst also in der Matrix  auf der Diagonalen immer den Wert
auf der Diagonalen immer den Wert  abziehen.
abziehen. - Berechne die Determinante dieser Matrix. Diese nennt man das charakteristische Polynom
 der Matrix
der Matrix  . Es ist ein Ausdruck in Abhängigkeit von
. Es ist ein Ausdruck in Abhängigkeit von  .
. - Bestimme die Nullstellen des charakteristischen Polynoms
 . Das sind genau die gesuchten Eigenwerte der Matrix.
. Das sind genau die gesuchten Eigenwerte der Matrix.
Herleitung
Nun wollen wir zeigen, wie man zu dieser Berechnungsvorschrift gelangt. Dazu betrachten wir erst einmal das Eigenwertproblem, das es zu lösen gilt:

Diese Gleichung lässt sich mithilfe der Einheitsmatrix  umformulieren:
umformulieren:


Gibt es nun eine Zahl  und einen Vektor
und einen Vektor  , sodass dieser durch Multiplikation mit der Matrix
, sodass dieser durch Multiplikation mit der Matrix  auf den Nullvektor abgebildet wird, so ist diese Matrix nicht von vollem Rang und die Multiplikation mit einem Vektor nicht injektiv
. Dass die Matrix
auf den Nullvektor abgebildet wird, so ist diese Matrix nicht von vollem Rang und die Multiplikation mit einem Vektor nicht injektiv
. Dass die Matrix  keinen vollen Rang besitzt ist gleichbedeutend damit, dass ihre Determinante Null ist. Wenn es also eine Lösung des Eigenwertproblems gibt, muss gelten:
keinen vollen Rang besitzt ist gleichbedeutend damit, dass ihre Determinante Null ist. Wenn es also eine Lösung des Eigenwertproblems gibt, muss gelten:

Um das Eigenwertproblem zu lösen, müssen also die Nullstellen des charakteristischen Polynoms

ermittelt werden, genau wie es der Algorithmus vorschreibt.
Beispiel: Eigenwert 3×3-Matrix
Nun wollen wir für eine 3×3-Matrix die Eigenwerte bestimmen. Dazu betrachten wir die folgende Matrix:

Wir wollen im Folgenden die drei Schritte des Algorithmus einzeln abarbeiten.
Zunächst berechnen wir dazu die Matrix  :
:

Anschließend ermitteln wir deren Determinante:

Im letzten Schritt müssen wir die Nullstellen dieses Polynoms bestimmen. Durch Ausprobieren erhalten wir schnell die erste Nullstelle  . Klammern wir dann den Faktor
. Klammern wir dann den Faktor  aus, erhalten wir:
aus, erhalten wir:
 .
.
Die restlichen Nullstellen sind also Nullstellen des Polynoms  . Diese lassen sich mithilfe der Mitternachtsformel bestimmen:
. Diese lassen sich mithilfe der Mitternachtsformel bestimmen:

Somit lauten die drei Eigenwerte der 3×3-Matrix  .
.
Beispiel: Eigenwert symmetrische Matrix
In diesem Beispiel soll die symmetrische Matrix

betrachtet werden. Auch hier wollen wir die Eigenwerte bestimmen.
Im ersten Schritt berechnen wir also wieder die Matrix  :
:

Nun bestimmen wir ihre Determinante:

Der letzte Schritt besteht nun darin, die Nullstellen dieses Polynoms zu bestimmen. In der dargestellten Form des Polynoms lassen sich diese einfach ablesen. Die Eigenwerte der Matrix sind also  .
.
Eigenschaften
Will man Eigenwerte berechnen, so ist es häufig nützlich, wenn man ein paar Eigenschaften darüber kennt. Daher sollen im Folgenden ein paar derer aufgezählt werden.
- Sei
 ein Eigenwert der invertierbaren Matrix
ein Eigenwert der invertierbaren Matrix  mit dem Eigenvektor
mit dem Eigenvektor  . Dann ist auch
. Dann ist auch  ein Eigenwert der inversen Matrix von
ein Eigenwert der inversen Matrix von  zum Eigenvektor
zum Eigenvektor  .
. - Seien
 die Eigenwerte der Matrix
die Eigenwerte der Matrix  . Dann gilt:
. Dann gilt:
-
- Ist
 ein Eigenwert einer Matrix
ein Eigenwert einer Matrix  , so ist er auch ein Eigenwert der transponierten Matrix
, so ist er auch ein Eigenwert der transponierten Matrix  und umgekehrt. Das Spektrum von
und umgekehrt. Das Spektrum von  stimmt also mit dem Spektrum der Transponierten
stimmt also mit dem Spektrum der Transponierten  überein.
überein. - Jeder Eigenwert einer reellen symmetrischen Matrix ist reell. Im Allgemeinen können aber auch komplexe Eigenwerte durchaus auftreten.
Mit Kenntnis dieser Eigenschaften lassen sich häufig Eigenwerte bestimmen, ohne dabei viel rechnen zu müssen.
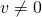 und einer Zahl
und einer Zahl 
![Rendered by QuickLaTeX.com \[\sum_{i=1}^n \lambda_i=\mathrm{Spur}(A)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-13a2e82881832088e7b7733c1642e6df_l3.png)
![Rendered by QuickLaTeX.com \[\prod_{i=1}^n\lambda_i=\mathrm{det}(A)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f80dd5cbee57125d5cd8e38e78ff5e94_l3.png)