Wurzel ableiten
In diesem Artikel erfährst du, wie du die Wurzel ableiten kannst. Dabei gehen wir auf die Kettenregel ein und zeigen dir viele Beispiele, in denen wir Wurzeln ableiten. Wenn du in kürzester Zeit alles Wichtige zum Ableiten von Wurzel x erfahren möchtest, schau dir unser Video an.
Inhaltsübersicht
Wurzel ableiten einfach erklärt
Die Ableitung von Wurzel x kannst du dir ganz einfach merken:
![Rendered by QuickLaTeX.com \[f(x) = \sqrt{\textcolor{blue}{x}} \qquad \underrightarrow{abgeleitet} \qquad f'(x) = \frac{1}{2\sqrt{\textcolor{blue}{x}}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ff9b35ee0fc1d79ff10c285e055bf06d_l3.png)
Etwas schwieriger wird es, wenn unter der Wurzel nicht nur ein x steht, sondern eine andere Funktion. Dann brauchst du zum Ableiten die Kettenregel .
Schau dir dazu das Beispiel  an. Die Funktion unter der Wurzel ist hier 2x. Die Ableitung davon ergibt 2. Deshalb ist die gesamte Ableitung der Wurzel:
an. Die Funktion unter der Wurzel ist hier 2x. Die Ableitung davon ergibt 2. Deshalb ist die gesamte Ableitung der Wurzel:
![Rendered by QuickLaTeX.com \[f(x) = \sqrt{\textcolor{blue}{2x}} \qquad \underrightarrow{abgeleitet} \qquad f'(x) = \frac{1}{2\sqrt{\textcolor{blue}{2x}}} \cdot \textcolor{red}{2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0e4ba8087a91fb98eaa75191bd362820_l3.png)
Allgemein kannst du dir merken:
![Rendered by QuickLaTeX.com \[f(x) = \sqrt{\textcolor{blue}{\text{Funktion}}} \qquad \underrightarrow{abgeleitet} \qquad f'(x) = \frac{1}{2\sqrt{\textcolor{blue}{\text{Funktion}}}} \cdot \textcolor{red}{\text{Ableitung der Funktion}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a6d0b18bc17f3a925998a7caaa5b302c_l3.png)
Beispiel 1 — Kettenregel
Schau dir gleich noch weitere Beispiele an, wie du bei komplizierteren Wurzelfunktionen die Ableitung bestimmen kannst. Du brauchst dafür immer die Kettenregel.
Bestimme die Ableitung der Funktion
![Rendered by QuickLaTeX.com \[f(x)=\sqrt{\textcolor{blue}{2x^2+1}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-64a09204b3e94d482dbdade727c3883a_l3.png)
Dafür gehst du so vor:
-
Schritt 1: Bestimme die Ableitung der Funktion in der Wurzel
. Dafür verwendest du die Potenzregel
. Die Funktion in der Wurzel nennst du dafür g(x).
![Rendered by QuickLaTeX.com \[g(x) = \textcolor{blue}{2x^2+1} \qquad \underrightarrow{abgeleitet} \qquad g'(x) = \textcolor{red}{4x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c797c62cdece1790df017b7ce45a22e2_l3.png)
-
Schritt 2: Berechne die gesamte Ableitung der Wurzel.
![Rendered by QuickLaTeX.com \[f'(x) = \frac{1}{2\sqrt{\textcolor{blue}{g(x)}}}\cdot \textcolor{red}{g'(x)}=\frac{1}{2\sqrt{\textcolor{blue}{2x^2+1}}}\cdot \textcolor{red}{4x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-91f6dd997f76c34893a7b73d618fd857_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 2 — Dritte Wurzel
Schau dir noch ein weiteres Beispiel für die Ableitung einer Wurzel an:
![Rendered by QuickLaTeX.com \[f(x)=\sqrt[3]{6x-2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-120499b0fa66a98fe93032c9faecd0f4_l3.png)
Du siehst, dass es hier nicht mehr um eine Quadratwurzel geht, sondern um die 3. Wurzel. Um die ableiten zu können, musst du sie als Erstes umschreiben:
![Rendered by QuickLaTeX.com \[f(x)=\sqrt[\textcolor{teal}{3}]{6x-2} = \left(6x-2\right)^{\frac{1}{\textcolor{teal}{3}}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-bd033ecc8542f8017a7ad81051c1bf61_l3.png)
Jetzt betrachtest du für die Kettenregel:
- wie gewohnt g(x) = 6x – 2
- die äußere Funktion
![Rendered by QuickLaTeX.com h(y) = \sqrt[\textcolor{teal}{3}]{y} = y^{\frac{1}{\textcolor{teal}{3}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-169c67c6d4e51b46a0d13a172dfd5303_l3.png) . Anstatt 6x -2 schreibst du also einfach erstmal ein y in die Wurzel.
. Anstatt 6x -2 schreibst du also einfach erstmal ein y in die Wurzel.
Dann gehst du so vor:
- Schritt 1: Bestimme die Ableitung von g(x): g'(x) = 6
-
Schritt 2: Bestimme die Ableitung von h(y). Das kannst du wie gewohnt mit der Potenzregel machen:
![Rendered by QuickLaTeX.com \[h'(y) = \frac{1}{\textcolor{teal}{3}} \cdot y^{\frac{1}{\textcolor{teal}{3}}-1} = \frac{1}{\textcolor{teal}{3}} \cdot y^{-\frac{2}{3}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-90c6468b917c9ac80db53222e8124f45_l3.png)
-
Schritt 3: Setze g und h mit der Kettenregel zusammen.
![Rendered by QuickLaTeX.com \[f'(x) = h'(\textcolor{blue}{g(x)}) \cdot \textcolor{red}{g'(x)} = \frac{1}{\textcolor{teal}{3}} \cdot (\textcolor{blue}{6x-2})^{-\frac{2}{3}} \cdot \textcolor{red}{6}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2d117b46a8b0c678f25511cd5059bba7_l3.png)
Schon gewusst? Du kannst ![Rendered by QuickLaTeX.com \sqrt[3]{y}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f49d30da611c50f896a33adcc11753c7_l3.png) ,
, ![Rendered by QuickLaTeX.com \sqrt[4]{y}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-23c254ce684e37c14e518ff9bed0ae1d_l3.png) ,
, ![Rendered by QuickLaTeX.com \sqrt[5]{y}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d9ed4edc196b5ac925c8233531a4b7fd_l3.png) , … auch mit einer Formel ableiten. Allgemein gilt für die n-te Wurzel:
, … auch mit einer Formel ableiten. Allgemein gilt für die n-te Wurzel:
![Rendered by QuickLaTeX.com \[(\sqrt[n]{y})' =\frac{1}{n} \cdot y^{\frac{1-n}{n}} = \frac{1}{n\cdot \sqrt[n]{y^{n-1}}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2daf75f843f7fe1ce6c59535684b2e07_l3.png)
Ableitung Wurzel
Bisher haben wir beim Wurzel Ableiten neben der Kettenregel nur die Potenz- und die Faktorregel angewandt. Bei den folgenden Beispielen musst du, um die Funktion mit der Wurzel ableiten zu können, noch weitere Ableitungsregeln anwenden.
| Ableitungsregel | Funktion | Ableitung |
| Summenregel |

|

|
| Differenzregel |

|

|
| Produktregel |

|

|
| Quotientenregel |

|
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png)
|
| Faktorregel |
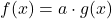
|

|
| Potenzregel |

|
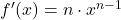
|
Wurzel ableiten — häufigste Fragen
(ausklappen)
Wurzel ableiten — häufigste Fragen
(ausklappen)-
Wie erkenne ich schnell, was bei einer Wurzelfunktion die innere Funktion g(x) ist?g(x) ist immer genau der gesamte Ausdruck, der unter dem Wurzelzeichen steht. Die Wurzel selbst ist die äußere Funktion, also
 . Beispiel: Bei
. Beispiel: Bei  gilt
gilt  .
.
-
Welche Fehler passieren am häufigsten, wenn ich die Kettenregel bei √(g(x)) anwende?Am häufigsten wird der Faktor g'(x) vergessen oder die innere Ableitung falsch gebildet. Außerdem wird oft fälschlich
 statt
statt  geschrieben. Beispiel:
geschrieben. Beispiel:  .
.
-
Wie leite ich eine Funktion wie 1/√(g(x)) ab, ohne mich beim Umformen zu vertun?Schreibe
 als Potenz
als Potenz ![Rendered by QuickLaTeX.com [g(x)]^{-\frac{1}{2}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-e12c9b6c72f8dc8d610d3492fac92f18_l3.png) und nutze dann Ketten- und Potenzregel. So bleibt die Struktur klar:
und nutze dann Ketten- und Potenzregel. So bleibt die Struktur klar: ![Rendered by QuickLaTeX.com f'(x)=-\frac{1}{2}\cdot [g(x)]^{-\frac{3}{2}}\cdot g'(x)](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-fdc80546346cca81f5b9f7e113174c52_l3.png) . Beispiel: Für
. Beispiel: Für  ist
ist  .
.
-
Wann darf ich eine Wurzel zu einer Potenz umschreiben, ohne den Definitionsbereich zu verändern?Bei geraden Wurzeln darfst du
 zu
zu ![Rendered by QuickLaTeX.com [g(x)]^{\frac{1}{2}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-4c0918d2981a7c6910bf2bb04e6d4608_l3.png) umschreiben, wenn du im Reellen bleibst und weiterhin
umschreiben, wenn du im Reellen bleibst und weiterhin  verlangst. Bei ungeraden Wurzeln wie
verlangst. Bei ungeraden Wurzeln wie ![Rendered by QuickLaTeX.com \sqrt[3]{g(x)}=[g(x)]^{\frac{1}{3}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-16edf1be9922aa010bb4fa69650c74be_l3.png) gibt es keine solche Einschränkung.
gibt es keine solche Einschränkung.
Weitere Funktionen und ihre Ableitungen
Die Ableitungen der folgenden Funktionen solltest du ebenfalls kennen und anwenden können.
| Funktion | Ableitung | |
| e Funktion ableiten |  |
 |
| Ableitung Cosinus |  |
 |
| Ableitung Sinus |  |
 |
| Ableitung Tangens |  |
 |
| ln ableiten | 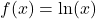 |
 |











