Komplexe Zahlen
In diesem Beitrag zeigen wir dir unter anderem was komplexe Zahlen sind und wie du mit ihnen rechnest. In unserem Video lernst du das Wichtigste zu komplexen Zahlen in kurzer Zeit.
Inhaltsübersicht
Was sind komplexe Zahlen?
Nehmen wir an, dass du die folgende Gleichung lösen möchtest
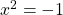 .
.
Mit den dir bisher bekannten reellen Zahlen, findest du dafür keine Lösung, denn das Quadrat jeder reellen Zahl ist nicht-negativ. Und genau hier kommen die komplexen Zahlen ins Spiel.
Dazu wurde die 
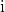 eingeführt, die gerade diese Eigenschaft hat, dass ihr Quadrat eine negative Zahl ist
eingeführt, die gerade diese Eigenschaft hat, dass ihr Quadrat eine negative Zahl ist
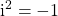 .
.
Komplexe Zahlen sind dann eine bestimmte Kombination aus zwei reellen Zahlen, die 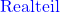 und
und  heißen. Diese Kombination sieht so aus
heißen. Diese Kombination sieht so aus
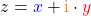 .
.
Das heißt, die komplexe Zahl  würde die Gleichung am Anfang lösen.
würde die Gleichung am Anfang lösen.
Komplexe Zahlen Beispiele
Beispiele für komplexe Zahlen sind
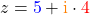 ,
,
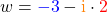 oder
oder
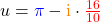
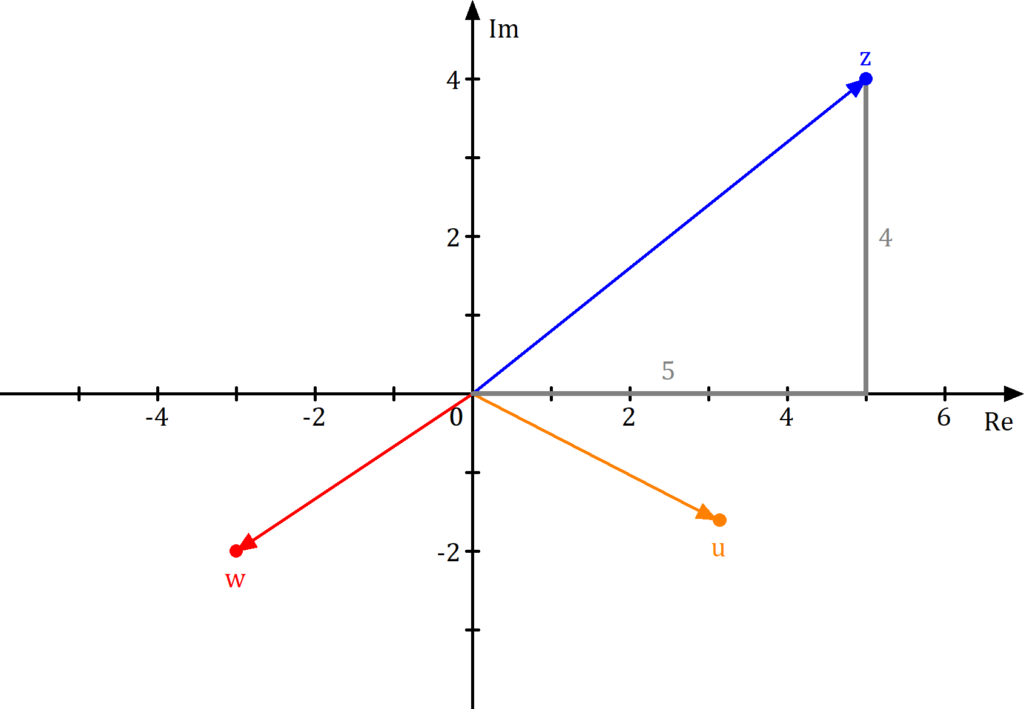
Du kannst dir komplexe Zahlen als Punkte oder Vektoren
in einem Koordinatensystem vorstellen. Die komplexe Zahl  zum Beispiel hat als Re(z) =
zum Beispiel hat als Re(z) = 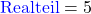 und als Im(z) =
und als Im(z) =  .
.
Dieses Koordinatensystem bekommt den besonderen Namen komplexe Zahlenebene oder Gaußsche Zahlenebene .
Komplexe Zahlen Rechenregeln Übersicht
Hier eine Übersicht wichtiger Rechenregeln. Im folgenden werden wir auf diese Rechenregeln nicht nur näher eingehen, sondern dir auch Beispiele zeigen.
|
Komplexe Zahlen Struktur |
|
|
Realteil Re und Imaginärteil Im |
Re(z) = a , Im(z) = b ; Re(w) = c , Im(w) = d |
|
Addition und Subtraktion |
|
|
Multiplikation |
|
|
Division |
|
|
Komplex konjugiert |
Vorzeichen von Im wechseln: |
| Betrag | Abstand vom Ursprung: 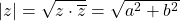
|
Komplexe Zahlen Rechenregeln
In diesem Abschnitt erklären wir dir, wie du komplexe Zahlen addierst, subtrahierst, multiplizierst und dividierst. Am Ende dieses Abschnittes zeigen wir dir auch, wie du den Betrag einer komplexen Zahl berechnest.
Komplexe Zahlen addieren und subtrahieren
Sagen wir, du hast zwei komplexe Zahlen gegeben
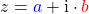 und
und  .
.
Wenn du diese addieren möchtest, dann rechnest du
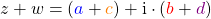
und wenn du sie subtrahieren möchtest
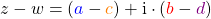 .
.
Beispiel
Nehmen wir an, dass du die folgenden komplexen Zahlen gegeben hast
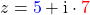 und
und 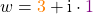 .
.
Wenn du  und
und 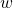 addierst, dann bekommst du
addierst, dann bekommst du
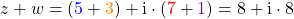 .
.
Ziehst du hingegen von  die komplexe Zahl
die komplexe Zahl 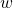 ab, dann erhältst du
ab, dann erhältst du
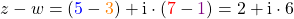 .
.
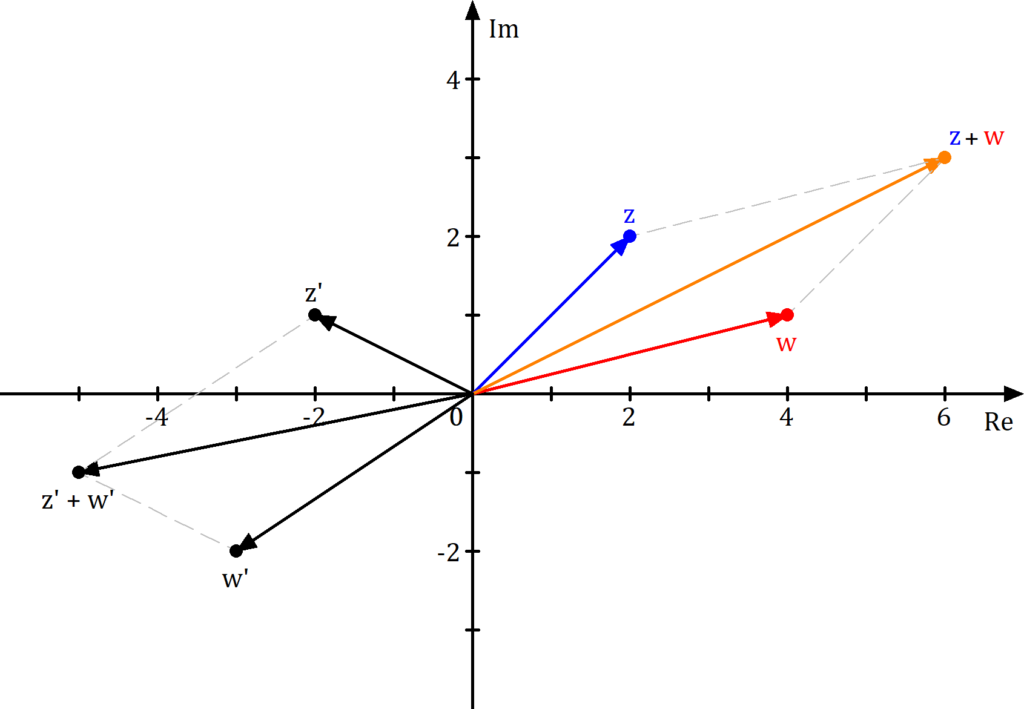
In der Gaußschen Zahlenebene kannst du dir die Addition (und Subtraktion) von komplexen Zahlen wie die Vektoraddition vorstellen. Das heißt, du bildest mit den beiden „Vektoren“  und
und 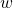 (beziehungsweise
(beziehungsweise 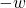 ) ein Parallelogramm. Die Diagonale ist dann das Ergebnis der Addition (oder Subtraktion).
) ein Parallelogramm. Die Diagonale ist dann das Ergebnis der Addition (oder Subtraktion).
Beispiel
Wir nehmen die komplexen Zahlen aus dem vorherigen Beispiel
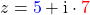 und
und 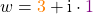 .
.
Multiplizierst du jetzt  und
und 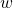 miteinander, dann erhältst du
miteinander, dann erhältst du
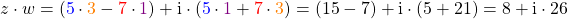 .
.
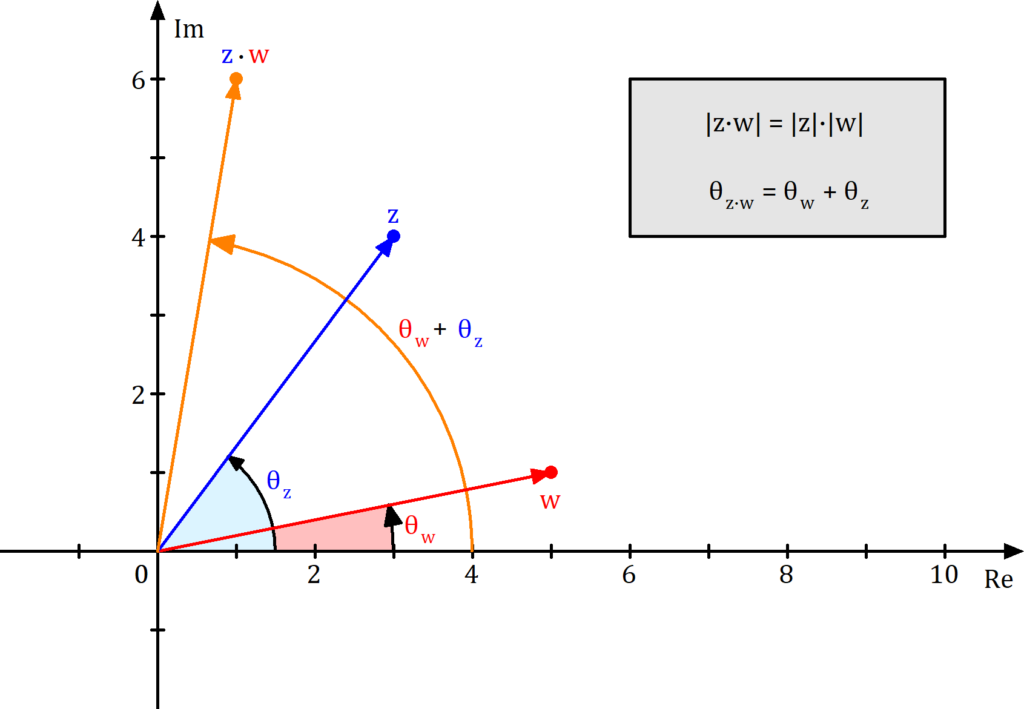
Auch die Multiplikation kannst du dir in der Gaußschen Zahlenebene veranschaulichen. Wenn du das Produkt 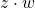 berechnest, dann nimmst du den „Vektor“
berechnest, dann nimmst du den „Vektor“  , skalierst seine Länge um die Länge von dem „Vektor“
, skalierst seine Länge um die Länge von dem „Vektor“ 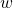 , also
, also 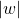 , und rotierst ihn zusätzlich um den Winkel vom „Vektor“
, und rotierst ihn zusätzlich um den Winkel vom „Vektor“ 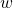 , also
, also 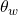 .
.
Merke: Die Multiplikation in der Gaußschen Zahlenebene entspricht dem Strecken oder Stauchen mit zusätzlicher Rotation eines Vektors.
Hinweis: Du musst diese Formel nicht auswendig lernen. Du kannst sie herleiten. Dafür brauchst du nur das Ausmultiplizieren von Klammern. Dabei musst du darauf achten, dass 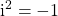 gilt. Das funktioniert folgendermaßen
gilt. Das funktioniert folgendermaßen
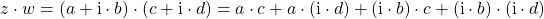
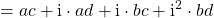
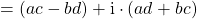 .
.
Komplex konjugiert
Was hat es mit diesem Strich über 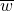 auf sich? Das ist die zu
auf sich? Das ist die zu 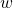 komplexe konjugierte Zahl. Schauen wir uns das genauer an und nehmen dafür die komplexe Zahl
komplexe konjugierte Zahl. Schauen wir uns das genauer an und nehmen dafür die komplexe Zahl  her
her
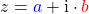 .
.
Wenn du jetzt das Vorzeichen des Imaginärteils Im(z)  umkehrst, erhältst du die zu
umkehrst, erhältst du die zu  komplex konjugierte Zahl
komplex konjugierte Zahl 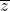
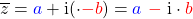 .
.
Mehr zu komplex konjugiert findest du in unserem Beitrag hier .
Beispiel
Die komplexen Zahlen für das Beispiel lauten wieder
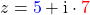 und
und 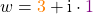 .
.
Schritt 1: Im ersten Schritt berechnen wir 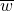 . Das heißt, wir kehren das Vorzeichen von
. Das heißt, wir kehren das Vorzeichen von  um. Dadurch erhalten wir
um. Dadurch erhalten wir
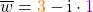 .
.
Schritt 2: Jetzt berechnen wir das Produkt 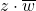
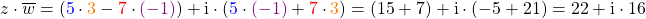 .
.
Schritt 3: Nun berechnen wir das Produkt 
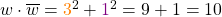 .
.
Schritt 4: Wir haben alle Zutaten zusammen und müssen diese nur noch in die Formel einfügen
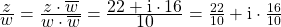 .
.
Merke: Dieser Prozess den Zähler und Nenner mit 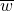 zu multiplizieren, heißt komplex konjugiert erweitern. Wenn du eine komplexe Zahl
zu multiplizieren, heißt komplex konjugiert erweitern. Wenn du eine komplexe Zahl  mit der dazu komplex konjugierten Zahl
mit der dazu komplex konjugierten Zahl 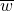 multiplizierst, dann erhältst du als Ergebnis immer
multiplizierst, dann erhältst du als Ergebnis immer
 PLUS
PLUS  .
.
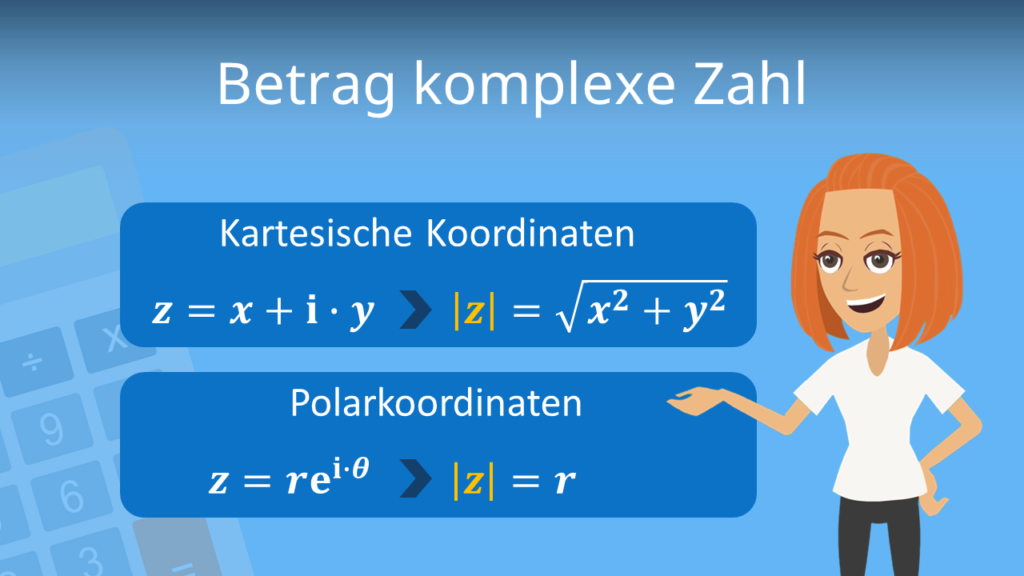
Betrag komplexe Zahl
Zum Schluss schauen wir uns noch an, wie du den Betrag einer komplexen Zahl berechnest. Dazu nehmen wir uns die komplexe Zahl  her
her 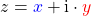 .
.
Möchtest du den Betrag von  bestimmen, dann rechnest du
bestimmen, dann rechnest du
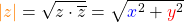 .
.
Hinweis: Wenn du dir die komplexe Zahl  als Punkt in der Zahlenebene vorstellst, dann entspricht der Betrag gerade dem Abstand vom Ursprung
. Mehr dazu findest du in unserem Beitrag hier
.
als Punkt in der Zahlenebene vorstellst, dann entspricht der Betrag gerade dem Abstand vom Ursprung
. Mehr dazu findest du in unserem Beitrag hier
.
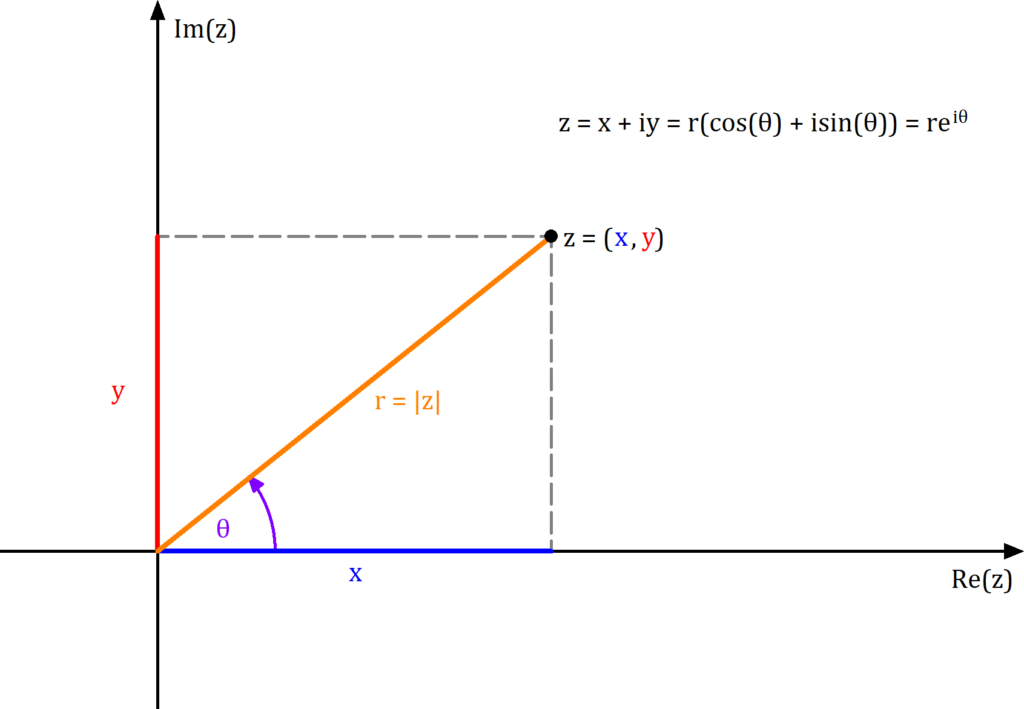
Komplexe Zahlen Polarform
Bisher haben wir uns komplexen Zahlen in ihrer kartesischen Darstellung angeschaut. Du kannst stattdessen aber auch Polarkoordinaten verwenden. Das bedeutet, dass du eine komplexe Zahl  dadurch bestimmst, indem du den Abstand
dadurch bestimmst, indem du den Abstand  vom Ursprung und den Winkel
vom Ursprung und den Winkel  zur
zur 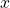 -Achse angibst. Dieser Winkel heißt auch
-Achse angibst. Dieser Winkel heißt auch  .
.
Verwendest du Polarkoordinaten, dann sieht eine komplexe Zahl  so aus
so aus
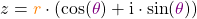 ,
,
wenn du sie mit Sinus und Cosinus ausdrückst. Du kannst aber auch die e-Funktion verwenden. Die komplexe Zahl in der Exponentialform sieht dann so aus
 .
.
Ein Beispiel dafür ist
 .
.
Kartesische Koordinaten auf Polarkoordinaten
Du hast die komplexe Zahl  in kartesischen Koordinaten gegeben
in kartesischen Koordinaten gegeben
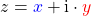 .
.
Um den Abstand  zu bestimmen, berechnest du den Betrag von
zu bestimmen, berechnest du den Betrag von 
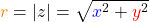 .
.
Möchtest du nun auch das Argument  berechnen, dann musst du vier Fälle unterscheiden:
berechnen, dann musst du vier Fälle unterscheiden:
- Wenn
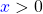 und
und 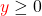 sind, dann rechnest du
sind, dann rechnest du 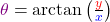 ;
; - Ist hingegen
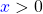 und
und 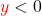 , dann rechnest du
, dann rechnest du 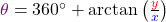 .
. - Und falls
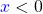 ist, dann rechnest du
ist, dann rechnest du 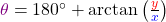 .
. - Wenn
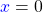 ist, kommt es nur auf y an. Ist
ist, kommt es nur auf y an. Ist 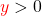 , dann ist
, dann ist 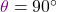 . Sonst ist für
. Sonst ist für 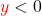 der Winkel
der Winkel 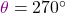 .
.
Beispiel
Nehmen wir an, dass du die folgende komplexe Zahl in kartesischer Darstellung gegeben hast
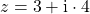 .
.
Du möchtest davon die Darstellung in Polarkoordinaten berechnen.
Für das Argument 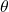 musst du zunächst überprüfen, welche der vier Fälle vorliegen. Hier sind Real- und Imaginärteil größer als Null. Du rechnest daher
musst du zunächst überprüfen, welche der vier Fälle vorliegen. Hier sind Real- und Imaginärteil größer als Null. Du rechnest daher
![Rendered by QuickLaTeX.com \[\textcolor{violet}{\theta} = \arctan \left(\frac{\textcolor{red}{y}}{\textcolor{blue}{x}}} \right ) = \arctan \left(\frac{\textcolor{red}{4}}{\textcolor{blue}{3}} \right ) \approx 53^{\circ} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cd9da3901d5c667cc89400281235c8d8_l3.png)
Jetzt rechnest du den Abstand  vom Ursprung aus:
vom Ursprung aus:
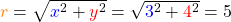 .
.
In Polarform sieht  also so aus
also so aus
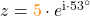 .
.
Polarkoordinaten auf kartesische Koordinaten
Diesmal hast du eine komplexe Zahl  in Polarkoordinaten gegeben
in Polarkoordinaten gegeben
 .
.
Um die kartesische Koordinaten  und
und 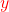 zu bestimmen, rechnest du
zu bestimmen, rechnest du
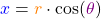 und
und
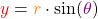 .
.
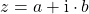 ;
; 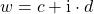
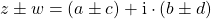
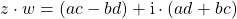
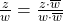
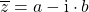 ;
; 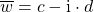
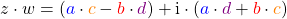 .
.
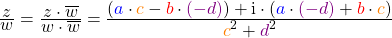 .
.
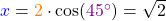 und
und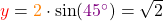 .
.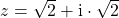 .
.