Abstand zweier Punkte
In diesem Beitrag erklären wir dir, wie du den Abstand zweier Punkt berechnest. Noch schneller verstehst du die Berechnung zwischen zwei Punkten mit unserem Video .
Inhaltsübersicht
Abstand zweier Punkte einfach erklärt
Der Abstand zwischen zwei Punkten im Raum entspricht der kürzesten Verbindungsstrecke zwischen den Punkten, also eine gerade Linie. Hier siehst du die beiden Formeln für die Ebene und den Raum:
2 Dimensionen
Liegen die beiden Punkte auf einer Ebene, also im zweidimensionalen Raum, dann beträgt der Abstand  der Punkte
der Punkte  und
und  :
:

3 Dimensionen
Im dreidimensionalen Raum erweitert man die Formel einfach um die z-Koordinaten der Punkte. Die Distanz zwischen  und
und  kann man daher so berechnen:
kann man daher so berechnen:

Abstand zweier Punkte berechnen
Als nächstes wollen wir in zwei Beispielen ausführlich vorrechnen, wie man den Abstand zwischen zwei Punkten berechnet. Das machen wir sowohl für Punkte, die in einer zweidimensionalen Ebene liegen als auch für solche, die sich in einem dreidimensionalen Raum befinden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispielaufgabe 1:
Wir suchen den Abstand  der Punkte
der Punkte 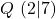 und
und  .
.
Um diese Aufgabe zu lösen, benötigen wir die Formel für zwei Dimensionen, denn die einzelnen Punkte haben zwei Koordinaten. Sie setzen wir in die 2D-Formel für den Abstand ein. Anschließend rechnen wir erst die Klammern aus und quadrieren sie. Danach bilden wir die Summe dieser Quadrate und ziehen zum Schluss die Wurzel.

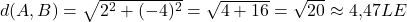
Für den Abstand von Punkt  zu Punkt
zu Punkt  erhalten wir eine Lösung von circa 4,47 Längeneinheiten (z.B. Meter, Zentimeter, … ).
erhalten wir eine Lösung von circa 4,47 Längeneinheiten (z.B. Meter, Zentimeter, … ).
Beispielaufgabe 2
Wir suchen den Abstand  der Punkte
der Punkte  und
und  .
.
Bei dieser Aufgabe befinden wir uns in einem dreidimensionalen Raum, denn jeder Punkt besitzt drei Koordinaten. Zur Lösung brauchen wir also die 3D-Formel für den Abstand Punkt Punkt. Nach dem Einsetzen der Koordinaten ziehen wir diese wiederum paarweise voneinander ab und quadrieren die Ergebnisse. Zum Schluss addieren wir alle Quadrate und ziehen die Wurzel aus der Summe.



Der Abstand zwischen Punkt  und Punkt
und Punkt  beträgt circa 3,74 LE.
beträgt circa 3,74 LE.
Abstandsrechnungen in der Geometrie
In der Geometrie kannst du nicht nur den Abstand zweier Punkte berechnen, sondern auch Abstände zwischen anderen und verschiedenen Formen. Zum Glück haben wir zu all diesen Themen eigene Beiträge für dich:
- Abstand zwischen einem Punkt und einer Geraden (Abstand Punkt Gerade )
- Abstand zwischen zwei Geraden (Abstand Gerade Gerade
)
- wenn die Geraden parallel verlaufen (Abstand Gerade Gerade )
- wenn die Geraden windschief zueinander stehen (Abstand windschiefer Geraden )
- Abstand eines Punktes von einer Ebene (Abstand Punkt Ebene )
- Abstand zwischen einer Geraden und einer Ebene (Abstand Gerade Ebene )
Abstände mit der euklidischen Distanz
Die Formeln, die du jetzt kennst, sind nur Spezialfälle der Formel für die euklidische Distanz. Mit ihr kannst du den Abstand zwischen zwei Punkten in Räumen mit noch mehr als drei Dimensionen berechnen. Die Formel lautet:

Abstand zweier Punkte — häufigste Fragen
(ausklappen)
Abstand zweier Punkte — häufigste Fragen
(ausklappen)-
Was bedeutet der Abstand zwischen zwei Punkten im Koordinatensystem genau?Der Abstand zwischen zwei Punkten im Koordinatensystem ist die Länge der kürzesten Verbindung zwischen den Punkten. Du misst also die Strecke der Geraden von
 nach
nach  , nicht den Weg entlang der x- und y-Richtung. Deshalb beschreibt der Abstand, wie weit die Punkte wirklich auseinanderliegen.
, nicht den Weg entlang der x- und y-Richtung. Deshalb beschreibt der Abstand, wie weit die Punkte wirklich auseinanderliegen.
-
Wie rechne ich den Abstand zwischen zwei Punkten in 2D aus, wenn ich nur x- und y-Koordinaten habe?Den Abstand in 2D berechnest du mit
 . Zuerst bildest du
. Zuerst bildest du  und
und  . Danach quadrierst du beide und ziehst die Wurzel. Zum Beispiel:
. Danach quadrierst du beide und ziehst die Wurzel. Zum Beispiel:  ,
,  :
:  .
.
-
Wie rechne ich den Abstand zwischen zwei Punkten in 3D aus, wenn auch eine z-Koordinate dabei ist?Den Abstand in 3D berechnest du mit
 . Du gehst wie in 2D vor, nur mit einer dritten Differenz. Zum Beispiel:
. Du gehst wie in 2D vor, nur mit einer dritten Differenz. Zum Beispiel:  ,
,  :
:  .
.
-
Warum kommt bei der Abstandsformel am Ende dasselbe raus, egal ob ich x(2) minus x(1) oder x(1) minus x(2) rechne?Bei der Abstandsformel ist die Reihenfolge egal, weil die Differenzen quadriert werden. Ein Vorzeichen verschwindet beim Quadrieren, denn es gilt
 . Deshalb liefert
. Deshalb liefert  denselben Beitrag wie
denselben Beitrag wie  . Zum Beispiel:
. Zum Beispiel:  und
und  .
.
-
Wie kann ich die Abstandsformel in 2D mit dem Satz des Pythagoras herleiten?Die Abstandsformel in 2D leitest du her, indem du aus
 und
und  ein rechtwinkliges Dreieck konstruierst. Dabei sind die Katheten
ein rechtwinkliges Dreieck konstruierst. Dabei sind die Katheten  und
und  , die Hypotenuse ist der Abstand
, die Hypotenuse ist der Abstand  . Nach Pythagoras gilt
. Nach Pythagoras gilt  , daher
, daher  .
.
Herleitung: Abstand zwischen zwei Punkten
Du fragst dich vielleicht, wie man auf die beiden Formeln kommt, mit denen man den Abstand zweier Punkte berechnen kann. Das geht ganz einfach mit dem Satz von Pythagoras. Zum besseren Verständnis erklären wir dir sowohl die Herleitung der Abstandsformel in der Ebene als auch für drei Dimensionen. Aber eigentlich handelt es sich beide Male um den gleichen Rechenweg.