Lineare Funktionen
Du willst alles über Lineare Funktionen wissen? Hier in diesem Artikel erklären wir dir alles zur Funktionsgleichung, zur Steigung und zu den Spezialfällen. Am Ende des Textes findest du einige Aufgaben mit Lösungsvorschlägen zum selber üben.
Statt einen langen Text zu lesen, willst du lineare Funktionen lieber schnell verstehen? Dann schau dir einfach dieses Video an.
Inhaltsübersicht
Lineare Funktionen einfach erklärt
Lineare Funktionen gehören zu den einfachsten Funktionstypen. Sie veranschaulichen einen linearen Zusammenhang zwischen der Definitionsmenge und dem Wertebereich . Du kannst diesen Zusammenhang immer in Form einer Gerade graphisch darstellen. Dabei gibt es verschiedene Arten von Geraden: Sie können steigen, fallen, senkrecht oder waagrecht im Koordinatensystem liegen. Letzteres schauen wir uns später genauer an. Linear bedeutet aber in jedem dieser Fälle, dass du eine gleichmäßige Zu- oder Abnahme gegeben hast.
Hinweis: Einen leichteren Einstieg ins Thema findest du in unserem Beitrag Lineare Funktionen einfach erklärt .
Lineare Funktionen – Was ist das?
Was genau lineare Funktionen sind, kann man sich am besten an einem Beispiel im Supermarkt vorstellen. Angenommen, eine Tafel Schokolade kostet 1,20€. Kaufst du zwei Tafeln dieser Schokolade, so musst du 2,40€ bezahlen. Es besteht also ein direkter Zusammenhang zwischen der Anzahl an Schokoladentafeln und dem Preis. Diesen Zusammenhang kannst du auf verschiedene Arten darstellen. Die einfachste Möglichkeit ist eine Wertetabelle.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Wertetabelle Zusammenhang zwischen Anzahl der gekauften Schokoladentafeln und Preis
| Anzahl | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Preis | 0 | 1,20€ | 2,40€ | 3,60€ | 4,80€ | 6,00€ | 7,20€ | 8,40€ | 9,60€ | 10,80€ | 12,00€ |
Du kannst die Werte auch graphisch veranschaulichen. Dazu zeichnest du alle Punkte der Wertetabelle in ein Koordinatensystem, das die Anzahl an Tafeln auf der x-Achse abträgt und den Preis auf der y-Achse. Wenn du die Punkte verbindest, bekommst du eine Ursprungsgerade mit Steigung  .
.
Diesen Zusammenhang kann man mathematisch auch in Formeln ausdrücken:
Preis = 1,20€ mal Anzahl
 €
€ 
Steigung
Die Steigung  einer linearen Funktion gibt an, wie schnell sich die Funktionswerte
verändern. Dabei gibt es drei verschiedene Möglichkeiten:
einer linearen Funktion gibt an, wie schnell sich die Funktionswerte
verändern. Dabei gibt es drei verschiedene Möglichkeiten:
-
 : Die Gerade steigt.
: Die Gerade steigt. -
 : Du erhältst eine waagerechte Gerade.
: Du erhältst eine waagerechte Gerade. -
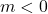 : Die Gerade fällt.
: Die Gerade fällt.
Den Fall  werden wir genauer im Abschnitt zu den waagrechten und senkrechten Geraden untersuchen. Jetzt nehmen wir an, dass die Steigung immer positiv oder negativ ist. Um sie zu bestimmen, gibt es verschiedene Möglichkeiten.
werden wir genauer im Abschnitt zu den waagrechten und senkrechten Geraden untersuchen. Jetzt nehmen wir an, dass die Steigung immer positiv oder negativ ist. Um sie zu bestimmen, gibt es verschiedene Möglichkeiten.
Am einfachsten ist es direkt am Funktionsgraphen mithilfe eines Steigungsdreiecks .
Dazu wählst du zwei beliebige Punkte  und
und  auf der Geraden und zeichnest das dadurch festgelegte rechtwinklige Dreieck ein. Die Steigung der linearen Funktion kannst du nun als Differenzenquotient berechnen:
auf der Geraden und zeichnest das dadurch festgelegte rechtwinklige Dreieck ein. Die Steigung der linearen Funktion kannst du nun als Differenzenquotient berechnen:

In unserem Beispiel-Bild haben wir dazu die Punkte  und
und 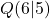 gewählt. Die Steigung beträgt daher
gewählt. Die Steigung beträgt daher
 .
.
Alternativ kannst du die Steigung von linearen Funktionen berechnen, wenn du zwei Punkte  und
und  gegeben hast, oder beispielsweise auch einen Punkt und den y-Achsenabschnitt
gegeben hast, oder beispielsweise auch einen Punkt und den y-Achsenabschnitt  . Wie genau, erklären wir dir im separaten Artikel Steigung berechnen
.
. Wie genau, erklären wir dir im separaten Artikel Steigung berechnen
.
Manchmal interessiert man sich in der Mathematik auch für den Steigungswinkel
 . Das ist der positive Winkel, den die Funktion mit der x-Achse einschließt. Du kannst ihn mit dieser Formel berechnen:
. Das ist der positive Winkel, den die Funktion mit der x-Achse einschließt. Du kannst ihn mit dieser Formel berechnen:
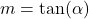 und
und 
Dabei ist der Arcustangens
die Umkehrfunktion
der Tangens-Funktion. In unserem vorherigen Beispiel mit Steigung  beträgt der Steigungswinkel daher
beträgt der Steigungswinkel daher  .
.
y-Achsenabschnitt
Nun wollen wir noch das  in der Funktionsgleichung
in der Funktionsgleichung  genauer untersuchen. Es gibt den y-Achsenabschnitt
an, genauer gesagt den Punkt, an dem die Gerade die y-Achse schneidet. Wenn du also beispielsweise die Geradengleichung
genauer untersuchen. Es gibt den y-Achsenabschnitt
an, genauer gesagt den Punkt, an dem die Gerade die y-Achse schneidet. Wenn du also beispielsweise die Geradengleichung  betrachtest, dann hat sie den y-Achsenabschnitt bei
betrachtest, dann hat sie den y-Achsenabschnitt bei 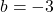 .
.
Merke: Lineare Funktionen mit  heißen Ursprungsgeraden. Sie veranschaulichen stets eine direkte Proportionalität.
heißen Ursprungsgeraden. Sie veranschaulichen stets eine direkte Proportionalität.
Nullstellen berechnen: Lineare Funktionen
Wenn du wissen willst, wo lineare Funktionen die x-Achse schneiden, dann musst du ihre Nullstellen berechnen. Das heißt, du bestimmst

und löst nach  auf. Für die Funktion
auf. Für die Funktion  erhältst du dann zum Beispiel
erhältst du dann zum Beispiel


Somit hat die Funktion bei  eine Nullstelle.
eine Nullstelle.
Ausführlich erklärt findest du das im Artikel Nullstellen berechnen . Dort zeigen wir dir auch mehrere Beispiele, wie du die Nullstellen berechnen kannst.
Lineare Funktionen Graf: Gerade
Lineare Funktionen haben als Funktionsgraphen immer eine Gerade. Am einfachsten zeichnest du sie, indem du zwei Punkte auf der Geraden berechnest, und diese dann verbindest. Verwende dazu am besten den y-Achsenabschnitt mit den Koordinaten  .
.
Merke: Eine Gerade ist durch zwei Punkte eindeutig definiert!
Alternativ kannst du auch einen Punkt wählen und hier die Steigung abtragen, indem du entsprechend viele Kästchen nach rechts beziehungsweise oben läufst. Im Bild bei einem y-Achsenabschnitt von  und einer Steigung
und einer Steigung 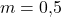 bedeutet das, dass du zwei Kästchen nach rechts und ein Kästchen nach oben gehst, um den nächsten Punkt zu erhalten.
bedeutet das, dass du zwei Kästchen nach rechts und ein Kästchen nach oben gehst, um den nächsten Punkt zu erhalten.
Lineare Funktionsgleichung bestimmen
Möchtest du lineare Funktionen anhand ihrer Funktionsgleichung untersuchen, so gehst du ganz unterschiedlich vor. Kennst du den Funktionsgraphen, also die Gerade, dann kannst du den Funktionsterm direkt ablesen, indem du  und
und  bestimmst. Aus den Koordinaten zweier Punkte kannst du die Funktionsgleichung auch einfach berechnen.
bestimmst. Aus den Koordinaten zweier Punkte kannst du die Funktionsgleichung auch einfach berechnen.
Alle Möglichkeiten, wie du dabei vorgehen kannst, erklären wir dir ausführlich im Artikel Funktionsgleichung .
Besonderheiten waagrechter und senkrechter Geraden
Eine Besonderheit stellen die waagrechten und die senkrechten Geraden im Koordinatensystem dar. Waagrechte lineare Funktionen haben immer die Steigung  und damit die Funktionsgleichung
und damit die Funktionsgleichung  . Hier kannst du kein Steigungsdreieck einzeichnen. Auch der Steigungswinkel ist hier konstant
. Hier kannst du kein Steigungsdreieck einzeichnen. Auch der Steigungswinkel ist hier konstant  .
.
Das andere Extremum sind die senkrechten Geraden. Hierbei handelt es sich aber klassischerweise nicht um lineare Funktionen, da hier einem x-Wert alle y-Werte zugeordnet werden. Senkrechte Geraden haben also immer die Funktionsgleichung  . Ihre Steigung beträgt sozusagen unendlich und ihr Steigungswinkel ist immer
. Ihre Steigung beträgt sozusagen unendlich und ihr Steigungswinkel ist immer  .
.
Lage von Geraden
Es gibt zwei verschiedene Möglichkeiten, wie zwei lineare Funktionen in einem zweidimensionalen Koordinatensystem zueinander liegen können. Entweder sind zwei lineare Funktionen parallel oder sie haben einen eindeutigen Schnittpunkt. Dass zwei lineare Funktionen parallel sind, erkennst du immer daran, dass sie dieselbe Steigung haben.
Hast du zwei parallele lineare Funktionen gegeben, so musst du lediglich unterscheiden, ob sie echt parallel sind oder identisch. Das erkennst du sofort am y-Achsenabschnitt. Ist er verschieden, haben die Geraden keinen einzigen gemeinsamen Punkt.
Dass die Geraden im Bild echt parallel sind, siehst du direkt am unterschiedlichen y-Achsenabschnitt in den Funktionsgleichungen


Ob zwei lineare Funktionen identisch oder echt parallel sind, kannst du auch mit der Punktprobe überprüfen. Dazu setzt du einen Punkt der ersten Gerade in die zweite ein und überprüfst, ob du ein sinnvolles Ergebnis erhältst. Allgemein kannst du die Punktprobe immer dann verwenden, wenn du wissen willst, ob ein bestimmter Punkt auf der Gerade liegt, oder nicht.
Schnittpunkt zweier Geraden
Angenommen du hast zwei lineare Funktionen gegeben, und möchtest ihren Schnittpunkt bestimmen. Dann setzt du sie am besten gleich und berechnest  . Das zeigen wir dir ausführlich im Artikel Schnittpunkt zweier Geraden.
. Das zeigen wir dir ausführlich im Artikel Schnittpunkt zweier Geraden.
Schnittwinkel zweier Geraden
Auch den Schnittwinkel
kannst du für zwei lineare Funktionen berechnen, insbesondere, wenn sich die beiden Geraden in einem  -Winkel schneiden. Das erkennst du an der Steigung: Hat die erst Gerade die Steigung
-Winkel schneiden. Das erkennst du an der Steigung: Hat die erst Gerade die Steigung  , so ist die Steigung der zweiten linearen Funktion
, so ist die Steigung der zweiten linearen Funktion  .
.
Lineare Funktionen Aufgaben
Im Folgenden findest du verschiedene Übungen mit Lösungen zum Thema Lineare Funktionen.
Aufgabe 1
a) Zeichne die Gerade durch die beiden Punkte  und
und  .
.
b) Bestimme die zugehörige Funktionsgleichung.
c) Berechne den Steigungswinkel der Funktion.
Aufgabe 2
Überprüfe zwei lineare Funktionen auf ihre Lage im Koordinatensystem. Berechne gegebenenfalls den Schnittpunkt. Schneiden sie sich in einem besonderen Winkel?
a)  und
und 
b)  und
und 
Lösung Aufgabe 1
b) Durch Ablesen sieht man sofort, dass  gelten muss. Außerdem ist die Gerade fallend, weswegen
gelten muss. Außerdem ist die Gerade fallend, weswegen 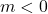 sein muss. Um die Steigung zu berechnen, betrachten wir das Steigungsdreieck, das die Gerade mit den beiden Koordinatenachsen einschließt. Hier gehst du vier Schritte nach rechts und drei nach unten. Somit ist
sein muss. Um die Steigung zu berechnen, betrachten wir das Steigungsdreieck, das die Gerade mit den beiden Koordinatenachsen einschließt. Hier gehst du vier Schritte nach rechts und drei nach unten. Somit ist  und
und
 .
.
c) Der Steigungswinkel für eine Gerade mit negativer Steigung berechnet sich aus  . Hier ist daher
. Hier ist daher

Lösung Aufgabe 2
a) Die beiden Funktionen haben eine unterschiedliche Steigung, nämlich 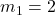 und
und  . Anhand der Steigung erkennt man, dass die Geraden senkrecht aufeinander stehen. Um ihren Schnittpunkt zu berechnen, setzen wir sie gleich
. Anhand der Steigung erkennt man, dass die Geraden senkrecht aufeinander stehen. Um ihren Schnittpunkt zu berechnen, setzen wir sie gleich

Auflösen ergibt  . Setzen wir diesen Wert in eine der beiden Gleichungen ein, erhalten wir
. Setzen wir diesen Wert in eine der beiden Gleichungen ein, erhalten wir  . Der Schnittpunkt liegt bei
. Der Schnittpunkt liegt bei  .
.
b) Die Geraden sind echt parallel, da sie dieselbe Steigung, aber einen unterschiedlichen y-Achsenabschnitt haben.
Quadratische Funktionen
Neben den linearen, gibt es auch noch die quadratischen Funktionen. Du erkennst sie im Koordinatensystem daran, dass sie als Funktionsgraph eine Parabel haben. Schau dir unbedingt unser Video dazu an, um alles Wichtige über quadratische Funktionen zu erfahren!


 und
und 






