Video

Quiz

Hier geht's zum Video „Mechanische Arbeit“

Kinetische Energie

Wichtige Inhalte in diesem Video

Was ist kinetische Energie?

Kinetische Energie Formel

Kinetische Energie Einheit

Kinetische Energie berechnen

Kinetische Energie Beispiel

Welche kinetische Energie besitzt ein fahrendes Auto? Was ist der Unterschied zwischen der Translationsenergie und der Rotationsenergie? Wenn dich diese Fragen interessieren, dann bist du hier genau richtig. Wir erklären dir, was die kinetische Energie bedeutet und wie du sie berechnen kannst.

Schau dir auf jeden Fall unser Video zur kinetischen Energie an, wenn du das Wichtigste zum Thema schnell und verständlich im Videoformat verstehen willst.

Inhaltsübersicht

Was ist kinetische Energie?

im Videozur Stelle im Video springen

Als kinetische Energie (E_kin) kannst du die Energie bezeichnen, die bei der Bewegung eines Körpers entsteht. Deshalb kannst du sie auch als Bewegungsenergie oder Geschwindigkeitsenergie bezeichnen.

Die kinetische Energie findet, genau wie die potentielle Energie , bestimmt in deinem täglichen Leben eine häufige Anwendung. So besitzt beispielsweise dein Fahrrad eine kinetische Energie, wenn die notwendige Arbeit aufgebracht wird, um es von der Stelle zu bewegen. Diese Arbeit kann einerseits zum Beispiel durch eine andere Person, die dich anschiebt, aufgewendet werden. Aber sie wird auch aufgewendet, wenn du selbst in die Pedale trittst.

Der Artikel mechanische Arbeit und konservative Kräfte gibt dir zur Wiederholung einen guten Überblick über den Begriff der Arbeit.

Wenn du die kinetische Energie eines starren Körpers bestimmen willst, dann musst du die Summe aus der Translationsenergie und der Rotationsenergie um den Schwerpunkt berechnen. Die Besonderheit eines starren Körpers besteht darin, dass er aus mehreren Punktmassen besteht, die in einem festen Abstand zueinander stehen.

Kinetische Energie Formel

im Videozur Stelle im Video springen

Die Formel für die kinetische Energie (E_kin Formel) lautet:

$E_{Kin} = \frac {1}{2} m \cdot v^2$ .

Sie ist also von der Masse des Körpers und von seiner Geschwindigkeit abhängig.
Das bedeutet in Bezug auf das Fahrrad-Beispiel: Je schwerer dein Fahrrad ist und je schneller du damit fährst, desto höher ist seine kinetische Energie.

Um die kinetische Energie aus der Beschleunigungsarbeit herzuleiten, benötigst du zuerst die relevanten Formeln. Die Arbeit bei konstanter Kraft wird mit $W=F \cdot s$ angegeben. Die allgemeine Formulierung der Kraft ist $F=m \cdot a$ und den Weg kannst du als $s=\frac {1}{2} a \cdot t^2$ beschreiben.

Durch Einsetzen dieser beiden Formeln in die Formel für die Arbeit erhältst du:

$W=ma \cdot \frac {1}{2}at^2$ .

Mit dem Zusammenhang $v=a\cdot t$ ergibt sich:

$W= \frac {1}{2} m \cdot v^2$ .

Wenn keine Bewegung vorherrscht, ist die kinetische Energie gleich Null. Folglich kann die Höhe der geleisteten Beschleunigungsarbeit mit der Höhe der kinetischen Energie gleichgesetzt werden.
Es gilt:

$W= \frac {1}{2} m \cdot v^2 = E_{Kin}$

Kinetische Energie Einheit

im Videozur Stelle im Video springen

Die Einheit der kinetischen Energie (E_kin Einheit) ist das Joule mit Einheitenzeichen . Diese abgeleitete Einheit kannst du auch in Basiseinheiten ausdrücken als:

$1 J = 1 \frac {kg \cdot m^2}{s^2}$ .

Diese Form ergibt sich durch Multiplikation der Einheiten der Masse () und der Geschwindigkeit im Quadrat ( $\frac {m^2}{s^2}$ ) aus der Formel der Bewegungsenergie.

Kinetische Energie berechnen

im Videozur Stelle im Video springen

Zur Berechnung der kinetischen Energie (E_kin)eines Körpers benötigst du lediglich die Masse und die Geschwindigkeit dieses Körpers.

Wenn du nun ein physikalisches System wie einen rotierenden starren Körper mit einem bestimmten Schwerpunkt betrachtest, musst du eine Unterscheidung in Translationsenergie und Rotationsenergie vornehmen.

Translationsenergie

Die Translation beschreibt in der Kinetik die Bewegung aller Massepunkte eines physikalischen Systems in eine bestimmte Richtung. Das heißt, dass zu einem gegebenen Zeitpunkt alle Punkte dieselbe Geschwindigkeit und Beschleunigung besitzen.

Kinetische Energie, Translationsenergie, starrer Körper — Translationsenergie eines starren Körpers

Die Translationsenergie ist folglich die Energie einer translatorischen Bewegung. Somit kann die Translationsenergie eines nicht rotierenden Systems mit der Bewegungsenergie Formel gleichgesetzt werden ( $E_{Kin}=E_{Trans}=\frac {1}{2} m \cdot v^2$ ).

Rotationsenergie

Wenn das physikalische System nun zusätzlich eine Rotation um eine gegebene Achse aufweist, musst du zudem noch die Rotationsenergie dieses Systems betrachten. Diese ist abhängig vom Trägheitsmoment und von der Winkelgeschwindigkeit $\omega$ des starren Körpers.

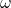Rotationsenergie, kinetische Energie, starrer Körper — Rotationsenergie eines starren Körpers

Für die Rotationsenergie ergibt sich somit:

$E_{Rot} = \frac {1}{2}J\omega^2$ .

Um nun die Gesamtenergie eines starren Körpers zu berechnen, musst du die Translationsenergie und die Rotationsenergie addieren:

$E_{Kin,Ges} = E_{Trans} + E_{Rot}$

Mittlere kinetische Energie

Zur Berechnung der mittleren kinetischen Energie ( $\overline {E_{Kin}}$ ) benötigst du die mittleren Geschwindigkeit der betrachteten Massepunkte. Daraus kannst du dann die mittlere kinetische Energie bestimmen:

$\overline {E_{Kin}}= \frac{1}{2}m \cdot \overline {v^2}$ .

Diese Berechnung erleichtert dir insbesondere das Ermitteln der mittleren kinetischen Energie eines Gases, da die nicht jede einzelne Geschwindigkeit der Gasteilchen miteinbezogen werden muss.

Kinetische Energie Beispiel

im Videozur Stelle im Video springen

Betrachten wir als Anwendungsbeispiel die kinetische Energie (E_kin)eines Autos. Das Auto besitzt ein Gewicht von Tonnen. Wenn das Auto zu Beginn still steht, wird noch keine Arbeit aufgewendet. Es besitzt folglich auch noch keine kinetische Energie. Betätigst du nun das Gaspedal, erfährt das Auto eine Beschleunigungsarbeit und fährt los.

Bei einer Masse des Autos von 1500 kg und einer Geschwindigkeit von $50 \frac {km}{h}$ soll die kinetische Energie des Autos bestimmt werden. Die Geschwindigkeit des Autos in $\frac {m}{s}$ beträgt ca. $\frac {50}{3,6} \approx 13,89 \frac {m}{s}$ . Somit erhältst du für die Bewegungsenergie:

$E_{Kin}=\frac {1}{2} \cdot 1500 kg\cdot ({13,89 \frac {m}{s}})^2 \approx 144.699,1 \frac {kg \cdot m^2}{s^2} = 144.699,1 J$ .

zur Videoseite: Kinetische Energie

Beliebte Inhalte aus dem Bereich Dynamik

Kinetische Energie

Potentielle Energie

Bewegungsenergie

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .