Unelastischer Stoß
Der unelastische Stoß kann in eine vollkommene unelastische und in eine unelastische Art für zwei Körper unterteilt werden. In unserem Video erklären wir dir in kürzester Zeit den unelastischen Stoß. Dazu lernst du wichtige Sonderfälle kennen.
Inhaltsübersicht
Unelastischer Stoß Definition
Bei einem Stoß treffen zwei Körper aufeinander und es kommt zu einer Wechselwirkung zwischen diesen. Wird dabei ein Teil der kinetischen Energie in innere Energie umgewandelt, so wird von einem unelastischen Stoß gesprochen. Eine Umwandlung findet zum Beispiel bei Deformation oder bei Wärmeentwicklung der Körper statt. Synonyme zu unelastisch sind inelastisch und plastisch.
Ein unelastischer Stoß wird als vollkommen unelastisch bezeichnet, wenn die zwei Körper nach dem Stoß einander „kleben“ und sich mit der gleichen Geschwindigkeit in die gleiche Bewegungsrichtung weiterbewegen. Falls das der Fall ist, wird der maximal mögliche Anteil der kinetischen Energie in die innere Energie umgewandelt. Trifft das nicht zu, sprechen wir von einem normalen unelastischen Stoß.
Unelastischer Stoß Formel
Bei der Aufstellung der Formel für den unelastischen Stoß unterscheiden sich die beiden Arten kaum. In beiden Fällen gilt der Impulserhaltungssatz, weil die äußeren Kräfte vernachlässigt werden. Die mathematische Formulierung ist hier ähnlich dem elastischen Stoß. Falls du mehr über diese Art des Stoßes wissen möchtest, ist hier das Video verlinkt. Ebenfalls haben wir einen kompletten Artikel über die Impulserhaltung, welchen du hier findest. Der Impulserhaltungssatz lautet nun:

Die Geschwindigkeiten
vor dem Stoß sind  und nach dem Stoß
und nach dem Stoß  für beide Körper. Deren Massen werden durch
für beide Körper. Deren Massen werden durch  beschrieben. Da zwar die Massen und Anfangsgeschwindigkeiten für die Körper bekannt sind, werden meistens die Geschwindigkeiten nach dem unelastischen Stoß gesucht. Um diese berechnen zu können, wird eine zweite Gleichung benötigt. Für den elastischen Stoß gilt die Energieerhaltung
. Auch bei dem unelastischen kann diese angewandt werden, muss aber ergänzt werden. Laut der Definition wird ein Teil der anfänglich existierenden kinetischen Energie in innere Energie, beziehungsweise Verformungsenergie umgewandelt. So haben die die Körper nach dem Stoß eine Bewegungs- und innere Energie. Ansonsten wäre der Stoß nicht inelastisch. Den Zusammenhang kann mathematisch so formuliert werden:
beschrieben. Da zwar die Massen und Anfangsgeschwindigkeiten für die Körper bekannt sind, werden meistens die Geschwindigkeiten nach dem unelastischen Stoß gesucht. Um diese berechnen zu können, wird eine zweite Gleichung benötigt. Für den elastischen Stoß gilt die Energieerhaltung
. Auch bei dem unelastischen kann diese angewandt werden, muss aber ergänzt werden. Laut der Definition wird ein Teil der anfänglich existierenden kinetischen Energie in innere Energie, beziehungsweise Verformungsenergie umgewandelt. So haben die die Körper nach dem Stoß eine Bewegungs- und innere Energie. Ansonsten wäre der Stoß nicht inelastisch. Den Zusammenhang kann mathematisch so formuliert werden:

Bei dieser Gleichung muss gelten:
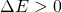
Das  ist die Energiedifferenz, die von kinetischer Energie in Verformungsenergie umgewandelt wird. Dadurch kommt eine weitere unbekannte Variable in die Gleichungen. Jetzt wird die Unterscheidung in die zwei Arten des plastischen Stoßes wichtig. Denn bei dem zentralen vollkommenen inelastischen Stoß können die Geschwindigkeiten nach dem Stoß gleichgesetzt werden, da die Körper ja aneinander „kleben“. Beim nicht vollkommenen Stoß muss in der Aufgabenstellung weitere Angaben zu den Variablen gemacht werden, um Berechnungen machen zu können. Diese laufen dann ähnlich zum elastischen Fall ab. Deshalb ist es sinnvoll nur den vollkommenen inelastischen Stoß weiter zu betrachten. Hier kann folgende Vereinfachung getroffen werden:
ist die Energiedifferenz, die von kinetischer Energie in Verformungsenergie umgewandelt wird. Dadurch kommt eine weitere unbekannte Variable in die Gleichungen. Jetzt wird die Unterscheidung in die zwei Arten des plastischen Stoßes wichtig. Denn bei dem zentralen vollkommenen inelastischen Stoß können die Geschwindigkeiten nach dem Stoß gleichgesetzt werden, da die Körper ja aneinander „kleben“. Beim nicht vollkommenen Stoß muss in der Aufgabenstellung weitere Angaben zu den Variablen gemacht werden, um Berechnungen machen zu können. Diese laufen dann ähnlich zum elastischen Fall ab. Deshalb ist es sinnvoll nur den vollkommenen inelastischen Stoß weiter zu betrachten. Hier kann folgende Vereinfachung getroffen werden:

Somit verändern sich der Impuls– und der Energieerhaltungssatz zu:


Nun können die Gleichungen umgestellt und nach den zu suchenden Variablen aufgelöst werden. Wir haben die wichtigen Variablen in Formeln für dich herausgeschrieben. Die Verformungsenergie ergibt sich zu:

Die Geschwindigkeit der zwei aneinander „klebenden“ Körpern ist nach dem Stoß:

Das wären die wichtigsten Formeln für den unelastischen Stoß.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Unelastischer Stoß Grenzfälle
Es können insgesamt drei Grenzfälle für den inelastischen Stoß betrachtet werden. Der erste kommt zustande, wenn die Masse des ersten Körpers viel kleiner ist, als die des zweiten Objektes. Das zweite ruht und hat daher eine Geschwindigkeit von  . Beide Objekte ruhen nach der Wechselwirkung und die komplette kinetische Energie wird in innere Energie umgesetzt.
. Beide Objekte ruhen nach der Wechselwirkung und die komplette kinetische Energie wird in innere Energie umgesetzt.


Im zweiten Sonderfall haben beide Körper die gleiche Masse m und Körper 2 ruht vor dem unelastischen Stoß. Nach der Wechselwirkung bewegen sich beide Objekte mit der halben Geschwindigkeit von dem ersten Körper in die gleiche Bewegungsrichtung weiter.


In dem letzten Sonderfall zur Anwendung der unelastischen Stoß Formel haben wieder die Körper eine gleiche Masse von  . Die zwei Objekte haben die gleiche Geschwindigkeit vor dem Stoß. Diese ist aber entgegengesetzt. Körper 1 bewegt sich nach rechts und Körper 2 nach links. Die Bewegung nach links wird mit einem negativen Vorzeichen gekennzeichnet.
. Die zwei Objekte haben die gleiche Geschwindigkeit vor dem Stoß. Diese ist aber entgegengesetzt. Körper 1 bewegt sich nach rechts und Körper 2 nach links. Die Bewegung nach links wird mit einem negativen Vorzeichen gekennzeichnet.


Die zwei physikalischen Objekte haben nach dem Stoß eine Geschwindigkeit von null, sie ruhen also. Hier wird die gesamte kinetische Energie in innere Energie umgewandelt.


