Erzwungene Schwingung
Die harmonische Schwingung hast du bereits kennengelernt? Jetzt zeigen wir dir die erzwungene Schwingung. Wie man diese durch eine Bewegungsgleichung darstellen und lösen kann sowie welche Bedingungen im Resonanzfall gelten müssen, erfährst du genau hier! Des Weiteren berechnen wir in einem Beispiel auch die Energie der erzwungenen Schwingung im Resonanzfall.
Du kannst dir Inhalte wesentlich einfach merken, wenn du sie sehen und hören kannst? Genau dafür ist unser Video da! Schau es dir unbedingt an!
Inhaltsübersicht
Erzwungene Schwingung Definition
Eine erzwungene Schwingung beschreibt ein schwingendes System (Oszillator ), welches durch eine äußere Kraft angetrieben wird. Wird das System von einer Erregerfrequenz angetrieben, so unterscheidet man drei Fälle. Entweder ist die Erregerfrequenz wesentlich kleiner oder größer als die Eigenfrequenz des Systems oder nahezu identisch. Im Gleichheitsfall spricht man vom Resonanzfall.
 ;
; 

Erzwungene Schwingung Bewegungsgleichung
Die Bewegungsgleichung eines gedämpften linearen Oszillators, der durch eine äußere zeitabhängige Kraft angetrieben wird, kann durch folgende Gleichung beschrieben werden:

Hierbei ist der Drehwinkel in Abhängigkeit der Zeit und beschreibt dementsprechend die momentane Auslenkung. Die Dämpfungskonstante wird durch den Buchstaben  repräsentiert und die Eigenfrequenz des ungedämpften Systems durch
repräsentiert und die Eigenfrequenz des ungedämpften Systems durch  .
.  und
und  stellen die Amplitude und die Frequenz der anregenden Kraft dar. Diese inhomogene Differentialgleichung kann mit Hilfe eines Exponentialansatzes gelöst werden. Wir wählen hierfür folgenden Ansatz
stellen die Amplitude und die Frequenz der anregenden Kraft dar. Diese inhomogene Differentialgleichung kann mit Hilfe eines Exponentialansatzes gelöst werden. Wir wählen hierfür folgenden Ansatz

Dabei beschreibt A die Amplitude der Schwingung nach dem Einschwingvorgang und  die Phasenverschiebung gegenüber der äußeren Anregung. Durch zweimaliges Differenzieren von
die Phasenverschiebung gegenüber der äußeren Anregung. Durch zweimaliges Differenzieren von  erhält man
erhält man
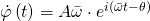

Setzt man dies nun in die Bewegungsgleichung ein, so führt dies zu folgendem Zusammenhang.


Aufsplitten der Gleichung in ihren Real- und Imaginärteil liefert
Realteil: 
Imaginärteil: 
Hieraus kann man nun die Amplitude A und die Phasenverschiebung  bestimmen. Unter Verwendung der Relation
bestimmen. Unter Verwendung der Relation  erhält man
erhält man


Die allgemeine Lösung des Systems ergibt sich, indem man dies in den Lösungsansatz  einsetzt
einsetzt


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Resonanzkurve
Die Resonanzkurve beschreibt die Amplitude der Schwingung A in Abhängigkeit der Erregerfrequenz  . Regt man das System mit verschiedenen Frequenzen an und misst dabei die Amplitude nach dem Einschwingvorgang, so erhält man folgende Kurven für verschiedene Dämpfungen
. Regt man das System mit verschiedenen Frequenzen an und misst dabei die Amplitude nach dem Einschwingvorgang, so erhält man folgende Kurven für verschiedene Dämpfungen  .
.
Ermittelt man die Frequenz, bei der die Amplitude maximal wird, so entspricht dies der Resonanzfrequenz  . Ist die Dämpfung
. Ist die Dämpfung 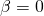 , so ist die Resonanzfrequenz gleich der Eigenfrequenz. Für eine größer werdende Dämpfung verschiebt sich die Resonanzfrequenz jedoch zu kleineren Frequenzen.
, so ist die Resonanzfrequenz gleich der Eigenfrequenz. Für eine größer werdende Dämpfung verschiebt sich die Resonanzfrequenz jedoch zu kleineren Frequenzen.
Resonanzfall
Bei einer erzwungenen Schwingung unterscheidet man abhängig von der Erregerfrequenz drei Fälle.
Dieser Fall beschreibt eine Anregung mit einer Frequenz die sehr viel kleiner ist als die Eigenfrequenz  des schwingenden Systems. Hierbei entspricht die Amplitude der Anregung ungefähr der Amplitude des schwingenden Systems, so dass das Verhältnis zwischen diesen ungefähr 1 ist. Der Phasenunterschied zwischen Erreger und schwingendem System ist ungefähr 0.
des schwingenden Systems. Hierbei entspricht die Amplitude der Anregung ungefähr der Amplitude des schwingenden Systems, so dass das Verhältnis zwischen diesen ungefähr 1 ist. Der Phasenunterschied zwischen Erreger und schwingendem System ist ungefähr 0.
-
 (Resonanzfall):
(Resonanzfall):
In diesem Fall entspricht die Erregerfrequenz  ungefähr der Eigenfrequenz
ungefähr der Eigenfrequenz  des schwingenden Systems. Man spricht auch vom Resonanzfall. Hierbei ist die Amplitude des schwingenden Systems größer, als die Amplitude des Erregers und der Phasenunterschied entspricht
des schwingenden Systems. Man spricht auch vom Resonanzfall. Hierbei ist die Amplitude des schwingenden Systems größer, als die Amplitude des Erregers und der Phasenunterschied entspricht  . Die Resonanzfrequenz lässt sich unter Verwendung der oberen Funktion
. Die Resonanzfrequenz lässt sich unter Verwendung der oberen Funktion  einfach berechnen. Da wir die Frequenz
einfach berechnen. Da wir die Frequenz  suchen, bei der die Amplitude maximal wird, kann diese einfach durch Differenzieren bestimmt werden
suchen, bei der die Amplitude maximal wird, kann diese einfach durch Differenzieren bestimmt werden

Berechnet man dies und formt die Gleichung nach um, so erhält man die Resonanzfrequenz

Hier ist die Erregerfrequenz  mit der das schwingende System angeregt wird viel größer als die Eigenfrequenz
mit der das schwingende System angeregt wird viel größer als die Eigenfrequenz  des Systems. Des Weiteren ist die Amplitude des schwingenden Systems sehr viel kleiner als die Amplitude des Erregers und die Phasenverschiebung entspricht ungefähr
des Systems. Des Weiteren ist die Amplitude des schwingenden Systems sehr viel kleiner als die Amplitude des Erregers und die Phasenverschiebung entspricht ungefähr  .
.
Energie im Resonanzfall
Da bei einer erzwungenen Schwingung das schwingende System beziehungsweise der Oszillator von außen durch eine Kraft angetrieben wird, findet eine Energieübertragung von dem Erreger auf den Oszillator statt. Hierbei hängt die Energie des Oszillators von der Dämpfung  ab. Bei großer Dämpfung wird mehr Energie an die Umgebung abgegeben, als dies bei kleinerer Dämpfung der Fall ist. Um die kinetische Energie
des Oszillators im Resonanzfall zu berechnen, geht man von der Winkelgeschwindigkeit
ab. Bei großer Dämpfung wird mehr Energie an die Umgebung abgegeben, als dies bei kleinerer Dämpfung der Fall ist. Um die kinetische Energie
des Oszillators im Resonanzfall zu berechnen, geht man von der Winkelgeschwindigkeit  aus
aus
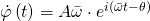

Da physikalisch nur eine reale Geschwindigkeit relevant ist, betrachten wir den Realteil dieser Gleichung

Hieraus lässt sich die maximale Geschwindigkeit  bestimmen
bestimmen

Die kinetische Energie

kann man bei einer Rotation durch die folgende Gleichung ausdrücken

Hierbei ist  der Radius und
der Radius und  die Winkelgeschwindigkeit. Setzt man nun die maximale Winkelgeschwindigkeit
die Winkelgeschwindigkeit. Setzt man nun die maximale Winkelgeschwindigkeit  von oben ein, führt dies auf
von oben ein, führt dies auf

Nun kann man die Energie des Oszillators im Resonanzfall, also wenn  , berechnen mit
, berechnen mit





