Spannenergie
Die Spannenergie findest du zum Beispiel in zusammengedrückten oder auseinandergezogenen Federn. Wie du das verstehen kannst, zeigen wir dir hier mit Beispielen und im Video !
Spannenergie einfach erklärt
Die Spannenergie ist eine Energieform, die in verformten Körpern steckt. So ein Körper kann zum Beispiel eine Feder sein. Wie hoch die Energie ist, hängt von der Federkonstante k und der Änderung der Ruhelänge x ab.
Einfach gesagt kannst du dir das so vorstellen: Wenn du eine Feder zusammendrückst oder auseinanderziehst, ist in ihr eine Spannenergie gespeichert. Sie hängt davon ab, wie stark die Feder ist (Federkonstante k) und wie weit du sie spannst oder stauchst (Änderung der Ruhelänge x).
Die Formel für die Spannenergie ESpann ist:
![\[\textcolor{purple}{E\mathsf{_{Spann}}} = \frac{1}{2} \cdot \textcolor{olive}{k} \cdot \textcolor{blue}{x^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bf233c38412b916c8ed086582652f4ee_l3.png "Rendered by QuickLaTeX.com")
Federkonstante k und Änderung der Ruhelänge x
Die Spannenergie wird von der Federkonstante k und der Änderung der Ruhelänge x bestimmt. Deshalb sind diese Größen für dich besonders wichtig.
- Die Federkonstante k sagt aus, wie leicht sich die Feder verformen lässt und wird manchmal auch als „D“ bezeichnet.
- Die Änderung der Ruhelänge x verrät dir, wie weit die Feder verformt wurde und wird manchmal auch als „s“ bezeichnet.
- Die Ruhelänge ist der Länge der Feder, bevor sie verformt wird.
Wie sich die Federkonstante und die Änderung der Ruhelänge auf die Spannenergie auswirken, schauen wir uns in zwei Beispielen an!
Einfluss der Federkonstante auf die Spannenergie
Um den Einfluss der Federkonstante auf die Spannenergie zu erkennen, stell dir folgendes Beispiel vor:
- Du hast zwei Federn mit unterschiedlicher Dicke am Boden befestigt.
- Nun drückst du auf beiden Federn einen Ball 5 cm herunter.
- Dann lässt du die Bälle los, sodass sie in die Luft fliegen.
Du erkennst, dass der Ball von Feder mit der höheren Federkonstante deutlich höher fliegt! Du kannst dir die Menge der gespeicherten Spannenergie in den Federn mit der Höhe der fliegenden Bälle vorstellen. Je höher der Ball fliegt, umso größer ist die gespeicherte Spannenergie der Feder. Also ist die Spannenergie höher, wenn die Federkonstante größer ist. Es gilt:
Umso größer die Federkonstante k, desto höher die Spannenergie ESpann!
Einfluss der Änderung der Ruhelänge auf die Spannenergie
Den Einfluss der Änderung der Ruhelänge auf die Spannenergie kannst du dir mit folgendem Beispiel vorstellen:
- Du hast zwei Federn mit gleicher Dicke am Boden befestigt.
- Jetzt drückst du auf eine Feder einen Ball 2 cm herunter und auf der anderen Feder drückst du ihn 8 cm herunter.
- Du lässt die Bälle los und sie fliegen in die Luft.
Jetzt fliegt der Ball der Feder mit der höheren Änderung der Ruhelänge deutlich höher. Stellst du dir die Spannenergie wieder als Flughöhe des Balls vor, kannst du Folgendes feststellen: Die gespeicherte Spannenergie in der Feder ist höher, wenn die Änderung der Ruhelänge auch höher ist. Es gilt:
Umso größer die Änderung der Ruhelänge x, desto höher die Spannenergie ESpann!
Spannenergie Formel
Die Spannenergie nimmt zu, wenn die Federkonstante und die Änderung der Ruhelänge auch zunehmen. Dazu kannst du auch sagen, die Spannenergie ist direkt proportional zur Federkonstante und Änderung der Ruhelänge.
Wie du in der Formel sehen kannst, hat die Ruhelänge x einen größeren Einfluss auf die Spannenergie, weil sie im Quadrat vorkommt:
Wie jede andere Energieform, kannst du die Spannenergie mit der Einheit Joule oder Nm, also „Newton mal Meter“, angeben. Dabei würde ESpann = 1 J zum Beispiel bedeuten, dass du einen Körper mit einer Federkonstante von 2 
um die Strecke 1 m von ihrer Ruhelänge veränderst.
Natürlich kannst du die Formel der Spannenergie auch nach der Federkonstante oder der Änderung der Ruhelänge umstellen:
| Federkonstante k |  |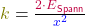
| Änderung der Ruhelänge x |  |
Spannenergie Beispiele
Schauen wir uns ein Beispiel an, wie du die Spannenergie berechnen kannst.
Du hast eine Feder mit einer Federkonstante von 
und änderst ihre Ruhelänge um 3 cm. Wie viel Spannenergie wird dadurch in der Feder gespeichert? Schau dir zunächst die Einheiten an.
Die Federkonstante trägt die Einheit und die Änderung der Ruhelänge cm. Die Spannenergie besitzt als eine Energieform die Einheit Joule (J). Du kannst die Einheit Joule auch als „N • m“ schreiben. Also musst du die 3 cm in 0,03 m umwandeln und alles in deine Formel für die Spannenergie einsetzen:
![\[\textcolor{purple}{E\mathsf{_{Spann}}} = \frac{1}{2} \cdot \textcolor{olive}{k} \cdot \textcolor{blue}{x^2} = \frac{1}{2} \cdot \textcolor{olive}{3000} \ \frac{\text{N}}{\text{m}} \cdot (\textcolor{blue}{0,03} \ \text{m})^2 = \textcolor{purple}{1,35} \ \text{J}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ecf3529edf2041cbe638e7d452eaa0b5_l3.png "Rendered by QuickLaTeX.com")
Anwendungsbeispiel
In welchen Anwendungsgebieten von der Spannenergie Gebrauch gemacht wird, kannst du dir in ein paar Beispielen anschauen!
- Achillessehne: Die Achillessehne wird beim Laufen gestaucht und gedehnt. Sie speichert dabei Spannenergie und reduziert dadurch die Arbeit, die du zum Laufen brauchst.
- Bogenschießen: Beim Bogenschießen wird die Bogensehne gespannt, worin dann die Verformungsenergie gespeichert ist. Beim Loslassen wird sie in die kinetische Energie des Pfeils umgewandelt.
- Radaufhängung: Die Radaufhängung absorbiert beim Auftreffen auf Unebenheiten die Stoßenergie in Form von Spannenergie. Dadurch ist ein gemütliches Fahren trotz Unebenheiten möglich.
Expertenwissen: Spannenergie und Energieerhaltung
Auch die Spannenergie folgt dem Energieerhaltungssatz . Das bedeutet, du kannst die Spannenergie in jede andere Energieform umwandeln. Zum Beispiel in Bewegungsenergie!
Das kannst du dir an einem Beispiel mit der gleichen Feder wie im obigen Zahlenbeispiel anschauen. Mit der Feder soll eine Kugel der Masse 1 kg durch die Gegend befördert werden. Dafür wird die Feder um die Strecke 10 cm zusammengedrückt. Wie schnell wird sich die Kugel dann durch die Luft bewegen? Beim Entspannen der zerdrückten Feder wird die Spannenergie in die kinetische Energie der Kugel umgewandelt. Nach dem Energieerhaltungssatz gilt daher:
![\[E\mathsf{_{Spann \ Feder}} = E\mathsf{_{kin \ Kugel}}.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-34378f369430eea26631ee919091f715_l3.png "Rendered by QuickLaTeX.com")
Mit den entsprechenden Formeln für die Spannenergie und kinetische Energie gilt
![\[\frac{1}{2} \cdot \textcolor{olive}{k} \cdot \textcolor{blue}{x^2} = \frac{1}{2} \cdot m \cdot v^2.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ff0bc3271320914848b30a64fb616360_l3.png "Rendered by QuickLaTeX.com")
Wenn du die Gleichung nach der gesuchten Kugelgeschwindigkeit v umstellst, erhältst du
![\[v = \sqrt{\frac{\textcolor{olive}{k}}{m}} \cdot \textcolor{blue}{x}.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3689c4f02fd18467b622b24e045fe89e_l3.png "Rendered by QuickLaTeX.com")
Nach Einsetzen der Zahlenwerte erhältst du
![\[v = 5,48 \ \frac{\text{m}}{\text{s}}.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-40c35f9a9327d223e0ccaba63001e0f2_l3.png "Rendered by QuickLaTeX.com")
Klasse! Schon hast du die Spannenergie in kinetische Energie umgewandelt! Möchtest du noch mehr über den Energieerhaltungssatz erfahren? Dann schau dir gleich das nächste Video an!
