Fallbeschleunigung
Die Fallbeschleunigung g wird in der Einheit Meter pro Quadratsekunde angegeben. Was sie aussagt und wie du sie berechnest, erfährst du hier und in unserem Video .
Inhaltsübersicht
Fallbeschleunigung einfach erklärt
Fallbeschleunigung nennst du diejenige Beschleunigung, die bei einem freien Fall mit vernachlässigbar kleinem Luftwiderstand auftritt. Auf der Erde beträgt sie durchschnittlich  . Du gibst die Fallbeschleunigung mit dem Formelzeichen
. Du gibst die Fallbeschleunigung mit dem Formelzeichen  an.
an.
Die Fallbeschleunigung gibt an, wie schnell ein Objekt beim freien Fall
seine Geschwindigkeit ändert. An verschiedenen Orten der Erde ist sie unterschiedlich groß. Am Äquator ist sie mit  am kleinsten, während sie an den Polen ganze
am kleinsten, während sie an den Polen ganze  beträgt.
beträgt.
Fallbeschleunigung, Erdbeschleunigung und Ortsfaktor
Sicher ist dir schon einmal der Begriff Erdbeschleunigung begegnet. So nennst du die Fallbeschleunigung auf der Erde. Weitere Synonyme sind Gravitationsbeschleunigung und Schwerebeschleunigung. Auch der Ortsfaktor beschreibt im Grunde dasselbe wie die Fallbeschleunigung. Der Begriff Ortsfaktor betont, dass die Fallbeschleunigung vom Ort abhängt und von Position zu Position unterschiedlich sein kann. Das zeigen die verschiedenen Werte auf der Erde.
- an den Polen auf der Erde:
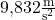
- im Durchschnitt auf der Erde:

- am Äquator auf der Erde:

- 100 km über der Erdoberfläche:

Obwohl der Ortsfaktor meist mit einer anderen Einheit als die Fallbeschleunigung angegeben wird, meint er doch dasselbe. Häufig findest du für den mittleren Ortsfaktor  der Erdoberfläche die Angabe
der Erdoberfläche die Angabe  . Die beiden Einheiten sind aber gleichzusetzen, denn:
. Die beiden Einheiten sind aber gleichzusetzen, denn:
![Rendered by QuickLaTeX.com \[1\frac{\textcolor{magenta}{\si{\newton}}}{\si{\kilogram}}=1\frac{\textcolor{magenta}{\frac{\cancel{\si{\kilogram}}\cdot\colorbox{lime}{\si{\metre}}}{\colorbox{lime}{\si{\s}}^2}}}{\cancel{\si{\kilogram}}}=1\frac{\colorbox{lime}{\si{\metre}}}{\colorbox{lime}{\si{\s}}^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cccc62a21f0b801d2a031051e318fcec_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Fallbeschleunigung berechnen
Erdbeschleunigung
Zur Bestimmung der Erdbeschleunigung gibt es verschiedene Möglichkeiten. Sind Masse und Gewichtskraft eines Körpers an einem Ort bekannt, kannst du die Fallbeschleunigung des Orts mithilfe des zweiten Newtonschen Gesetzes
berechnen. Dabei gilt Fallbeschleunigung  ist Gewichtskraft
ist Gewichtskraft  mal Masse
mal Masse  .
.
![Rendered by QuickLaTeX.com \[g=\frac{F_\mathrm{G}}{m}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-448dcb6a096a41dc7cb1252946a445b7_l3.png)
Auch das Weg-Zeit-Gesetz des freien Falls kannst du nutzen, um die Erdbeschleunigung zu berechnen. Nach der Fallbeschleunigung aufgelöst lautet es: Fallbeschleunigung  ist zwei mal die Fallstrecke
ist zwei mal die Fallstrecke  geteilt durch das Quadrat der Fallzeit
geteilt durch das Quadrat der Fallzeit  . Mithilfe eines geeigneten Versuchs lassen sich Fallstrecke und Fallzeit eines Objekts messen und so die Erdbeschleunigung bestimmen.
. Mithilfe eines geeigneten Versuchs lassen sich Fallstrecke und Fallzeit eines Objekts messen und so die Erdbeschleunigung bestimmen.
![Rendered by QuickLaTeX.com \[g=\frac{2\cdot{s}}{t^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b32f03900d85e17126c846860e73b330_l3.png)
Eine weitere Möglichkeit, die Fallbeschleunigung experimentell zu bestimmen, bietet das Fadenpendel. Für kleine Auslenkungen berechnest du seine Schwingungsdauer mit folgender Formel:
![Rendered by QuickLaTeX.com \[T=2\pi\cdot\sqrt{\frac{l}{g}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fa08ff6cee760e01f48862ab87cba6c8_l3.png)
Die Schwingungsdauer  und die Fadenlänge
und die Fadenlänge  können im Versuch gemessen werden. Das Umstellen der Formel nach
können im Versuch gemessen werden. Das Umstellen der Formel nach  liefert dann:
liefert dann:
![Rendered by QuickLaTeX.com \[g=\frac{4\pi^2\cdot{l}}{T^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d66e7f573ee315f07d7827b8bd5814d_l3.png)
Fallbeschleunigung der Himmelskörper
Aber nicht nur auf der Erde gibt es eine Fallbeschleunigung. Alle größeren Himmelskörper verfügen über eine messbare Gravitationskraft, mit der sie Massen beschleunigen können. Für die Berechnung der Beschleunigung verwendest du das zweite Newtonsche Gesetz (1) und das Gravitationsgesetz (2).
![Rendered by QuickLaTeX.com \[\begin{flushleft} \left(1\right)\hspace{10mm}{F=m_\mathrm{K}\cdot{g}}\\ \left(2\right)\hspace{10mm}{F_\mathrm{G}=G\cdot\frac{m_\mathrm{H}\cdot{m_\mathrm{K}}}{r^2}} \end{flushleft}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-001db8cf38c9cee2a6032fd304ccb8d5_l3.png)
Die Massen  und
und  entsprechen dabei den Massen des Himmelskörpers und des von ihm angezogenen Körpers. Die Gravitationskonstante
entsprechen dabei den Massen des Himmelskörpers und des von ihm angezogenen Körpers. Die Gravitationskonstante  ist eine fundamentale Naturkonstante und beträgt ungefähr
ist eine fundamentale Naturkonstante und beträgt ungefähr  . Da die Kraft
. Da die Kraft  des Newtonschen Gesetzes in dem Fall der Gewichtskraft
des Newtonschen Gesetzes in dem Fall der Gewichtskraft  entspricht, können sie gleichgesetzt und nach der Fallbeschleunigung
entspricht, können sie gleichgesetzt und nach der Fallbeschleunigung  aufgelöst werden:
aufgelöst werden:

Mithilfe der Formel ‚Fallbeschleunigung  ist Gravitationskonstante
ist Gravitationskonstante
 mal Masse
mal Masse  geteilt durch Radius
geteilt durch Radius  zum Quadrat‘ lässt sich nun die Fallbeschleunigung auf der Oberfläche jedes Himmelskörpers bestimmen.
zum Quadrat‘ lässt sich nun die Fallbeschleunigung auf der Oberfläche jedes Himmelskörpers bestimmen.
Fallbeschleunigung Beispiele
Die Fallbeschleunigung hängt also von dem Radius und der Masse der Himmelskörper ab. Je kleiner und schwerer sie sind, desto größer ist die Fallbeschleunigung. Das kannst du auch an folgenden Beispielen erkennen:
| Himmelskörper | Fallbeschleunigung | Masse | Radius |
| Erde |  |
 |
 |
| Mond | 
|
 |
 |
| Mars | 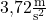
|
 |
 |
| Jupiter | 
|
 |
 |
| Sonne | 
|
 |
 |
Wie du die Werte der Tabelle nutzt, um die Geschwindigkeit eines freien Falls auf den Himmelskörpern zu berechnen, erfährst du in unserem Video dazu!
