Kräfteparallelogramm
Gemäß eines mechanischen Gesetzes dürfen Kräfte addiert oder zerlegt werden. Doch wie genau geht man hierbei vor? Ganz einfach – mit dem Kräfteparallelogramm! In diesem Artikel wird das Kräfteparallelogramm näher betrachtet und gezeigt, wie man mit dessen Hilfe eine Kräfteaddition bzw. -zerlegung durchführt.
Du bist eher der audiovisuelle Lerntyp ? Kein Problem! Unser Video erklärt dir alles was du dazu wissen musst.
Inhaltsübersicht
Kräfteparallelogramm einfach erklärt
Das Kräfteparallelogramm ist ein Instrument zur geometrischen Ermittlung von Kräften. Grundlegend hierfür ist folgende Gesetzgebung aus der Mechanik: Je zwei am selben Punkt angreifende Kräfte können durch eine einzige Kraft ersetzt werden. Aus mathematischer Sicht entspricht dieser Ablauf einer Vektoraddition. Die Umkehrung des Vorgehens wird Kräftezerlegung genannt.
Diese resultierende Kraft wird auch Gesamt– oder Ersatzkraft genannt. Sie hat die gleiche Wirkung auf den Körper wie beide Ausgangskräfte.
Kräfteparallelogramm zeichnen
Um das Kräfteparallelogramm nun zu zeichnen, zeichnet man zunächst beide Ausgangkraftvektoren mit ihrem Betrag und Richtung.
Daraus ergibt sich ein Parallelogramm. Die Diagonale des Parallelogramms entspricht dabei der Ersatzkraft. Liegen die beiden Vektoren nicht auf einem Angriffspunkt können sie entlang ihrer Wirkungslinien verschoben werden, bis dies der Fall ist.
Mathematisch gesehen entspricht dies der Vektoraddition beider Kraftvektoren. Wenn die Wirkungsrichtung der Kraftvektoren bekannt ist, kann der Betrag der Gesamtkraft bestimmt werden. Dreht man den Prozess um, hat man die Kräftezerlegung.
Das Gesetz des Kräfteparallelogramms kann nicht durch andere Gesetze, zum Beispiel die newtonsche Gesetze, bewiesen werden. Das bedeute es hat einen axiomatischen Charakter. Es wird allerdings durch die Praxis als bestätigt angesehen.
Erweitert man das Konzept auf mehr als zwei angreifende Kräfte, spricht man von einem Kräfteeck. Allerdings kann für das Zusammenfassen von mehr als zwei Kräften auch das Kräfteparallelogramm eingesetzt werden. Dazu werden zunächst zwei Kräfte zu einem resultierenden Kraftvektor zusammengefasst und anschließend die Resultierende wieder mit weiteren Kräften.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kräfteaddition mit dem Kräfteparallelogramm
Bei der Kräfteaddition wirken zwei Kräfte auf einen starren Körper. Nun kann die resultierende Kraft grafisch ermittelt werden. Dazu werden erst die Kräfte in ihrem Angriffspunkt mit richtigem Betrag und Richtung angezeichnet.
Anschließend verschiebt man die Pfeile in Richtung eines gemeinsamen Angriffspunktes. Dabei wird den Wirkungslinie der Kraftvektoren gefolgt.
Um das Parallelogramm zu erhalten werden die Vektoren dupliziert und parallel entlang der jeweils anderen Wirkungslinie, bis zur Spitze des anderen Vektors, verschoben. Nun haben wir unser Parallelogramm und können die Resultierende als Diagonale einzeichnen.
Aufgabe: Addition zweier Kräfte
Die Kräfte  und
und  greifen in einem gemeinsamen Angriffspunkt an. Die Kräfte müssen also nicht mehr verschoben werden.
greifen in einem gemeinsamen Angriffspunkt an. Die Kräfte müssen also nicht mehr verschoben werden.
Der Winkel ist mit  bekannt. Die Kraft
bekannt. Die Kraft  beträgt 15 Newton und die Kraft
beträgt 15 Newton und die Kraft  beträgt 40 Newton. Nun wird die Formel für
beträgt 40 Newton. Nun wird die Formel für  aufgestellt. Dazu bedienen wir uns dem Cosinus-Satz. a entspricht dabei der resultierenden Kraft
aufgestellt. Dazu bedienen wir uns dem Cosinus-Satz. a entspricht dabei der resultierenden Kraft  , b dem Vektor
, b dem Vektor  und c dem Vektor
und c dem Vektor  .
.


Nach dem Einsetzten der Werte ergibt sich für die Gesamtkraft 52,4 Newton.

Übung: Addition dreier Kräfte
Bei der Addition mehrerer Kräfte müssen zunächst die einzelnen Teilkräfte in ihre x und y Komponenten zerlegt werden. Anschließend werden die Teilresultierenden  und
und  in x und in y-Richtung berechnet. Davon kann dann auch auf die Gesamtresultierende geschlossen werden.
in x und in y-Richtung berechnet. Davon kann dann auch auf die Gesamtresultierende geschlossen werden.
In diesem Beispiel haben wir drei Kräfte  ,
,  und
und  , ihre Beträge und ihre Richtung. Es wird mit den Komponenten in x-Richtung begonnen.
, ihre Beträge und ihre Richtung. Es wird mit den Komponenten in x-Richtung begonnen.



Daraus kann die Resultierende für die x-Richtung bestimmt werden:

Als nächstes werden die Komponenten in y-Richtung betrachtet.



Die Resultierende in y-Richtung ist:

Mit den beiden Resultierenden in x- und y-Richtung kann nun die Gesamtresultierende berechnet werden.

Nun fehlt noch die Richtung der Resultierenden. Die Berechnung erfolgt mit dem Tangens der Teilresultierenden.


Auf den Winkel müssen noch 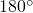 aufaddiert werden, da y positiv und x negativ sein muss.
aufaddiert werden, da y positiv und x negativ sein muss.

Kräftezerlegung mit dem Kräfteparallelogramm
Haben wir nur eine Kraft und wollen diese genauer betrachten, können wir sie in zwei Teilkräfte aufspalten. Diese müssen sich im selben Punkt schneiden. Dazu muss zuerst die Wirkungslinie der beiden Teilkräfte festgelegt werden. Nun kann der Betrag der Teilkräfte ermittelt werden. Zunächst werden dazu wieder die Ausgangskraft und die beiden gewünschten Wirkungslinien aufgezeichnet. Falls die Resultierende noch nicht auf dem Wirkungslinien-Schnittpunkt liegt muss sie nun auf diesen verschoben werden.
Grundsätzlich bietet es sich natürlich an die Wirkungslinie so zu wählen, dass der Angriffspunkt der Gesamtkraft bereits darauf liegt. Anschließend dupliziert und verschiebt man die Wirkungslinien der Teilkräfte parallel, so dass sie die Spitze der Resultierenden berühren. Nun haben wir wieder ein Parallelogramm.
Die Kanten des Parallelogramms bis zum Schnittpunkt entsprechen den Kraftvektoren der Teilkräften.
Aufgabe: Zerlegung einer Kraft
Auch hier sehen wir uns wieder eine Aufgabe an. Die Kraft  hat 60 Newton und wirkt unter einem Winkel
hat 60 Newton und wirkt unter einem Winkel  von
von  . Nun soll diese in eine y- und in eine x-Komponente zerlegt werden, gemäß dem Koordinatensystem. Zunächst werden nun die Wirkungslinien und dann das Parallelogramm gezeichnet.
. Nun soll diese in eine y- und in eine x-Komponente zerlegt werden, gemäß dem Koordinatensystem. Zunächst werden nun die Wirkungslinien und dann das Parallelogramm gezeichnet.
Hier können wir mit den Dreiecksformeln arbeiten. Falls kein rechter Winkel vorhanden sein sollte, wird alternativ mit dem Cosinus-Satz gerechnet. Für die Kraft in x-Richtung ergibt sich:

Und für den Kräftevektor in y-Richtung:
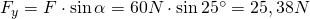
Übung: Kräfteparallelogramm an der schiefen Ebene
Ein typisches Anwendungsbeispiel des Kräfteparallelogramms ist die schiefe Ebene.
Es wird angenommen, dass ein Kasten Bier eine schiefe Ebene unter einem Winkel von  herunterrutscht. Auf diesen wirkt nun senkrecht zum Erdmittelpunkt die Gewichtskraft
herunterrutscht. Auf diesen wirkt nun senkrecht zum Erdmittelpunkt die Gewichtskraft  . Außerdem hat man senkrecht zur schiefen Ebene die Normalkraft
. Außerdem hat man senkrecht zur schiefen Ebene die Normalkraft  . Diese drückt den Kasten an die schiefe Ebene, die genaue Größe ist allerdings nicht bekannt. Des Weiteren haben wir eine Hangabtriebskraft
. Diese drückt den Kasten an die schiefe Ebene, die genaue Größe ist allerdings nicht bekannt. Des Weiteren haben wir eine Hangabtriebskraft  parallel zur schiefen Ebene. Auch hier ist die genaue Größe nicht bekannt, deshalb zeichnen wir für
parallel zur schiefen Ebene. Auch hier ist die genaue Größe nicht bekannt, deshalb zeichnen wir für  und
und  zunächst nur Wirklinien ein. Nun können wir das Kräfteparallelogramm mit Hilfe von
zunächst nur Wirklinien ein. Nun können wir das Kräfteparallelogramm mit Hilfe von  einzeichnen.
einzeichnen.  entspricht nämlich der Resultierenden beider Kräfte.
entspricht nämlich der Resultierenden beider Kräfte.
Nun wollen wir die Normal– und die Hangabtriebskraft berechnen. Nehmen wir an, der Kasten wiegt 18 kg. Dies ergibt eine Gewichtskraft von:

Nun soll die Kraft aufgeteilt werden.
Die Normalkraft lässt sich mit Hilfe des Cosinus berechnen.

Für die Hangabtriebskraft wird hingegen der Sinus verwendet.

Kräfteparallelogramm paralleler Kräfte
Ein besonders einfacher Fall ist das Kräfteparallelogramm bei parallel wirkenden Kräften. Hier werden die Kräfte aufaddiert, wenn sie in die gleiche Richtung wirken. Oder sie werden von einander subtrahiert, wenn sie in entgegengesetzte Richtung wirken.


