Normalkraft und Hangabtriebskraft
Die Normalkraft und Hangabtriebskraft sind Begriffe, denen du mit Sicherheit schon einmal begegnet bist. In diesem Beitrag erfährst du was diese Kräfte sind und welche Formeln es gibt.
In unserem Video zur Normalkraft und Hangabtriebskraft findest du Erklärungen mit Bild und Ton dargestellt, sodass du das Thema noch schneller verstehen kannst.
Inhaltsübersicht
Normalkraft einfach erklärt
Nimm dir einen Würfel und stelle ihn auf den Tisch. Was wirst du beobachten? Nichts. Der Würfel wird ruhig auf dem Tisch liegen und es wird nichts passieren. Aber auf den Würfel wirkt die Gravitationskraft und nach Newton folgt aus einer resultierenden Kraft eine Beschleunigung.
Wie kann also der Würfel ruhig auf dem Tisch liegen? Die Antwort: Eine weitere Kraft muss die Gravitationskraft ausgleichen. Und genau diese Kraft heißt Normalkraft.
Bei der Normalkraft handelt es sich um eine Kontaktkraft, die verhindert, dass ein Festkörper durch einen anderen Festkörper hindurchtreten kann. Die Richtung der Normalkraft ist immer entgegengesetzt zu der senkrechten Komponente der Gravitationskraft, die auf eine Oberfläche wirkt.
Befinden sich zwei Körper nicht im Kontakt, kann der eine Körper auf den anderen Körper auch keine Normalkraft ausüben.
Normalkraft Formel
Die Normalkraft gleicht also die senkrechte Komponente der Gravitationskraft aus. In typischen Problemstellungen in der Physik musst du daher zunächst die senkrechte Komponente herausfinden, um auf die Normalkraft zu kommen. In diesem Abschnitt schauen wir uns die beiden prototypischen Beispiele einer waagerechten und einer schiefen Ebene an und wie du auf die Formel für die Normalkraft in beiden Fällen kommen kannst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Normalkraft waagerechte Ebene
Kehren wir zurück zu unserem Würfel auf dem Tisch. Der Tisch stellt dabei eine waagerechte Ebene dar. Vergiss zunächst einmal, dass der Tisch überhaupt da ist. Welche Kräfte wirken dann auf den Würfel?
Der Würfel besitzt eine konkrete Masse  . Damit reagiert er auf die Gravitation der Erde. Er erfährt eine nach unten gerichtete Gewichtskraft
. Damit reagiert er auf die Gravitation der Erde. Er erfährt eine nach unten gerichtete Gewichtskraft
 mit dem Betrag
mit dem Betrag
 ,
,
wobei  die Schwerebeschleunigung in der Nähe der Erdoberfläche ist. Können andere Kräfte auf den Würfel wirken? Der Würfel ist elektrisch neutral. Daher kann er auf keine elektrische
oder magnetische
Felder reagieren. Die anderen beiden fehlenden Kräfte – die starke
und die schwache Wechselwirkung
– befinden sich außerhalb des Rahmens dieses Artikels. Zumindest können wir dir sagen, dass auch diese beiden Kräft auf den Würfel nicht wirken.
die Schwerebeschleunigung in der Nähe der Erdoberfläche ist. Können andere Kräfte auf den Würfel wirken? Der Würfel ist elektrisch neutral. Daher kann er auf keine elektrische
oder magnetische
Felder reagieren. Die anderen beiden fehlenden Kräfte – die starke
und die schwache Wechselwirkung
– befinden sich außerhalb des Rahmens dieses Artikels. Zumindest können wir dir sagen, dass auch diese beiden Kräft auf den Würfel nicht wirken.
Damit ist die Gravitationskraft die einzige Kraft, die auf den Würfel wirkt. Wäre der Tisch nicht da, würde der Würfel deshalb nach unten beschleunigt werden. Der Tisch ist aber da, weshalb sich der Würfel nicht bewegt. Folglich muss der Tisch auf den Würfel eine Kraft ausüben, die der Gravitationskraft entgegengesetzt ist. Diese Kraft bekommt den Namen Normalkraft und hat den Betrag
Normalkraft waagerechte Ebene: 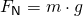
und die Richtung
Richtung Normalkraft waagerechte Ebene: In die zur Gravitationskraft entgegengesetzte Richtung.
Die Normalkraft auf der waagerechten Ebene muss diese beiden Kriterien erfüllen, denn nur dann ist die resultierende Kraft auf den Würfel gleich Null.
Beispiel
Schauen wir uns doch ein Beispiel dazu an. Hierfür nehme wir an, dass die Masse des Würfels 4 kg ist. Die Schwerebeschleunigung hat den Wert 9,81. Für die auf den Würfel wirkende Gravitationskraft gilt dann
 .
.
Da der Würfel auf dem Tisch ruht, muss die resultierende Kraft auf den Würfel gleich Null sein. Die zur Gravitationskraft entgegengesetzte Normalkraft ergibt sich dann zu
 .
.
Wenn also die Erde auf den Würfel eine Gravitationskraft von 39,24 N in Richtung Boden ausübt, so übt der Tisch auf den Würfel eine Normalkraft von exakt 39,24 N in Richtung Himmel aus. Nur dann bleibt der Würfel in Ruhe.
Normalkraft schiefe Ebene
Nun sind nicht alle Ebenen waagerecht. Die Situation für schiefe Ebenen unterscheidet sich aber von der Situation einer waagerechte Ebene nur im Winkel der schiefen Ebene relativ zum Boden. Egal ob schief oder waagerecht, die Normalkraft gleicht die senkrechte Komponente der Gravitationskraft aus. Mehr tut sie nicht.
Was bedeutet das konkret? Du musst also irgendwie auch bei der schiefen Eben die senkrechte Komponente bestimmen. Anders als bei der waagerechten Ebene ist die senkrechte Komponente bei der schiefen Ebene aber nicht gleich der Gravitationskraft  selber. Diese wirkt stets in Richtung Boden.
selber. Diese wirkt stets in Richtung Boden.
Für die waagerechte Ebene hatten wir Glück, denn „Richtung Boden“ und „senkrecht zum Tisch“ waren identische Richtungen. Bei der schiefen Ebene ist das leider nicht der Fall. Wenn wir den Winkel relativ zum Boden mit  bezeichnen, dann ergibt sich die senkrechte Komponente der Gravitationskraft zu
bezeichnen, dann ergibt sich die senkrechte Komponente der Gravitationskraft zu

und genau diesen Betrag aber die entgegengesetzte Richtung besitzt die Normalkraft. Es gilt also
Normalkraft schiefe Ebene:  .
.
Zwei Sachen solltest du dir an dieser Stelle merken. Erstens meint „senkrecht“ immer senkrecht zur Oberfläche, wo die zwei Körper in Kontakt stehen. Zweitens zeigt die Normalkraft immer entgegengesetzt zur senkrechten Komponente der Gravitationskraft, besitzt aber den exakt gleichen Betrag.
Du findest häufig die Normalkraft nur im Zusammenhang mit der schiefen Ebene. Die Existenz der Normalkraft ist aber nicht davon abhängig, ob die Ebene nun schief ist oder nicht. In der Tat haben wir dir gezeigt, dass auch bei der waagerechten Ebene eine Normalkraft wirken muss. Die charakterisierenden Eigenschaften der Normalkraft bleiben dieselben, egal wie schief die Ebene nun sein mag.
Beispiel
Lass uns auch hierzu ein kleines Beispiel rechnen. Nehmen wir dazu die Situation von vorhin, neigen aber den Tisch relativ zum Boden um den Winkel 10°. Wie groß ist die Normalkraft in diesem Fall?
Dazu nehmen wir die Formel

her und setzen unsere Werte ein. Wir erhalten
 .
.
Wenn du dich dafür interessierst, woher die Formel kommt, und weitere Beispiele sehen möchtest, dann schaue bei unserem ausführlichen Beitrag zur schiefen Ebene vorbei.
Hangabtriebskraft einfach erklärt
Nehmen wir wieder unseren Würfel auf den Tisch her. Diesmal ist aber der Tisch so geneigt, dass der Würfel beginnt, sich entlang des Tisches zu bewegen. Nach Newton wissen wir, dass dann auf dem Würfel eine resultierende Kraft wirken muss.
Die Hangabtriebskraft ist die Kraft, die einen Körper entlang einer schiefen Ebene in Bewegung setzt. Die Richtung der Hangabtriebskraft ist immer parallel zur schiefen Ebene und zeigt in Bewegungsrichtung. Ihr Betrag ist gerade die zur schiefen Ebene parallele Komponente der Gravitationskraft, die auf dem Körper wirkt.
Hangabtriebskraft ohne Reibung
Der Betrag der Hangabtriebskraft entspricht der zur schiefen Ebene parallelen Komponente der Gravitationskraft. Es gilt daher
Betrag Hangabtriebskraft: 
und
Richtung Hangabtriebskraft: Parallel zur schiefen Ebene in Bewegungsrichtung.
Wie bei der Normalkraft ist  der Winkel der schiefen Ebene relativ zum Boden. Anders als bei der Normalkraft, kann von der Hangabtriebskraft nur im Zusammenhang mit der schiefen Ebene gesprochen werden.
der Winkel der schiefen Ebene relativ zum Boden. Anders als bei der Normalkraft, kann von der Hangabtriebskraft nur im Zusammenhang mit der schiefen Ebene gesprochen werden.
Beispiel
Für das Beispiel von vorhin mit dem 4 kg schweren Würfel auf dem um 10° geneigten Tisch ergibt sich die Hangabtriebskraft zu
 .
.
Ohne weitere Kräfte wird diese Hangabtriebskraft von 6,81 N den Würfel parallel zur Oberfläche des geneigten Tisches in Bewegung setzen. Das keine weiteren Kräfte auf den Würfel wirken, ist aber nur der Idealfall. Tatsächlich wirkt aber eine weitere Kraft auf den Würfel, die sogenannte Reibungskraft . Erst nachdem die Hangabtriebskraft diese „bewegungshemmende“ überwunden hat, bewegt sich der Würfel. Wie das funktioniert, schauen wir uns im nächsten Unterabschnitt an.
Hangabtriebskraft mit Reibung
Egal wie glatt zwei Flächen zu scheinen mögen, zwischen ihnen kommt es stets zur Reibung . Auch zwischen unserem Würfel und dem geneigten Tisch kommt es zur Reibung. Wollen wir nun die Reibungskraft ausrechnen, die dadurch auf den Würfel wirkt, benötigen wir eine weitere Zahl, die die Reibung makroskopisch beschreibt. Diese Zahl heißt Reibungskoeffizient und ermöglicht das Berechnen von Reibungskräften.
Beispiel
Wie aber sieht ein typisches Beispiel dafür aus? Der Reibungskoeffizient ist immer bezüglich zwei Oberflächen definiert. Nehmen wir also an, dass der Reibungskoeffizient zwischen Würfeloberfläche und Tischoberfläche gerade 0,2 ist.
Die Reibungskraft, die von der Hangabtriebskraft überwunden werden muss, ergibt sich zu
 .
.
Hier ist  das häufig benutzte Symbol für den Reibungskoeffizienten und
das häufig benutzte Symbol für den Reibungskoeffizienten und 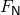 ist die Normalkraft auf der schiefen Ebene, die wir vorhin besprochen haben. Setzen wir die gegebenen Werte ein, bekommen wir
ist die Normalkraft auf der schiefen Ebene, die wir vorhin besprochen haben. Setzen wir die gegebenen Werte ein, bekommen wir
 .
.
Wir hatten zuvor für die Hangabtriebskraft den Wert  . Es gilt also
. Es gilt also
 .
.
Somit überwiegt die Reibungskraft die Hangabtriebskraft und folglich schafft es die Hangabtriebskraft nicht den Würfel in Bewegung zu setzen.
Normalkraft und Hangabtriebskraft in der schiefen Ebene
Zum Abschluss geben wir dir eine Gesamtübersicht, wie die Normalkraft und die Hangabtriebskraft sowie die damit zusammenhängenden Kraft in einer schiefen Ebene wirken.
Du kannst dir gerne wieder den ruhenden Würfel auf dem geneigten Tisch vorstellen. Auf ihm wirkt die Gravitationskraft, die Richtung Boden zeigt. Diese Gravitationskraft lässt sich in eine Komponente senkrecht zur Tischoberfläche und in einer parallel dazu aufteilen. Die parallele Komponente ist die Hangabtriebskraft und versucht den Würfel in Bewegung zu setzen. Dieser Komponente wirkt die Reibungskraft entgegen, die im Fall des ruhenden Würfels größer oder gleich zur Hangabtriebskraft ist. Die Reibungskraft zeigt demnach entgegengesetzt zur Hangabtriebskraft. Der Würfel bewegt sich auch nicht senkrecht zur Tischoberfläche. Daher muss eine zur senkrechten Komponente der Gravitationskraft entgegengesetzte Normalkraft wirken.
Wieso darfst du aber überhaupt die Gravitationskraft in einer Komponente parallel und einer Komponente senkrecht zur schiefen Ebene zerlegen? Diese Kräftezerlegung beruht auf dem Prinzip der Superposition . Wenn du mehr darüber erfahren möchtest, dann klicke doch einfach auf die Verlinkungen. Diese führen dich zu zwei ausführlichen Beiträgen (inklusive Video), die diese beiden Themen behandeln.
Zusammengefasst solltest du dir folgendes merken: Die Normalkraft zeigt entgegengesetzt zur senkrechten Komponente der Gravitationskraft. Ihr Betrag entspricht gerade dem Betrag dieser senkrechten Komponente. Die Hangabtriebskraft ist die zur schiefen Ebene parallele Komponente der Gewichtskraft. Während die Normalkraft also eine „neue Form“ von Kraft ist, ist die Hangabtriebskraft nur die parallele Komponente der Gewichtskraft.
Beachte, dass häufig die Normalkraft mit der senkrechten Komponente der Gewichtskraft gleichgesetzt wird. Ihr Betrag mag zwar der gleiche sein, es handelt sich aber um zwei unterschiedliche Kräfte. In solchen (falschen) Darstellungen wird dann die Normalkraft in Richtung der senkrechten Komponente gezeichnet.

