Massenträgheitsmoment
In diesem Videobeitrag behandeln wir das Massenträgheitsmoment. Dafür definieren wir zuerst das Trägheitsmoment und zeigen dir daraufhin, wie du es berechnen kannst. Danach gehen wir auf einige Massenträgheits-Formeln ein, die wir in einer Tabelle zusammengefasst haben.
Unser Video erspart es dir den Text zu lesen und erklärt dir alles in kürzester Zeit. Außerdem behandeln wir dort auch die Formeln einer Punktmasse, eines Stabes, eines Zylinder und einer Kugel. Schau doch rein!
Massenträgheitsmoment Definition
Das Massenträgheitsmoment spiegelt den Widerstand eines Körpers gegen eine Änderung seiner Drehbewegung wider. Es wird auch oft als Inertialmoment oder nur als Trägheitsmoment bezeichnet. Die Verallgemeinerung des Moments ist der sogenannte Trägheitstensor.
Das Massenträgheitsmoment kann mit der Masse bei der translatorischen Bewegung, welche sich aus Kraft geteilt durch Beschleunigung ergibt, verglichen werden. Die Kraft bei einer geradlinigen Bewegung ergibt sich nämlich aus der Masse 
und der Beschleunigung 
.
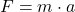
Das Drehmoment
berechnet sich aus dem Trägheitsmoment 
und der Winkelbeschleunigung
.
Daran kannst du die Analogie der Masse und des Massenträgheitsmoment sehr gut erkennen.
Wenn du mehr zu Kraft, Beschleunigung und in diesem Zusammenhang, den Newtonschen Axiomen wissen möchtest, haben wir dir hier die jeweiligen Videos verlinkt. Das Trägheitsmoment wird einerseits für Flächen und andererseits für Massen formuliert. Für das Flächenträgheitsmoment haben wir einen extra Beitrag sowie ein Video erstellt. In diesem Artikel zum Massenträgheitsmoment betrachten wir ausschließlich die Rotation einer Masse um eine Drehachse.
Massenträgheitsmoment Formel
Das Trägheitsmoment ist abhängig von der Massenverteilung eines Körpers bezüglich der jeweiligen Drehachse. So musst du das Volumenintegral über die Massenverteilung 
eines Körpers berechnen. Die Massenverteilung ist mit anderen Worten nichts anderes als die Dichte, die abhängig vom Ortsvektor ist.
Bei dieser Formel ist 
das Volumen und 
ist der zur Rotationsachse senkrechte Anteil von dem Radius 
zu dem jeweiligen betrachteten Volumenelement. Genauso kann statt über das Volumen, auch über die Masse 
integriert werden.
Massenträgheitsmoment Punktmasse
Das Integral für das Inertialmoment lässt sich im Falle einer rotieren Punktmasse vereinfachen .
Die Masse des Massenpunktes ist und 
der Abstand des Punktes von der Drehachse, was nichts anderes als der Radius ist. Im Falle von mehreren angegeben Punkten, kannst du die Formel über diese aufsummieren. Das ist möglich, da Trägheitsmomente, die sich auf dieselbe Rotationsachse beziehen aufaddiert werden können.
Rotation um Symmetrieachse
Im Nachfolgenden werden nur rotationssymmmetrische Körper betrachtet, die um eine ihrer Symmetrieachsen rotieren. Falls dies der Fall ist, kann das Massenträgheitsmoment mit der Hilfe von Zylinderkoordinaten bestimmt werden. Auch zu diesen Koordinaten findest du alle Informationen in unserem zugehörigen Beitrag. Die Rotationsachse wird hierbei als z-Achse bezeichnet. Im nächsten Schritt muss das Volumenintegral an die Koordinaten angepasst werden. Das Volumenelement ergibt nun:
Mit der Annahme, dass es sich um einen Körper mit homogener Massenverteilung handelt, kannst du das 
noch als Konstante vor das Integral ziehen. So kommt es zu einem Dreifach-Integral:
Aufgepasst werden muss in diesem Fall auf die Definition von . Das große 
ist der Radius und dient als Integrationsgrenze. Das kleine ist der Abstand zwischen dem Massenelement und der Drehachse. Auch musst du die Abnahme des Zylinders hin zu seiner Spitze berücksichtigen. Hier muss dir entweder die Höhe als Funktion des Radius oder der Radius als Funktion der z-Achse bekannt sein. Ansonsten kannst du das Integral nicht lösen.
Massenträgheitsmomente relevanter Körper
Im Folgenden stellen wir dir wichtige geometrische Körper und ihre jeweiligen Formeln vor. Typisch dabei ist, dass die Objekte um eine ihrer Symmetrieachsen rotieren. Aufgrund dessen können die Zylinderkoordinaten verwendet werden.
Massenträgheitsmoment Stab
Falls ein dünner Stab um seine Symmetrieachse rotiert, ergibt sich das Trägheitsmoment zu:
Die Masse des Stabes ist und 
ist die Länge.
Massenträgheitsmoment Zylinder
Die Formel für das Trägheitsmoment eines Zylinders, der wieder um seine Symmetrieachse rotiert, kann wie folgt geschrieben werden:
Der Abstand von der Drehachse zu der Außenseite des Zylinders wird mit dem Formelzeichen beschrieben.
Massenträgheitsmoment Hohlzylinder
Es gibt verschiedene Variationen eines Zylinders. Eine davon ist der Hohlzylinder. Die Besonderheit ist hier, dass zwei Radien in die Formel mit einfließen. Einmal der Radius von der Drehachse zur Außenseite des Zylinders 
und zum Anderen der Abstand von der Achse hin zur Innenseite des Zylinders 
.
In einem Bild sieht es dann wie folgt aus:
Massenträgheitsmoment Kugel
Eine Vollkugel, die um eine Achse rotiert, die durch ihren Mittelpunkt geht, hat folgendes Massenträgheitsmoment:
Im Falle einer Kugel und genau dieser Position der Rotationsachse, ist der Radius der Kugel.
Massenträgheitsmoment Quader
Der letzte wichtige Körper ist der Quader. Dieser rotiert um eine Achse durch den Mittelpunkt. Die Formel ergibt sich dann zu:
Die Seitenlängen sind dabei und 
. In dem Bild findest du die genaue Benennung.
Massenträgheitsmoment Einheit
Meistens wird das Massenträgheitsmoment mit dem Formelzeichen 
oder bezeichnet. Wir gebrauchen in diesem Artikel das Zeichen . Da das Trägheitsmoment durch Masse mal Radius im Quadrat definiert ist, ergibt sich die Einheit zu 
.
Massenträgheitsmoment berechnen
Wie du oben gesehen hast, ist die Masse und die Rotationsachse der Bewegung des starren Körpers wichtig. Nun kann die Verteilung der Masse innerhalb eines Körpers gleichbleiben oder die Rotationsachse entspricht keiner Symmetrieachse. Im Folgenden findest du Formeln, wie du mit diesen Fällen umgehst.
Homogene Massenverteilung
Der erste Sonderfall ist, wenn der betrachtete Körper eine homogene Massenverteilung hat. Das bedeutet es gibt keine Unregelmäßigkeiten. So wäre die Massenverteilung keine Funktion mehr, sondern eine Konstante und du kannst sie aus dem Integral herausziehen. Die Formel für das Trägheitsmoment mit einer homogenen Massenverteilung ist:
Trägheitsmoment und Steinerscher Satz
Zum Steinerschen Satz haben wir ebenfalls ein Video und einen Beitrag für dich erstellt.
Kurz zusammengefasst geht es beim Steinerschen Satz um die Verschiebung der Rotationsachse innerhalb eines Körpers. Wenn das Massenträgheitsmoment für eine Drehachse durch den Schwerpunkt des Körpers 
bekannt ist, kannst du dieses mit folgender Formel für jede andere Achse 
bestimmen.
Dabei ist 
der Abstand der Drehachse des Schwerpunktes zu der verschobenen Achse.
Massenträgheitsmoment Tabelle
Im Folgenden sollen die wichtigsten Formeln für Massenträgheitsmomente zusammengefasst werden. Dabei haben wir dir das Massenträgheitsmoment einer Punktmasse, eines Quaders, eines dünnen Stabes, des Vollzylinders, eines Hohlzylinders, einer Vollkugel und des Kegels zusammengefasst. Alle Körper rotieren dabei um ihre jeweilige Symmetrieachse.
