Corioliskraft berechnen
In diesem Artikel lernst du was die Corioliskraft ist und wie sie in unserem Alltag mitwirkt. Außerdem zeigen wir dir ein Beispiel, wie du die Corioliskraft mathematisch herleiten und berechnen kannst.
Für den maximalen Lernerfolg haben wir das Thema für dich audiovisuell aufbereitet. Schau dir daher am besten noch unser Video zur Corioliskraft an.
Inhaltsübersicht
Corioliskraft einfach erklärt
Die Corioliskraft ist eine Scheinkraft, deren Wirkung auf Körper innerhalb rotierender Bezugssysteme beobachtet wird. Ein solches Bezugssystem kann zum Beispiel eine Drehscheibe sein, über die du einen Ball rollen lässt.
Stell dir hierzu vor, dass du in der Mitte einer rotierenden Scheibe stehst. Du willst einen Ball zum dir gegenüberliegenden Rand der Scheibe rollen lassen. Dabei stellst du fest, dass sich der Ball nicht gemäß dem zweiten newtonschen Gesetz bewegt. Für dich, als auf der Drehscheibe befindlichen Beobachter, scheint es, als ob der Ball senkrecht zu seiner Bewegungsrichtung beschleunigt wird. Damit wird seine gradlinige Bewegung, seitlich abgelenkt. Diese Beschleunigung bezeichnet man auch als Coriolisbeschleunigung.
Die Corioliskraft wird als Scheinkraft bezeichnet, da sie nur in Zusammenhang mit einer Beschleunigungskraft auftritt.
Wie du dir sicher schon denken kannst, sieht ein Außenstehender Beobachter den Ball geradlinig auf den Rand zurollen und somit keine Abweichung von den Newtonschen Axiomen.
Diese Trägheitskraft wurde 1775 von Pierre-Simon Laplace aus den newtonschen Gesetzen der Mechanik hergeleitet. Benannt wurde sie aber nach Gaspard Gustave de Coriolis, der sie 1835 ausführlich in einer Veröffentlichung behandelt hat.
Zu den Newtonschen Axiomen und Beschleunigung haben wir im Übrigen schon zwei Videos für dich vorbereitet. Schau sie dir zur Ergänzung hierzu am besten nochmal an.
Corioliskraft auf der Erde
Bei allen Bewegungen in rotierenden Systemen wirkt die Corioliskraft auf Körper, welche sich senkrecht zur Drehachse bewegen. Sie macht sich vor allem bei großräumigen Bewegungen, wie Luftströmungen zwischen Hoch- und Tiefdruckgebieten bemerkbar. Die Luftströme werden von der Corioliskraft auf Kreisbahnen gezwungen, was zu den bekannten Satellitenaufnahmen von Wolkenwirbeln führt. Dabei bewegen sich die Luftströmungen auf der Südhalbkugel entgegen dem Uhrzeigersinn und auf der Nordhalbkugel im Uhrzeigersinn. Da die Erde eine kugelförmige Gestalt hat und in 24 Stunden einmal um ihre eigene Achse rotiert, ist die Bahngeschwindigkeit auf der Erde von dem Breitengrad abhängig. Sie ist dabei am Äquator am größten und nimmt zu den Polen (Nordpol, Südpol) hin ab. Im folgenden zeigen wir zuerst, weshalb es auf der Nordhalbkugel zu einer Ablenkung im Uhrzeigersinn kommt und anschließend betrachten wir die Ablenkung entgegen dem Uhrzeigersinn auf der Südhalbkugel.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Ablenkung auf der Nordhalbkugel
Betrachten wir nun, in welche Richtung man auf der Nordhalbkugel abgelenkt wird, wenn man sich vom Äquator nach Norden bewegt oder umgekehrt. Angenommen wir befinden uns auf dem Äquator und fliegen direkt in Richtung Norden, dann behalten wir die Bahngeschwindikeit vom Äquator bei. Da jedoch die Bahngeschwindigkeit der Erde unter uns in Richtung Nordpol immer kleiner wird und wir aber die Bahngeschwindigkeit des Äquators beibehalten, eilen wir sozusagen der Erdoberfläche voraus. Dies resultiert, von oben betrachtet, zu einer Ablenkung im Uhrzeigersinn. Die gleichen Überlegungen kann man nun anstellen, wenn man von einem Ort auf der Nordhalbkugel in Richtung Äquator fliegt. Dann hat man eine kleinere Bahngeschwindigkeit als am Äquator. Je weiter wir in Richtung Äquator fliegen, desto größer wird die Bahngeschwindigkeit der Erde unter uns. Von oben betrachtet werden wir im Uhrzeigersinn abgelenkt.
Ablenkung auf der Südhalbkugel
Nun möchten wir noch kurz betrachten, wie man auf einer Strecke vom Äquator zum Südpol oder umgekehrt abgelenkt wird. Starten wir vom Äquator aus in Richtung Südpol, so besitzen wir wieder die Bahngeschwindigkeit des Äquators. Je weiter wir nach Süden kommen, desto stärker werden wir mit Blick in Richtung Süden nach links abgelenkt, also von oben entgegen dem Uhrzeigersinn. Genau dieselben Überlegungen kann man nun anstellen, wenn man von einem Ort auf der Südhalbkugel in Richtung Äquator fliegt. Auch hier ist die Ablenkung von oben betrachtet entgegen dem Uhrzeigersinn, da wir eine langsamere Bahngeschwindigkeit haben, als die Erde unter uns.
Passatwinde
Auch die Richtung der Passatwinde wird im Wesentlichen von der Corioliskraft beeinflusst. Aufgrund der starken Sonneneinstrahlung, erwärmen sich die Luftmassen am Äquator und steigen in die Höhe. Es entsteht dadurch am Äquator ein Tief. In einer bestimmten Höhe, fließen die Lufmassen in Richtung Norden und Süden ab und werden kälter weshalb sie wieder absinken. Dadurch entsteht dann ein Hoch. Da Luft immer von einem Hoch zu einem Tief strömt, entstehen Winde in Richtung Äquator, an welchem die Luftmassen wieder erwärmt werden und aufsteigen. Damit ist der Kreislauf geschlossen. Es bleibt nur noch die Frage der Ablenkung der Winde zu klären. Man unterscheidet den Nordost-Passat und den Südost-Passat. Betrachten wir zunächst den Nordost-Passat. Die Richtung eines Windes bezeichnet man immer aus welcher Richtung er kommt. Der Nordost-Passt kommt also aus Nordost. Der Grund hierfür liegt darin, dass die Luftmassen von der Nordhalbkugel in Richtung Äquator fließen, also vom Hoch zum Tief. Wie oben erklärt werden die Winde dann im Uhrzeigersinn abgelenkt. Das führt dazu, dass die Winde dann in der Nähe des Äquators aus Nordost kommen. Analog kann man sich das für die Südhalbkugel klar machen.
Wasserströmungen
Die gleichen Betrachtungen, welche wir für die Nord- und Südhalbkugel angestellt haben, gelten auch für Wasserströmungen beziehungsweise Meeresströmungen . Auch hier bewirkt die Corioliskraft eine Ablenkung auf der Nordhalbkugel im Uhrzeigersinn und auf der Südhalbkugel entgegen dem Uhrzeigersinn. Damit lässt sich auch erklären, weshalb zum Beipsiel der Golfstrom auf dem Weg nach Norden, gen Osten abknickt und große Teile Nordeuropas erwärmt.
Wirbelwinde
Die Corioliskraft ist auch an der Entstehung von Wirbelstürmen beteiligt. Diese Stürme können Durchmesser von einigen hundert Kilometern durchmessen. Dies geschieht, indem die feuchtheißen Luftströme durch die Kraft zu rotieren beginnen, bis die zerstörerischen Wirbel entstehen.
Foucaultsches Pendel
Mit dem Foucaultschen Pendel kann man die Erdrotation nachweisen. Dieses große, sphärische Pendel ermöglicht diesen Nachweis ohne die Notwendigkeit für vergleichende Himmelsbeobachtungen.
Corioliskraft Formel
Zur Berechnung der Coriolisbeschleunigung benutzt du die Formel
 .
.
Hierbei steht  für die Coriolisbeschleunigung,
für die Coriolisbeschleunigung,  für die vektorielle Winkelgeschwindigkeit
und
für die vektorielle Winkelgeschwindigkeit
und  für die Geschwindigkeit des Körpers.
für die Geschwindigkeit des Körpers.
Da du jetzt die Beschleunigung hast, kannst du analog zum newtonschen Gesetz, damit die zugehörige Corioliskraft definieren.

Herleitung mit Newtonscher Mechanik
Zur Herleitung der Corioliskraft anhand der newtonschen Mechanik betrachtest du ein Bezugssystem  . Dieses befindet sich in einem Inertialsystem
. Dieses befindet sich in einem Inertialsystem  . Dein Bezugssystem
. Dein Bezugssystem  rotiert mit der Winkelgeschwindigkeit
rotiert mit der Winkelgeschwindigkeit  und hat einen in
und hat einen in  fest verankerten Ursprung. Dadurch treten keine weiteren Relativbewegungen neben der Rotation auf. Schau dir am besten noch unser für dich erstelltes Video zur Winkelgeschwindigkeit
an, damit du für die kommende Herleitung hinreichend vorbereitet bist.
fest verankerten Ursprung. Dadurch treten keine weiteren Relativbewegungen neben der Rotation auf. Schau dir am besten noch unser für dich erstelltes Video zur Winkelgeschwindigkeit
an, damit du für die kommende Herleitung hinreichend vorbereitet bist.
Vom newtonschen Gesetz weißt du, dass das Produkt aus der Masse  und der Beschleunigung
und der Beschleunigung  im Inertialsystem gleich der Kraft
im Inertialsystem gleich der Kraft  ist
ist
 .
.
Da du eine analoge Gleichung im Bezugssystem aufstellen willst, müssen deine Bewegungsgrößen im Inertialsystem durch Größen wie sie im Bezugssystem beobachtet werden können, ausgedrückt werden. Für dein Bezugssystem  sind das der Ortsvektor
sind das der Ortsvektor  , die Geschwindigkeit
, die Geschwindigkeit  und die Beschleunigung
und die Beschleunigung  . Beachte dabei, dass sich die im Inertialsystem zu beobachtende Geschwindigkeit aus der Geschwindigkeit
. Beachte dabei, dass sich die im Inertialsystem zu beobachtende Geschwindigkeit aus der Geschwindigkeit  und der umlaufenden Bahngeschwindigkeit
und der umlaufenden Bahngeschwindigkeit  zusammensetzt. Daher gilt
zusammensetzt. Daher gilt
 .
.
Leitest du dies nach der Zeit ab erhältst du die Beschleunigung
 .
.
Formst du diesen Ausdruck nach 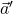 um, so ergibt sich
um, so ergibt sich
 .
.
Multiplizierst du jetzt die Masse und berücksichtigst das zweite newtonsche Gesetz  so ergibt sich dieBewegungsgleichung zu
so ergibt sich dieBewegungsgleichung zu
 .
.
Mit dieser Gleichung hast du die äußere Kraft und alle Trägheitskräfte im rotierenden Bezugssystem zusammengefasst. Der letzte Term ist die Corioliskraft
 .
.
Herleitung mit Lagrange Formalismus
Bei diesem Ansatz brauchst du den Lagrange Formalismus. Das ist eine umfassendere Thematik zu der du dir am besten das für dich vorbereitete Video anschaust.
Die Lagrangefunktion ist die Differenz aus kinetischer Energie und potentieller Energie. Vernachlässigst du das Potential so erhältst du
 .
.
Nach den Euler-Lagrange-Gleichungen ist
 .
.
Da die Euler-Lagrange-Gleichungen invariant unter Koordinatentransformationen sind, folgt im bewegten Bezugssystem

und
 .
.
Setzt du das in die Euler-Lagrange-Gleichung ein und formst nach  um, erhältst du
um, erhältst du
 .
.
In diesem Ausdruck erkennst du erneut, dass der letzte Term die Corioliskraft zeigt.
Corioliskraft berechnen
Zur besseren Veranschaulichung erhältst du hier ein kleines Rechenbeispiel zur Corioliskraft.
Ein Panzer der Masse 50.000 t fährt mit 80 km/h in Mainz, bei  nördlicher Breite, von Norden nach Süden. Wie groß ist der Betrag der Corioliskraft?
nördlicher Breite, von Norden nach Süden. Wie groß ist der Betrag der Corioliskraft?
Lösung:
Die Corioliskraft wird ausgedrückt durch:

Daraus folgt für den Betrag:

Hier setzt du nun einfach die gegebenen Werte ein.
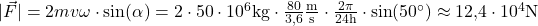
Damit ergibt sich für die Corioliskraft ein Wert von ungefähr  .
.
Coriolisbeschleunigung
Stell dir vor, dass du auf einer rotierenden Scheibe stehst. So lange du einfach mit rotierst wirkt nur die nach außen gerichtete Zentrifugalkraft auf dich. Versuchst du dich von der Drehachse zu entfernen oder läufst um die Drehachse herum so musst du Kraft aufwenden. Das Prinzip dahinter wird dir in Folge erklärt.
Coriolisbeschleunigung bei radialer Bewegung
Erhält dein, sich mit der Scheibe rotierender, Körper eine Radialgeschwindigkeit, legt dieser eine Strecke  in der Zeit
in der Zeit  zurück.
zurück.
Bei einer gradlinigen Bewegung, würde der Körper den Endpunkt von Linie 1 erreichen. In deinem Laborsystem bewegt sich der Körper entlang der Vektorsumme aus dem tangentialen und radialen Pfeil zum Endpunkt 2. Jedoch dreht sich die Scheibe in dieser Zeit um den Winkel  weiter, womit sich der erwartete Endpunkt 1 weiterbewegt zu 3. Wegen
weiter, womit sich der erwartete Endpunkt 1 weiterbewegt zu 3. Wegen
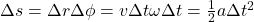
wächst  quadratisch mit der Zeit, was einer gleichmäßigen Coriolisbeschleunigung entspricht:
quadratisch mit der Zeit, was einer gleichmäßigen Coriolisbeschleunigung entspricht:
 .
.
Coriloisbeschleunigung bei Kreisbewegung
Im Zeitraum  bewirkt eine Beschleunigung eine radiale Bewegung um die Strecke
bewirkt eine Beschleunigung eine radiale Bewegung um die Strecke  . Durch Anwendung des Satzes des Pythagoras und einer Gleichsetzung des roten Kreisbogens mit der kleinen Kathete, kommt man zu diesem Schluss. Diese beiden Seiten kann man gleichsetzen indem man den Kreisbogen durch infinitesimale Intervalle annähert. Daraus ergibt sich
. Durch Anwendung des Satzes des Pythagoras und einer Gleichsetzung des roten Kreisbogens mit der kleinen Kathete, kommt man zu diesem Schluss. Diese beiden Seiten kann man gleichsetzen indem man den Kreisbogen durch infinitesimale Intervalle annähert. Daraus ergibt sich
 .
.
Anhand der quadratischen Abhängigkeit siehst du, dass eine konstante Beschleunigung vorliegt
 .
.
Abhängig von der Bedeutung von  und
und  , kannst du dieses Ergebnis verschieden auswerten.
, kannst du dieses Ergebnis verschieden auswerten.
Gilt  erhältst du die Zentripetalkraft, die bei jeder Kreisbewegung entsteht.
erhältst du die Zentripetalkraft, die bei jeder Kreisbewegung entsteht.
Hat der Körper jedoch zusätzlich eine Relativgeschwindigkeit  zur Rotation, so ergibt sich folgendes
zur Rotation, so ergibt sich folgendes
 .
.
Die Summe im Laborsystem ist die Summe aus Umlaufgeschwindigkeit und Relativgeschwindigkeit  . Ist die Drehgeschwindigkeit der Scheibe durch
. Ist die Drehgeschwindigkeit der Scheibe durch  gegeben, erhältst du die Umlaufgeschwindigkeit
gegeben, erhältst du die Umlaufgeschwindigkeit  . Das eingesetzt ergibt dann die Zentripetalbeschleunigung
. Das eingesetzt ergibt dann die Zentripetalbeschleunigung
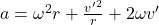 .
.
Diese Gleichung zeigt, dass sich die Zentripetalbeschleunigung aus den drei Summanden, nämlich der Zentrifugalbeschleunigung, der Beschleunigung in Rotationsrichtung, sowie der Coriolisbeschleunigung, zusammensetzt. Die Aufteilung dieser radialen Komponenten ist abhängig vom gewählten Bezugssystem und damit willkürlich.




