Arbeit und Energie
In diesem Beitrag zeigen wir dir, wie du die Arbeit und Energie berechnen kannst. Dabei gehen wir zunächst auf die Arbeit ein und beschäftigen uns dann mit den verschiedenen Energieformen, wie die kinetische und potentielle Energie . Auch übertragen wir das ganze auf Massenpunktsysteme.
Falls du keinen physikalischen Text lesen möchtest, erklären wir dir das alles in Kürze in unserem Video .
Inhaltsübersicht
Arbeit und Energie berechnen
Arbeit und Energie sind Weg– bzw. Ortsabhängige Größen, die durch Kräfte und Momente hervorgerufen werden. Die Arbeit entspricht dabei der Änderung der Energie eines Systems. Das Formelzeichen für die Arbeit ist 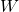 und die Einheit ist Joule
und die Einheit ist Joule 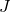 . Bei der Energie ist das Zeichen meistens ein
. Bei der Energie ist das Zeichen meistens ein 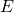 und die Einheit ebenfalls Joule
und die Einheit ebenfalls Joule 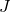 .
.
Der Begriff der Arbeit
Der Begriff der Arbeit ist definiert über die Kraft 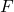 und den Weg
und den Weg  :
:
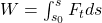
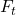 steht dabei für die ortsabhängige Tangentialkraft, mit der wir die kinetische Energie herleiten können. Das heißt wir betrachten nur die Kraftkomponente, die tangential zur Bahnkurve ist und können direkt ein skalares Integral bilden. Die Kraft
steht dabei für die ortsabhängige Tangentialkraft, mit der wir die kinetische Energie herleiten können. Das heißt wir betrachten nur die Kraftkomponente, die tangential zur Bahnkurve ist und können direkt ein skalares Integral bilden. Die Kraft 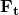 kann auch wie folgt mit der Beschleunigung
kann auch wie folgt mit der Beschleunigung  , beziehungsweise der Geschwindigkeit
, beziehungsweise der Geschwindigkeit  und der Zeit
und der Zeit 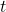 umgeschrieben werden.
umgeschrieben werden.
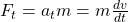
Da wir eine Lösung für das Integral 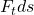 suchen, müssen wir den Term für
suchen, müssen wir den Term für 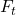 mit
mit 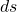 erweitern. Um nun den entstandenen Term zu vereinfachen, können wir die Kettenregel rückwärts anwenden und erhalten:
erweitern. Um nun den entstandenen Term zu vereinfachen, können wir die Kettenregel rückwärts anwenden und erhalten:
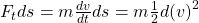
Jetzt setzen wir das Ganze in die Arbeit ein:
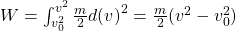
Die Formel erinnert dich wahrscheinlich an die kinetische Energie. Die Arbeit beschreibt in diesem Fall also die Differenz der kinetischen Energie zwischen zwei Zuständen mit der Anfangsgeschwindigkeit 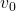 und der Endgeschwindigkeit
und der Endgeschwindigkeit  .
.
Falls du mehr zu der Arbeit wissen möchtest, kannst du das Video zu unserem Artikel zur mechanischen Arbeit und den konservativen Kräften anschauen.
Energieformen
Die kinetische Energie wird auch Bewegungsenergie genannt. Neben dieser gibt es noch die potentielle Energie bzw. die Höhenenergie. Sie entsteht, indem ein Körper entgegen der Schwerkraft angehoben wird und so im Körper als Höhenenergie gespeichert wird. Fällt der Körper wieder zu Boden wird sie als potentielle Energie
wiedergewonnen. Bei der potentiellen Energie setzt man sich ein Nullniveau, da sie sich schwer als absoluten Wert festlegen lässt. Denn wenn ein Gegenstand auf einem Tisch steht, so besitzt er gegenüber dem Boden meist eine andere Höhenenergie als gegenüber dem Meeresspiegel. Die Energie kann dabei auch negativ sein, falls die Höhe „negativ“ ist.
Die kinetische und die potentielle Energie beschreiben zusammen die Energiezustände eines Massenpunkts. Es gilt dabei die:
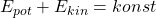
Betrachten wir nun die Bewegung eines Massenpunkts: Zu Beginn hat der Massenpunkt die potentielle Energie 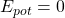 und die kinetische Energie
und die kinetische Energie 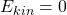 . Betrachten wir den Punkt zu einem späteren Zeitpunkt, also wenn sich der Punkt auf der Bahnkurve weiterbewegt hat, sehen wir, dass sich sowohl der Ort des Massenpunkts als auch die potentielle Energie verändert hat. Gemäß der Energieerhaltung muss sich also auch die kinetische Energie ändern und wir erhalten:
. Betrachten wir den Punkt zu einem späteren Zeitpunkt, also wenn sich der Punkt auf der Bahnkurve weiterbewegt hat, sehen wir, dass sich sowohl der Ort des Massenpunkts als auch die potentielle Energie verändert hat. Gemäß der Energieerhaltung muss sich also auch die kinetische Energie ändern und wir erhalten:
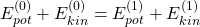
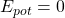 und
und 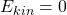 beschreiben hier die potentielle bzw. kinetische Energie zum anfänglich betrachteten Zeitpunkt.
beschreiben hier die potentielle bzw. kinetische Energie zum anfänglich betrachteten Zeitpunkt. 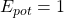 und
und 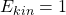 hingegen beschreiben die potentielle bzw. kinetische Energie zu einem späteren Zeitpunkt.
hingegen beschreiben die potentielle bzw. kinetische Energie zu einem späteren Zeitpunkt.
Energiesatz bei Massenpunktsystemen
Da aber in der Dynamik nicht nur Massenpunkte, sondern auch Massenpunktsysteme relevant sind, müssen wir auch deren Energiesatz anschauen. Wir betrachten also 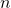 -Massenpunkte, die miteinander verbunden sind. Es gilt grundsätzlich wieder die Energieerhaltung. Nur mit der Ausnahme, dass zusätzlich nur die innere potentielle Energie miteinbezogen werden muss, die aus den Verbindungen zwischen den Massenpunkten entsteht. In der Mechanik stellt man sich diese Verbindungen als Federn vor. Zu Beginn betrachten wir die die kinetische Energie. Bei dieser gilt allgemein:
-Massenpunkte, die miteinander verbunden sind. Es gilt grundsätzlich wieder die Energieerhaltung. Nur mit der Ausnahme, dass zusätzlich nur die innere potentielle Energie miteinbezogen werden muss, die aus den Verbindungen zwischen den Massenpunkten entsteht. In der Mechanik stellt man sich diese Verbindungen als Federn vor. Zu Beginn betrachten wir die die kinetische Energie. Bei dieser gilt allgemein:
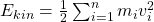
Da der Schwerpunkt des Massenpunktsystems nicht in den einzelnen Massenpunkten liegt, müssen wir zusätzlich die Differenzgeschwindigkeit zur Schwerpunktgeschwindigkeit 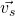 betrachten. Dies setzen wir in die Formel für die kinetische Energie ein und multiplizieren den Term aus. Das sieht dann so aus:
betrachten. Dies setzen wir in die Formel für die kinetische Energie ein und multiplizieren den Term aus. Das sieht dann so aus:
Wir nutzen beim ersten Term aus, dass die Summe über alle Massenpunkte gleich der Gesamtmasse ist und 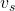 konstant bleibt. Dadurch ergibt sich:
konstant bleibt. Dadurch ergibt sich:
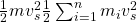
Als nächstes betrachten wir die mittlere Summe und werden feststellen, dass diese gleich 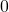 ist. Dazu setzen wir die Gleichung für die Differenzgeschwindigkeit wieder ein und nutzen, dass die Schwerpunktgeschwindigkeit unabhängig vom Massenpunkt ist. Danach können wir dann umformen und erhalten:
ist. Dazu setzen wir die Gleichung für die Differenzgeschwindigkeit wieder ein und nutzen, dass die Schwerpunktgeschwindigkeit unabhängig vom Massenpunkt ist. Danach können wir dann umformen und erhalten:
Nun können wir die Definition des Schwerpunkts verwenden:
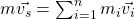
Um die zweite Summe zu lösen, verwenden wir die Tatsache, wie vorher, dass die Summe über alle Massen gleich der Gesamtmasse ist. Dadurch ergibt sich:
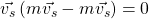
Die kinetische Energie eines Körpers besteht also aus der kinetischen Energie, wenn die gesamte Masse im Schwerpunkt ist und der Relativbewegung der Massenpunkte zum Schwerpunkt. Die Relativbewegung ist in der Regel eine Drehung um den Schwerpunkt.
Potentielle Energie
Nachdem wir die kinetische Energie betrachtet haben, schauen wir uns als nächstes die potentielle Energie an. Wie du vielleicht noch weißt, ist die potentielle Energie das Resultat der Gewichtskraft. Die Gewichtskraft selbst greift immer im Schwerpunkt an, sodass die potentielle Energie für Massenpunktsysteme gleich der potentiellen Energie für einen einzelnen Massenpunkt ist:
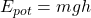
Zum Schluss betrachten wir die innere potentielle Energie. Wie du schon weißt, stellt man sich in der Mechanik die Verbindungen zwischen den Massenpunkten als Federn vor. Wir betrachten jetzt den Zustand einer Feder vor, die du parallel zum Boden eindrückst. Du hast Energie aufgewendet, um sie zusammen zu drücken, allerdings ist keine Höhendifferenz vorhanden. Dementsprechend benötigst du die innere potentielle Energie, um den Energieerhaltungssatz zu entsprechen.
Die innere potentielle Energie einer Feder ergibt sich also aus der Arbeit der Federkraft über den Weg:
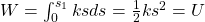
Die Federkraft greift, wie die Gewichtskraft immer im Schwerpunkt an, sodass auch hier keine Relativbewegung betrachtet werden muss.
Schauen wir uns nun alle Energien an, können wir die verrichtete Arbeit darstellen durch:
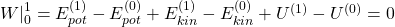
Die Arbeit bildet sich also aus den Differenzen der kinetischen, der potentiellen und der inneren potentiellen Energie. Das heißt wir betrachten die Energiedifferenz zwischen zwei Punkten. Diese ist gemäß der Energieerhaltung gleich Null.
Bislang haben wir nur die Arbeit bzw. Energie betrachtet, die durch Kräfte hervorgerufen wird, damit die Herleitung nicht zu komplex wird. Bei Momenten ist es etwas komplizierter. Der Unterschied in der Berechnung ist, dass nicht über einen Weg integriert wird, sondern über den Drehwinkel:
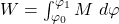
Dabei werden Momente, die von außen angreifen, der kinetischen Energie zugeordnet. Momente, die durch eine Drehfeder erzeugt werden, gehören zur inneren potentiellen Energie.
Mit der Arbeit bzw. der Energie haben wir also die Möglichkeit ein System vollständig zu beschreiben. So kann man vergleichsweise komplexe Systeme einfach darstellen.

