Arbeit und Energie Übung
Du willst wissen wie du Arbeit und Energie am schnellsten berechnest? Das zeigen wir dir in diesem Beitrag an dem Beispiel eines Festlagers berechnet.
Inhaltsübersicht
Arbeit und Energie berechnen
Zu Beginn gehen wir noch einmal kurz die Grundlagen durch. Wir unterscheiden zwischen drei verschiedenen Arten von Energien: der kinetischen Energie
, der potentiellen und der inneren potentiellen Energie
. Letztere wird dabei nur beim Einsatz von Federn betrachtet. Die kinetische Energie 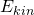 ist definiert durch:
ist definiert durch:
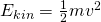
Dabei ist 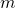 die Masse des Körpers und
die Masse des Körpers und  seine Geschwindigkeit. Die potentielle Energie
seine Geschwindigkeit. Die potentielle Energie 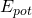 ergibt sich mit dem Ortsfaktor
ergibt sich mit dem Ortsfaktor 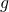 und der Höhe
und der Höhe 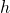 durch:
durch:
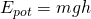
Die innere potentielle Energie 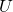 lässt sich für eine Feder mathematisch wie folgt formulieren:
lässt sich für eine Feder mathematisch wie folgt formulieren:
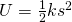
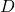 ist die Federkonstante und
ist die Federkonstante und  die Auslenkung aus der Ruhelage. Für eine Drehfeder gilt:
die Auslenkung aus der Ruhelage. Für eine Drehfeder gilt:
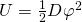
Mit dem Direktionsmoment 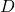 und dem Auslenkungswinkel
und dem Auslenkungswinkel 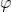 .
.
Innere potentielle Energie
Bei der inneren potentiellen Energie müssen wir zwischen einer normalen Feder, die du aus dem Alltag kennst, und einer sogenannten Drehfeder unterscheiden, die nur ein Moment verursacht. Dabei bilden 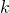 bzw.
bzw. 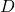 die Federkonstante der Feder bzw. Drehfeder. Bei der potentiellen Energie ist noch zu beachten, dass wir uns die sogenannte Nullniveau-Linie selbst definieren müssen und
die Federkonstante der Feder bzw. Drehfeder. Bei der potentiellen Energie ist noch zu beachten, dass wir uns die sogenannte Nullniveau-Linie selbst definieren müssen und 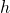 somit nur der Abstand zu dieser Linie ist. Dieser kann auch negativ sein, falls wir uns unterhalb der Linie befinden. Die Nullniveau-Linie ist die Referenzlinie, bei der die potentielle Energie gleich Null ist. Dabei kannst du dir selbst überlegen, wo du die Nullniveau-Linie platzierst, um die Rechnung zu vereinfachen. Um nun Bewegungsgleichungen aufzustellen, muss die Energieerhaltung gelten. Das heißt, dass die Summe aus den drei Energien konstant sein muss!
somit nur der Abstand zu dieser Linie ist. Dieser kann auch negativ sein, falls wir uns unterhalb der Linie befinden. Die Nullniveau-Linie ist die Referenzlinie, bei der die potentielle Energie gleich Null ist. Dabei kannst du dir selbst überlegen, wo du die Nullniveau-Linie platzierst, um die Rechnung zu vereinfachen. Um nun Bewegungsgleichungen aufzustellen, muss die Energieerhaltung gelten. Das heißt, dass die Summe aus den drei Energien konstant sein muss!
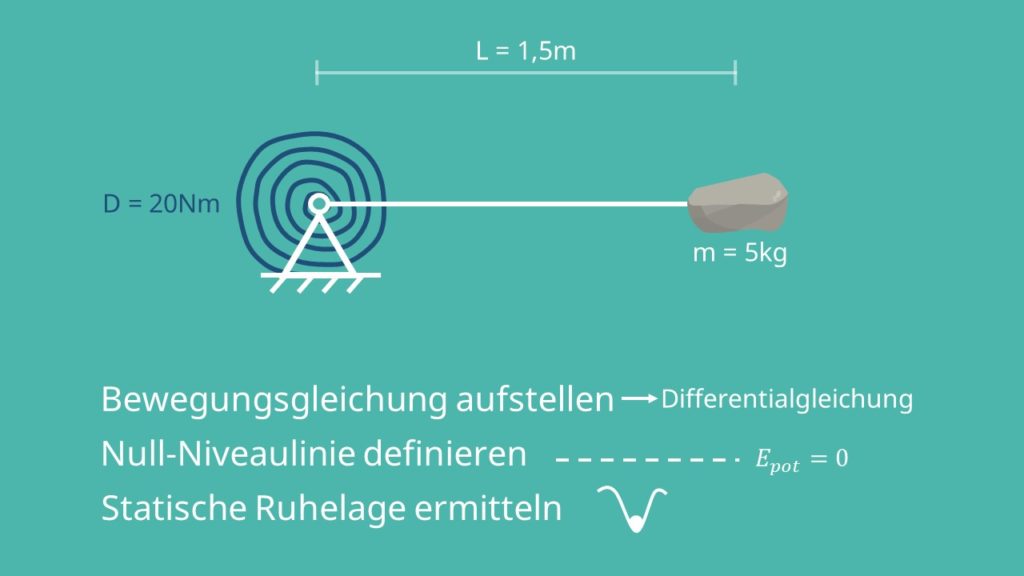
Beispiel Festlager
Nun zum Beispiel: Eine Masse mit dem Gewicht 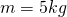 ist durch einen Stab der Länge
ist durch einen Stab der Länge 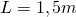 an einem Festlager angebracht und wird durch eine Drehfeder mit der Federkonstante
an einem Festlager angebracht und wird durch eine Drehfeder mit der Federkonstante 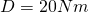 an der Drehbewegung gehindert. Die Feder ist dabei am Festlager fixiert.
an der Drehbewegung gehindert. Die Feder ist dabei am Festlager fixiert.
Nun möchten wir die Bewegungsgleichung aufstellen, damit wir das System zu jedem Zeitpunkt vollständig beschreiben können. Hier bedeutet es, dass du eine Differentialgleichung aufstellst. Die Lösung müssen wir dabei allerdings nicht betrachten, da die Differentialgleichung das System bereits vollständig beschreibt.
Zu Beginn musst du die Null-Niveaulinie definieren, damit wir einen Referenzwert zur Bestimmung der potentiellen Energie haben. Wir ermitteln zusätzlich die statische Ruhelage, also den Ort, an dem wir ein Kräfte- und Momentengleichgewicht haben. Denn das System bewegt sich immer um die Ruhelage. Dazu kannst du dir ein Pendel vorstellen: Es schwingt immer um den Punkt herum, an dem der Faden senkrecht nach unten zeigt, solange bis es sich nicht mehr bewegt.
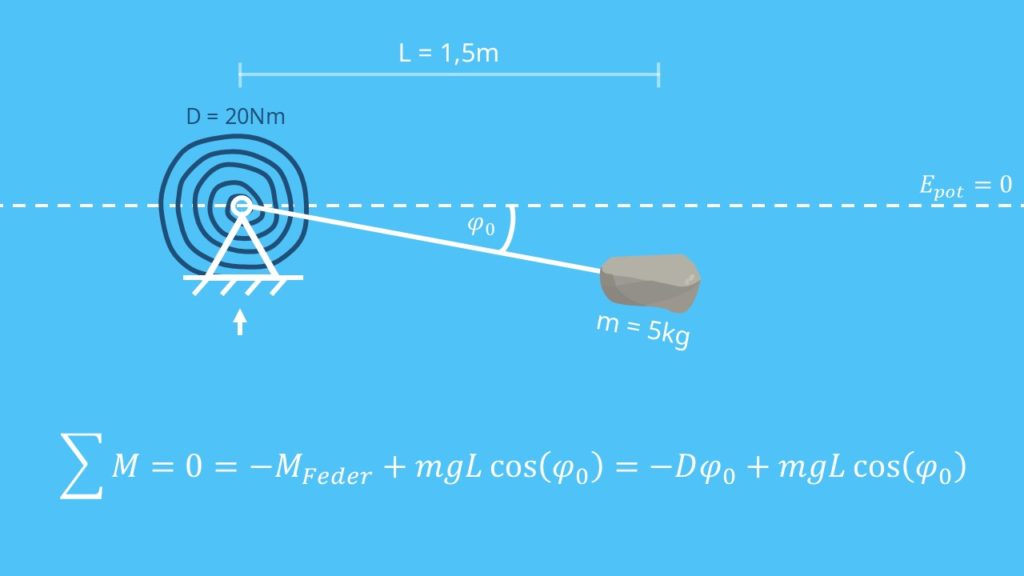
Die Nullniveau-Linie ziehen wir parallel zum Boden genau durch das Gelenk, an dem die Stange festgemacht ist. Das heißt: wenn der Stab waagerecht ist, liegt dieser genau auf der Nullniveau-Linie. Für die statische Ruhelage bilden wir ein Momentengleichgewicht am Festlager. Dabei müssen wir beachten, dass die Lage an einem Ort um den Winkel 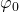 nach unten verschoben wird. Daraus ergibt sich:
nach unten verschoben wird. Daraus ergibt sich:
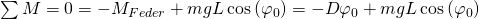
Das formen wir um und erhalten für die statische Ruhelage:
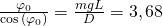
Das zu lösen ist jetzt rein algebraisch nicht mehr möglich. Deshalb treffen wir eine Vereinfachung in Form der Kleinwinkelnäherung und behaupten, dass 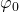 sehr klein ist. Die Kleinwinkelnäherung besagt, dass bei kleinen Winkeln der Sinus gleich
sehr klein ist. Die Kleinwinkelnäherung besagt, dass bei kleinen Winkeln der Sinus gleich 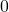 , beziehungsweise der Cosinus gleich
, beziehungsweise der Cosinus gleich 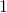 ist. Damit können wir Cosinus
ist. Damit können wir Cosinus 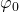 gleich
gleich 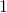 setzen und erhalten, dass
setzen und erhalten, dass 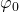 einen Radiant von 3,68 hat.
einen Radiant von 3,68 hat.
Ermittlung der Bewegungsgleichung
Als nächstes ermitteln wir die Bewegungsgleichung, um das System vollständig zu beschreiben. Dazu stellen wir für die jeweiligen Energien die Gleichungen auf. Wir beginnen mit der kinetischen Energie:
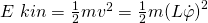
Da wir hier eine Kreisbewegung haben, kann die Geschwindigkeit der Masse durch die Winkelgeschwindigkeit, also der Änderung des Winkels 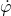 , dargestellt werden.
, dargestellt werden.
Als nächstes betrachten wir die potentielle Energie:
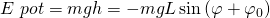
In unserem Beispiel geht die potentielle Energie positiv nach unten. Deshalb ist sie negativ. Zusätzlich haben wir noch die Anfangsauslenkung 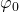 , die noch berechnet werden muss.
, die noch berechnet werden muss.
Zum Schluss betrachten wir die innere potentielle Energie:
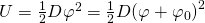
Auch hier muss die anfängliche Auslenkung miteinbezogen werden, da die Feder dadurch schon gespannt wird.
Jetzt stellen wir die Gleichung nach dem Energiesatz, bzw. der Energieerhaltung auf:
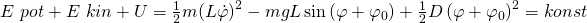
Da die Ableitung einer Konstanten gleich Null ist, müssen wir den Term nur noch nach der Zeit ableiten. Die einzelnen Terme ergeben sich zu:
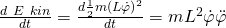
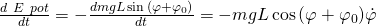
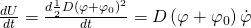
Dadurch erhalten wir für den gesamten Term:
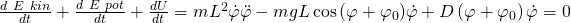
Am Ende stellen wir die Gleichung noch nach der höchsten Ableitung um und erhalten die Differenzialgleichung, die die Bewegung vollständig beschreibt:
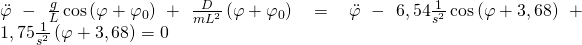
Wir nutzen also die Arbeit bzw. die Energie, um die Bewegungsgleichung in Form einer Differentialgleichung aufzustellen.
Du siehst: mit dem Energiesatz kannst du die Gleichung für die Bewegung eines Systems Schritt für Schritt ermitteln.