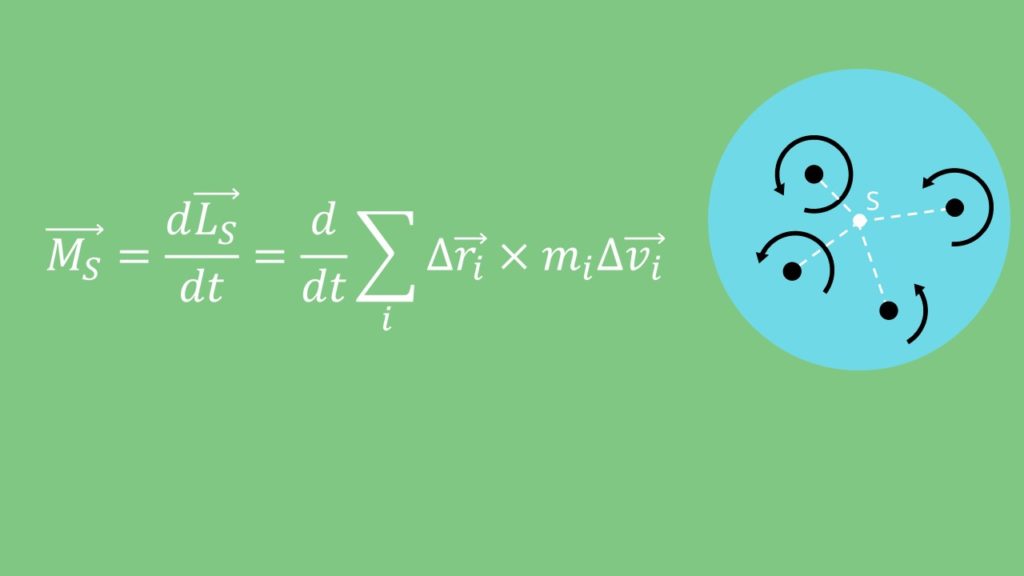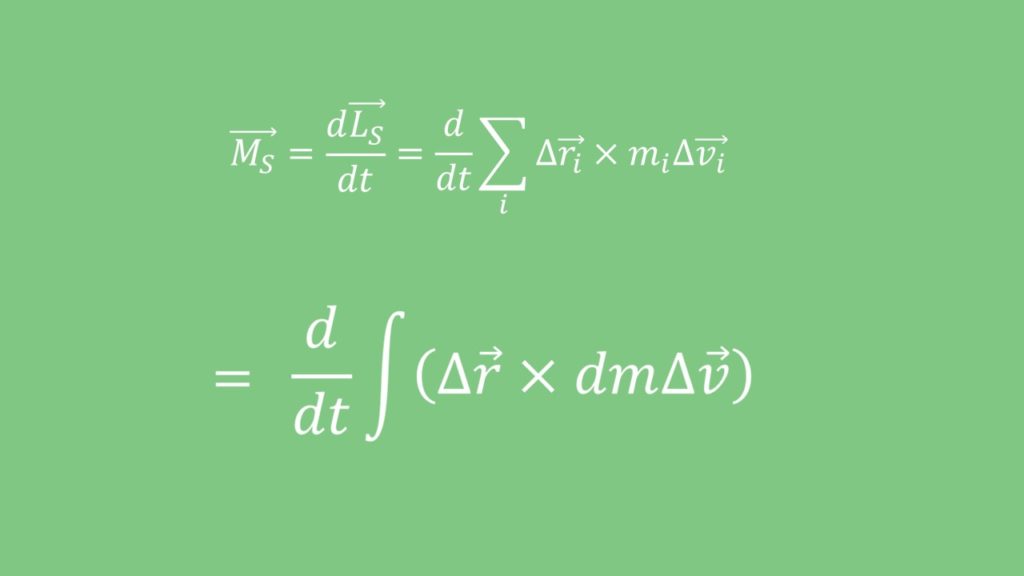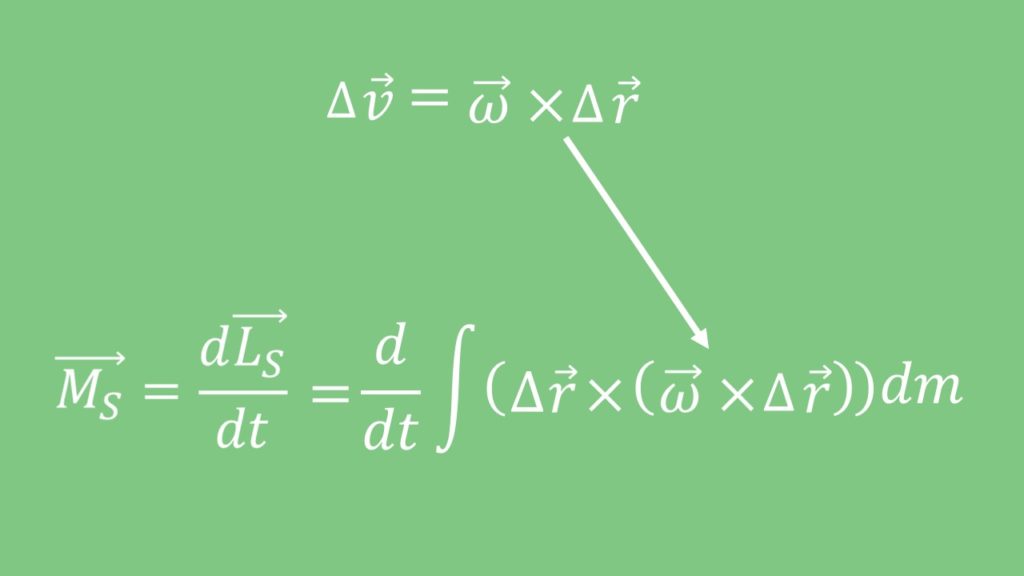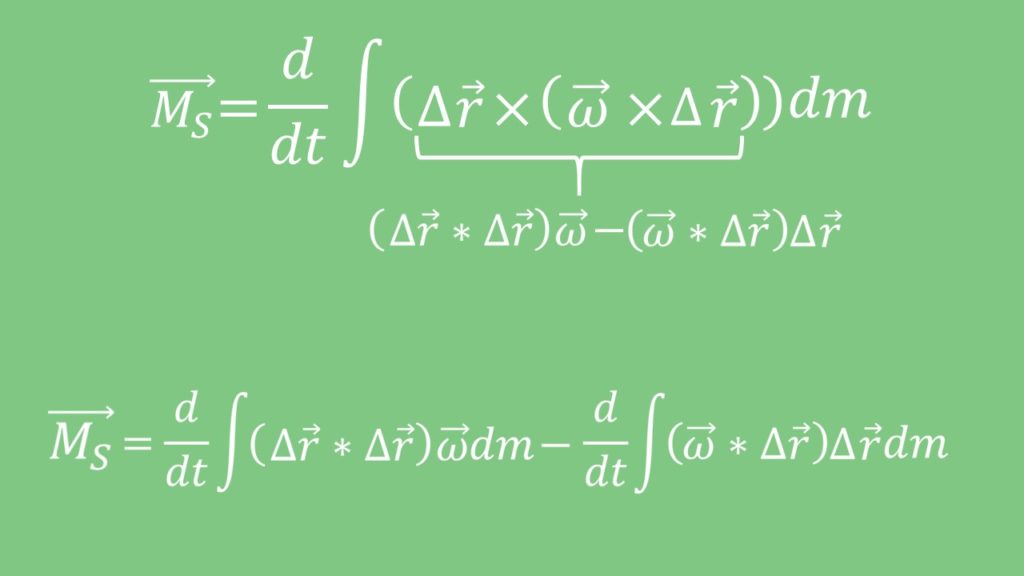Drallsatz
Der Drallsatz ist ein wichtiges Thema in der klassischen Mechanik und verbindet den Drehimpuls mit dem Drehmoment. Falls dir das alles zu viel physikalischer Text zum Lesen ist, schau dir doch unser Video zum Thema Drallsatz an! Dort erklären wir dir alles in kürzester Zeit.
Inhaltsübersicht
Drallsatz Formel
Der Drallsatz wird auch als Momentensatz oder Drehimpulssatz bezeichnet. Er gibt wieder, dass zu einer Veränderung des Drehimpulses eines physikalischen Objekts ein Drehmoment an diesem angebracht werden muss. Dieser Zusammenhang ist gleich dem bei der mechanischen Kraft. Durch eine zeitliche Veränderung des Impulses ergibt sich eine Kraft.
Falls du zu den Themengebiete Drehimpuls und Drehmoment mehr wissen willst, haben wir dir den jeweiligen Artikel verlinkt. Diese sind die Grundlagen zum Drall und sind für die Drallsatz Formel wichtig. Mathematisch lässt sich die Veränderung des Drehimpuls durch die zeitliche Ableitung schreiben. Damit ergibt sich folgende Drallsatz Formel:
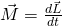
Das Drehmoment ist dabei 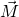 und der Drehimpuls
und der Drehimpuls 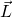 . Letzteres ist definiert durch:
. Letzteres ist definiert durch:
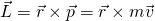
Dabei ist 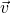 die Geschwindigkeit und
die Geschwindigkeit und 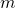 die Masse des betrachteten physikalischen Objekts. Dieser Zusammenhang ist in dem Video zum Impulserhaltungssatz
genauer erklärt.
die Masse des betrachteten physikalischen Objekts. Dieser Zusammenhang ist in dem Video zum Impulserhaltungssatz
genauer erklärt.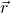 ist der Radius zu dem Körper vom Mittelpunkt der Kreisbewegung aus.
ist der Radius zu dem Körper vom Mittelpunkt der Kreisbewegung aus.
Drehimpulserhaltung
Genau wie bei dem Impuls gibt es auch für den Drehimpuls einen Erhaltungssatz. Dieser besagt, dass wenn in einem abgeschlossenen System kein Drehmoment wirkt, der Drehimpuls konstant ist. Damit handelt es sich um eine erneute Erhaltungsgröße. Mathematisch ausgedrückt:
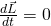
Das gilt aber nur, wenn kein Moment von außen auf das System wirkt. So gilt die Drehimpulserhaltung auch, wenn andere Kräfte anwesend sind, solange diese kein Drehmoment sind.
Drallsatz bei starren Körpern
Im Falle eines starren Körpers wird angenommen, dass dieser aus vielen, miteinander verbundenen Massenpunkten besteht. Weiterhin kann ausgenutzt werden, dass der Drall der einzelnen Massenpunkte zum Gesamtdrall 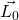 bezüglich des Ursprungs summiert werden kann:
bezüglich des Ursprungs summiert werden kann:
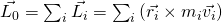
Der Laufindex 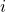 symbolisiert Massenpunkte. In diesen Summen wird über alle vorhandenen Massenpunkte aufsummiert. Mit der Hilfe des Drallsatzes können die Berechnungen umformuliert werden.
symbolisiert Massenpunkte. In diesen Summen wird über alle vorhandenen Massenpunkte aufsummiert. Mit der Hilfe des Drallsatzes können die Berechnungen umformuliert werden.
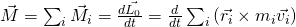
Momente
Auch die Momente werden bezüglich des Schwerpunktes betrachtet. So ergibt sich zunächst:
Dabei ist 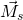 und
und 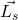 das Drehmoment und der Drehimpuls bezüglich des Schwerpunktes.
das Drehmoment und der Drehimpuls bezüglich des Schwerpunktes. 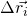 ist der Abstand des jeweiligen Massenpunktes vom Schwerpunkt und
ist der Abstand des jeweiligen Massenpunktes vom Schwerpunkt und 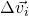 seine Geschwindigkeit in Relation zum Körperschwerpunkt. Letzteres wird durch eine Drehung verursacht. Um die Formel zu vereinfachen, wird über den ganzen Körper mit einer kontinuierlichen Masse von
seine Geschwindigkeit in Relation zum Körperschwerpunkt. Letzteres wird durch eine Drehung verursacht. Um die Formel zu vereinfachen, wird über den ganzen Körper mit einer kontinuierlichen Masse von 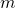 integriert, anstatt über die Massenpunkte aufzusummieren. Die Integrierung verlangt infinitesimal kleine Teilchen. Aus diesem Grund wird aus
integriert, anstatt über die Massenpunkte aufzusummieren. Die Integrierung verlangt infinitesimal kleine Teilchen. Aus diesem Grund wird aus 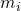 ,
, 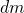 . Nun kann geschrieben werden:
. Nun kann geschrieben werden:
Die infinitesimal kleine Masse kann aus dem Kreuzprodukt herausgezogen werden.
Geschwindigkeit in Drehbewegungen
Aus der kinematischen Beziehung kann die Geschwindigkeit 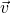 geschrieben werden als:
geschrieben werden als:
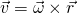
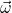 ist die Winkelgeschwindigkeit und
ist die Winkelgeschwindigkeit und 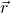 der Radius zum Mittelpunkt der Kreisbewegung. Daraus folgt:
der Radius zum Mittelpunkt der Kreisbewegung. Daraus folgt:
Mit der Hilfe der Graßmann-Identität kann das doppelte Kreuzprodukt vereinfacht werden.
Die Multiplikation von 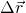 mit sich selbst im ersten Integral ergibt ein Betragsquadrat des Vektors. Des Weiteren lässt sich das
mit sich selbst im ersten Integral ergibt ein Betragsquadrat des Vektors. Des Weiteren lässt sich das 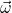 aus dem Integral ziehen, da es massenunabhängig ist.
aus dem Integral ziehen, da es massenunabhängig ist.
Auflösung
Das Skalarprodukt im zweiten Integral darf nicht herausgezogen werden. Um die Winkelgeschwindigkeit 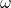 , die massenunabhängig ist, aus dem Integral hinausziehen zu können, muss jede Richtung des Vektors
, die massenunabhängig ist, aus dem Integral hinausziehen zu können, muss jede Richtung des Vektors 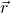 und
und 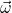 betrachtet werden.
betrachtet werden.
Wird dies mit dem ersten Integral verrechnet ergibt sich für die x-Richtung:
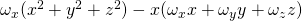
Bei der y-Richtung ergibt sich:
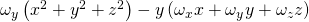
Und für die letzte Richtung, der z-Richtung:
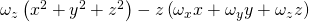
Durch Kürzungen erhält man für die x-Richtung:
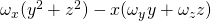
Bei der y-Achsenrichtung:
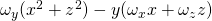
Und für die z-Richtung:
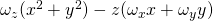
Das 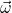 kann nun als kompletter Vektor ausgeklammert werden. Wichtig dabei ist, dass jetzt eine Matrix zurückbleibt. So wird folgendes Integral erhalten:
kann nun als kompletter Vektor ausgeklammert werden. Wichtig dabei ist, dass jetzt eine Matrix zurückbleibt. So wird folgendes Integral erhalten:
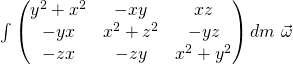
Das Integral über die Masse 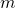 von der Matrix wird auch Massenträgheitsmoment
von der Matrix wird auch Massenträgheitsmoment 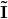 genannt. So ergibt sich für den Drallsatz bezüglich des Schwerpunktes:
genannt. So ergibt sich für den Drallsatz bezüglich des Schwerpunktes:
![Rendered by QuickLaTeX.com \vec{M_S}\ =\ \frac{d}{dt}\left[\int\left(\begin{matrix}y^2 + x^2&-xy&-xz\\-yx&x^2 + z^2&-yz\\-zx&-zy&x^2 + y^2\\\end{matrix}\right)\right]dm\vec{\omega} = \frac{d}{dt}\left[\vec{I_S}\dot{\vec{\omega}}}}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ca5be53958e103180f1772df5fbb89fc_l3.png)
Hauptachsensystem
Um die Matrix zu vereinfachen wird meistens ein Hauptachsensystem als Koordinatensystem verwendet. In diesem Fall werden alle Elemente, die nicht auf der Diagonalen sind, zu Null.
Ein Beispiel wird eine Punktmasse betrachtet, die sich auf einer Kreisbahn mit einem konstanten Radius  bewegt. Der Ursprung liegt genau in die Mitte des Kreises. Das Hauptachsensystem kommt zustande, wenn die x-Achse immer auf den Massenpunkt zeigt und sich somit mit dreht.
bewegt. Der Ursprung liegt genau in die Mitte des Kreises. Das Hauptachsensystem kommt zustande, wenn die x-Achse immer auf den Massenpunkt zeigt und sich somit mit dreht.
In diesem Fall sind die y- und die z-Koordinate immer null. Der x-Wert hingegen ist immer konstant und gleich dem Radius. Der Massenträgheitsmoment ergibt sich dann zu:
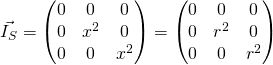
Daran kann erkannt werden, dass 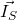 konstant sein muss, da der Radius konstant ist. So muss nur noch die Winkelbeschleunigung abgeleitet werden.
konstant sein muss, da der Radius konstant ist. So muss nur noch die Winkelbeschleunigung abgeleitet werden.
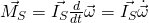
Drallsatz und Drehmoment
Mit der Hilfe des Drallsatzes kann die Formel für das Drehmoment aus dem Drehimpuls bestimmt werden. Der Satz ist:
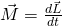
Die Ableitung des Impulses ergibt sich zu:
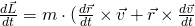
Da es sich bei der Masse um eine Konstante handelt, wird diese bei der Ableitung ausgeklammert. Nun ergibt sich:
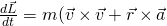
Das Kreuzprodukt eines Vektors mit sich selbst ergibt den Nullvektor. Damit fällt die Geschwindigkeit aus der Gleichung:
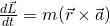
Mit der Beziehung, dass die Kraft 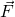 gleich Masse mal Beschleunigung ist, kann ersetzt werden.
gleich Masse mal Beschleunigung ist, kann ersetzt werden.
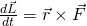
Das ist die Definition des Drehmoments 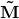 . An dieser Gleichung lässt sich feststellen, dass die zeitliche Änderung des Drehimpulses das Drehmoment ergibt.
. An dieser Gleichung lässt sich feststellen, dass die zeitliche Änderung des Drehimpulses das Drehmoment ergibt.