Drehmoment berechnen
Wie du das Drehmoment berechnest und welche Formeln du dazu brauchst, erfährst du in diesem Beitrag und im Video dazu!
Schau dir unsere Videos zu Übungsaufgaben und Klausuraufgaben an, um dich perfekt auf die Anwendung vorzubereiten!
Inhaltsübersicht
Drehmoment berechnen einfach erklärt
Unter dem Drehmoment kannst du dir eine Kraft vorstellen, die auf einen drehbar gelagerten Körper wirkt. Deswegen bezeichnest du es auch als Drehkraft. Mit ihr kannst du beispielsweise berechnen, wie fest du eine Schraube ziehen musst, sodass sie nicht zu locker oder fest sitzt und somit einen Maschinendefekt verursacht.
Das Drehmoment mit Formelzeichen M hat als Einheit den Newtonmeter (Nm).
Wie du es berechnest, hängt von der Situation ab und auf welche Weise am Drehpunkt die Kraft ausgeübt wird.
Drehmoment Formel
Die Drehmoment Formel für die Berechnung lautet:
M = r ⋅ F
F ist die einwirkende Kraft in Newton und r die Länge des Hebelarms von der Wirkungslinie der Kraft zum Drehpunkt in Meter.
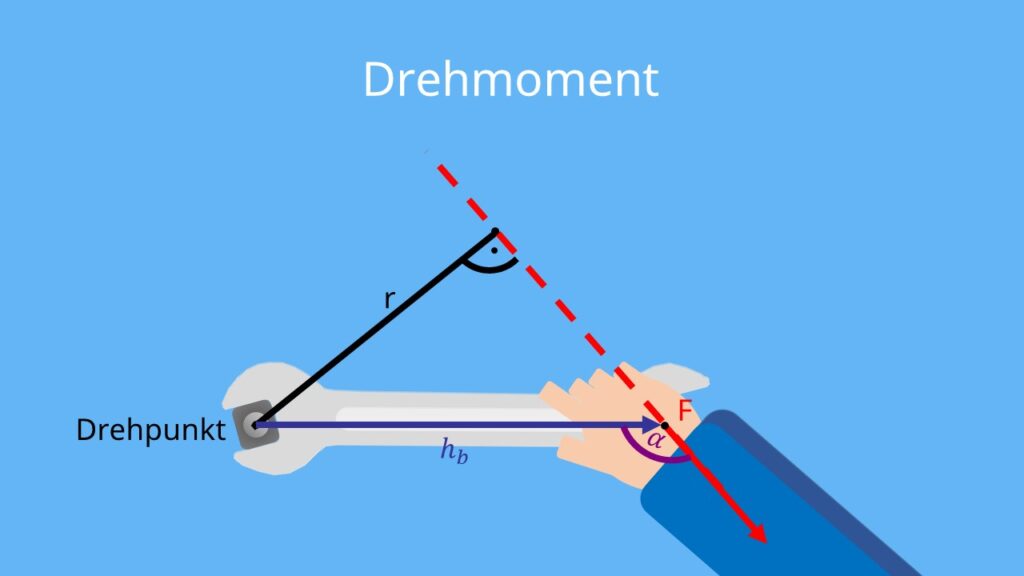
Bei der Formel gehst du davon aus, dass die Kraft genau senkrecht zum Hebelarm wirkt. Das wäre der Fall, wenn der Schraubenschlüssel in der Hebelarm-Linie liegen würde.
Nicht senkrechte Krafteinwirkung
Wenn die Richtung der einwirkenden Kraft nicht genau senkrecht zum Hebelarm wirkt, muss die Formel leicht abgeändert werden. Denn dann wirkt nur ein Teil der Kraft, die du beim Ziehen der Schraube aufwendest, in die Rotation und somit in das Drehmoment.
Dabei ändert sich weder die Richtung noch Stärke, mit der du am Schraubenschlüssel ziehst. Der Abstand zu dem Drehpunkt, also der Hebelarm, verändert sich allerdings.
Ein stumpferer Winkel α zwischen dem Hebel und der Wirkungslinie der Kraft führt zu einem kürzeren Hebelarm und somit zu einem kleineren Drehmoment. Wenn der Winkel sich allerings 90° annähert, wird der Hebelarm länger und das Drehmoment größer.
Die Länge des Hebelarms bestimmst du dann mit folgender Formel:
r = hb⋅ sin(α)
Dementsprechend lautet die abgeänderte Formel dann:
M = hb⋅ sin(α) ⋅ F
Gleichgewicht Drehmoment
Auf drehbar gelagerten Körpern können mehrere Drehmomente gleichzeitig wirken. Das ist zum Beispiel bei Balkenwaagen wichtig. Diese müssen so ausgerichtet sein, dass sie exakt im Gleichgewicht stehen, bevor ein Gewicht auf eine Seite gelegt wird.
Soll sich ein Hebel im Gleichgewicht befinden, muss die Summe aller Drehmomente Null ergeben.
∑ M = 0
Die sich nach links drehenden Drehmomente und die sich rechts drehenden Drehmomenten müssen sich dabei im gesamten Körper ausgleichen.
Welches Vorzeichen hat das Drehmoment?
Wenn du ein Drehmoment für einen Punkt des Körpers berechnest, auf den mehrere Drehmomente wirken, musst du beachten, ob die Drehmomente positiv oder negativ sind.
Dreht sich das Moment gegen den Uhrzeigersinn, ist es positiv. Dreht es sich im Uhrzeigersinn, ist es negativ.
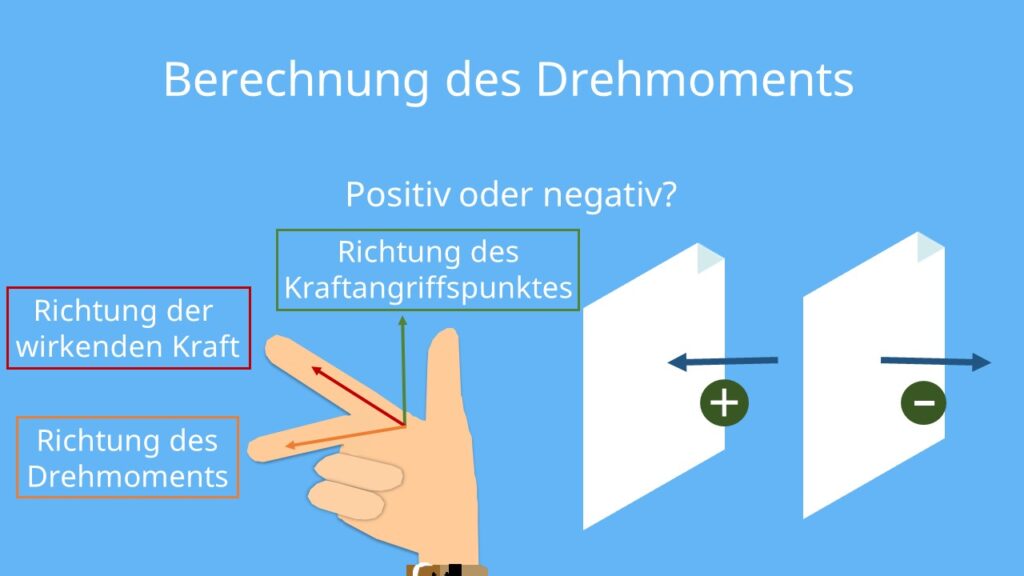
Rechte Hand Regel
Um die Vorzeichen der Momente festzustellen, kannst du auch die Rechte Hand Regel anwenden. Dabei richtest du Daumen, Zeigefinger und Mittelfinger so aus, dass sie zueinander rechtwinklig stehen.
- Der Daumen ist dabei in Richtung des Kraftangriffspunktes gerichtet
- Der Zeigefinger weist in Richtung der wirkenden Kraft
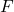
- Der Mittelfinger zeigt nun in Richtung des Drehmoments.
Zeigt der Mittelfinger in das Blatt hinein, ist das Drehmoment positiv. Hierbei ist dein Mittelfinger von dir weg gerichtet. Zeigt er zu dir hin, ist das Drehmoment negativ.
Drehmoment berechnen – Beispiel
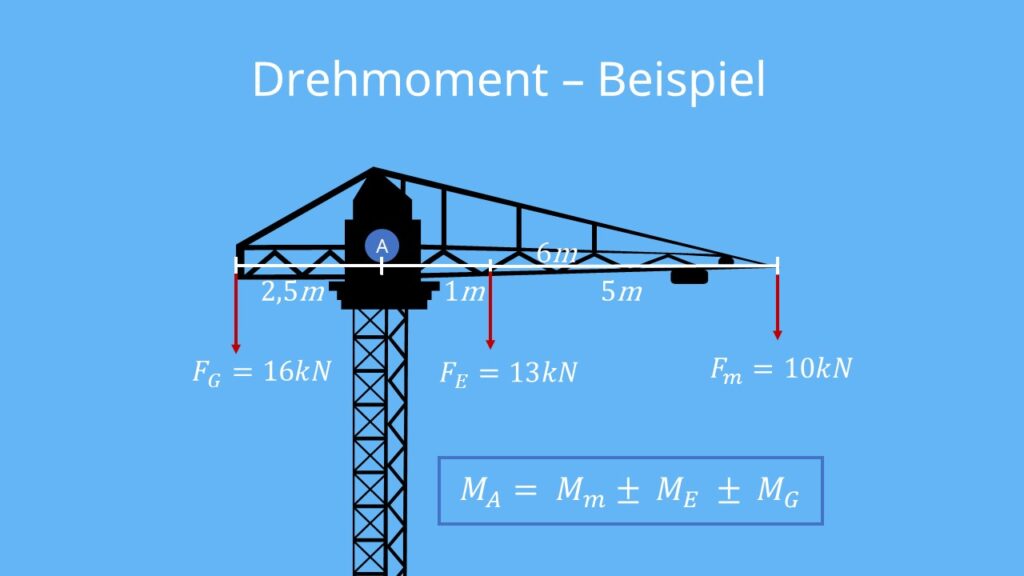
Der Drehkran ist ein typisches Beispiel für einen Körper, bei welchem mehrere Drehmomente auf einen Drehpunkt wirken.
Dieser Drehkran wird mit einer Last Fm von 10 Kilonewton am Kranende belastet. Des Weiteren wirkt sein Eigengewicht FE mit 13 Kilonewton. Diese Belastung liegt 1 Meter rechts neben dem Drehpunkt A.
Sein Gegengewicht FG mit 16 Kilonewton wirkt am kürzeren Ende, 2,5 Meter links neben A. Die Reichweite des Krans beträgt dabei 6 Meter, also die 1 Meter bis zum Belastungspunkt des Eigengewichts und dann noch weitere 5 Meter bis zum Kranende mit der Last.
Berechnung
Für die Berechnung des Drehmoments am Punkt A stellst du alle angreifenden Momente an diesem Punkt fest:
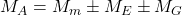
Damit du weißt, welche Momente addiert und welche subtrahiert werden, brauchst du die Vorzeichen der Momente. Hierzu kannst du die Rechte Hand Regel heranziehen.
Im Beispiel von Mm streckst du deinen Daumen nach links aus, da der Drehpunkt und somit die Richtung des Kraftangriffspunktes links von Mm liegen. Dein Zeigefinger richtet sich nach unten, da die Gewichtskraft der Last den Kran nach unten zieht. Nun ist dein Mittelfinger zu dir hin gerichtet. Das Drehmoment Mm ist also negativ.
Wenn du das bei ME und für MG auch anwendest, kommt für ME ein negatives Vorzeichen und für das Moment MG ein positives Vorzeichen heraus.
Jetzt musst du nur noch die Kräfte mit den zugehörigen Hebelarmen einsetzen. Die Hebelarme sind die jeweiligen Abstände zum Drehpunkt A. Du erhältst als Gleichung:
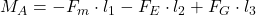
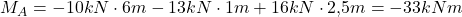
Für das Drehmoment in Punkt A ergibt sich damit minus 33 Kilonewtonmeter! Das kann im Zweifel dazu führen, dass der Kran instabil wird und zu stark in eine Richtung schwenkt. Je nach Aufbau und Material des Krans passiert aber häufig nichts Verheerendes.
Drehmoment Übungsaufgabe
Nun schauen wir uns eine Übungsaufgabe an, um das Drehmoment in einem praktischen Beispiel zu verstehen.
Stell dir vor, du bist gerade dabei, mit einem Bekannten dein Haus zu renovieren. Als Außenbeleuchtung möchtest du über der Balkontür im zweiten Stock noch eine Lampe montieren. Da der Balkon auch noch nicht fertig ist, kommst du auf die Idee, ein Brett zur Balkontür hinauszulegen.
Du hast dafür nur ein Brett mit einer Länge von 5 Meter zur Verfügung. Es ragt dabei 3 Meter über die Balkontür ins Freie hinaus. Damit es nicht kippt, stellt sich dein Bekannter mit einem Gewicht von 90 Kilogramm im Innenraum auf das Brett.
Jetzt stellt sich die Frage: Kannst du mit einem Gewicht von 75 Kilogramm auf das Brett hinauslaufen, ohne dass es kippt? Das Gewicht des Bretts kannst du dabei vernachlässigen.
Die Lösung zu dieser Aufgabe mit einem verständlichen Rechenweg erfährst du in unserem Übungsvideo .
Drehmoment Klausuraufgabe
Die nachfolgende Aufgabe bereitet dich bestens für das Thema Drehmoment in deiner Klausur vor.
Gehen wir einmal davon aus, du bist Archäologe und gerade auf der Suche nach einem wertvollen Schatz. Du hast die Information erhalten, dass der Schatz in einem Schacht versteckt ist. Der Eingang ist dabei mit einem großen Stein geschützt.
Dieser hat eine Würfelform mit der Kantenlänge 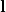 . Als du den Stein findest, befestigst du an der rechten oberen Kante ein Seil und versuchst damit den Stein zu kippen.
. Als du den Stein findest, befestigst du an der rechten oberen Kante ein Seil und versuchst damit den Stein zu kippen.
Mit welcher Kraft musst du mindestens am Seil ziehen, um den Stein kippen zu können? Unter welchem Winkel ist die Kraft minimal?
In unserem Video zur Klausuraufgabe erklären wir dir, wie du diese Aufgabe bearbeiten kannst.
Drehmoment — häufigste Fragen
-
Wofür braucht man das Drehmoment?
Das Drehmoment wird besonders in der Technik und Mechanik gebraucht. Im Automobilbereich ist das Drehmoment beispielsweise ein wichtiger Faktor bei der Auslegung von Motoren und Getrieben. Aber auch im Handwerk wird das Drehmoment gebraucht, um zum Beispiel eine Schraube nicht zu locker oder fest zu drehen.
-
Wie berechnet man das Drehmoment?
Für die Berechnung des Drehmomentes gilt die Formel: M = r⋅F
Also sind folgende Faktoren für die Berechnung wichtig:- Die Richtung der Kraft F (Wirkungslinie)
- Die Höhe der Kraft F (Betrag)
- Die Länge des Hebelarms r
-
Wie berechnet man das Nm (Newtonmeter)?
Newtonmeter ist eine Einheit, die sich aus der Multiplikation von der Krafteinheit Newton und der Längeneinheit Meter zusammensetzt: Newton (N) ⋅ Meter (m) = Newtonmeter (Nm).
Hebelgesetz
Das Drehmoment wird bei Hebeln relevant, auf die Kraft einwirkt. Was das Hebelgesetz damit zu tun hat und welche Arten von Hebeln es gibt, erfährst du hier !