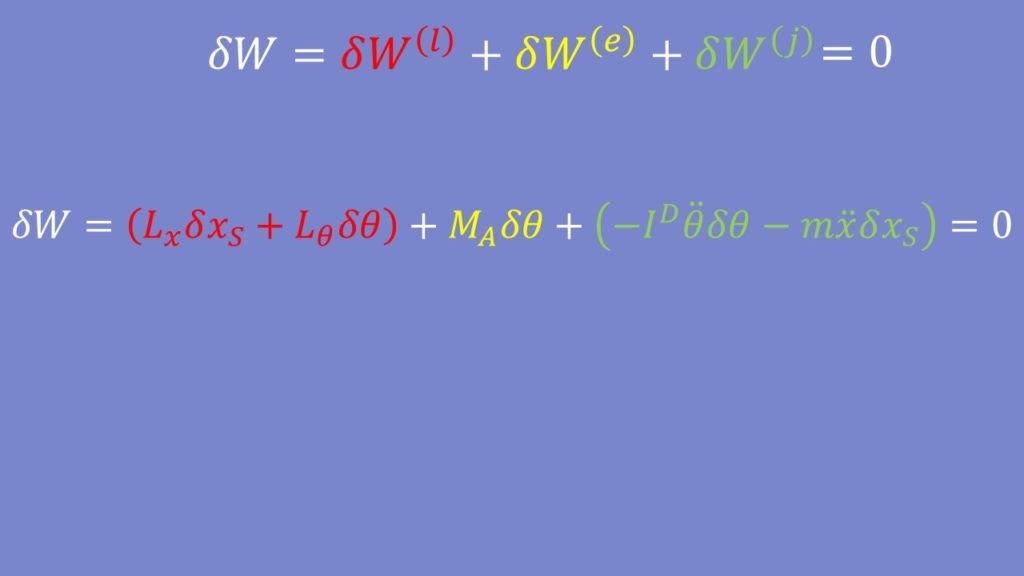Dynamik von starren Körpern – PdvV
Für was steht denn bitte PdvV? Das und vieles mehr erklären wir dir in diesem Beitrag und Video.
Inhaltsübersicht
Das Prinzip der virtuellen Verrückung
Zu Beginn fassen wir nochmal zusammen, was du über die Dynamik von Starrkörpersystemen wissen solltest: Starrkörpersysteme sind Systeme, die aus mehreren Starrkörpern bestehen und dadurch komplex zu berechnen sind. Dementsprechend gibt es zwei Wege, die Bewegungsgleichungen in Form von Differenzialgleichungen zu bestimmen: Das Prinzip der virtuellen Verrückung und die Lagrange’schen Gleichungen. Für diese Wege wird das System vorher parametrisiert und anschließend so viele Differentialgleichungen, wie es Parameter gibt, bestimmt. Jetzt betrachten wir nur das Prinzip der virtuellen Verrückung, das wir schon im Video dazu näher erklärt haben. Die Lagrange’schen Gleichungen schauen wir uns dann im nächsten Video genauer an.
Schreibweise des PdvV
Allgemein schreiben wir das PdvV als:
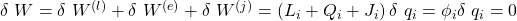
Li, Qi und Ji fassen die Arbeit verursachenden Kraftgrößen zusammen. Dabei gilt als Faustregel: Wenn qi ein Winkel ist, ist die Kraftgröße ein Moment. Wenn qi eine Weg-Größe ist, ist die Kraftgröße eine Kraft.
Jetzt haben wir die Grundlagen wiederaufgefrischt. Als Beispiel betrachten wir nun einen rollenden Reifen als ebenes Problem. Dabei wird die Bewegung durch ein äußeres Moment MA=5Nm verursacht. Der Reifen selbst hat die Masse m=10kg und den Radius R=0,5m. Er befindet sich logischerweise im Erdschwerefeld und bewegt sich auf einer ebenen Fläche mit einem Reibkoeffizienten 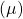 gleich 0,8. Ziel ist es jetzt die DGL der Bewegung zu bestimmen.
gleich 0,8. Ziel ist es jetzt die DGL der Bewegung zu bestimmen.
Dafür müssen wir das System als erstes parametrisieren. Der Reifen hat zwei Freiheitsgrade: die Bewegung parallel zur Ebene und die Kreisbewegung. Für die Kreis- bzw. Rollbewegung bietet sich ein Winkel Theta an. Dieser beschreibt, um wie viel Grad sich der Reifen schon gedreht hat. Dementsprechend ist der Winkel bei einer vollen Umdrehung 360 Grad. Für die Bewegung parallel zum Boden, bietet sich die Schwerpunktkoordinate xS an. Wir haben also die zwei Parameter:
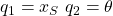
Zusammensetzten der Teilarbeiten
Als nächstes betrachten wir die Teilarbeiten Delta W L, Delta W E und Delta W J, aus denen sich die gesamte Arbeit zusammensetzt, separat. Dabei müssen wir nur die Kraftgrößen betrachten, die durch eine Verrückung unserer Parameter Arbeit verursachen. Wir beginnen mit der Arbeit durch äußere Kräfte: 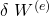 . Als äußere Kraftgröße haben wir hier lediglich das angreifende Moment, das Arbeit verursacht, da die Wirkrichtung der Gewichtskraft in y-Richtung ist und die Parameter in y-Richtung keine Arbeit verursachen. Wir erhalten also:
. Als äußere Kraftgröße haben wir hier lediglich das angreifende Moment, das Arbeit verursacht, da die Wirkrichtung der Gewichtskraft in y-Richtung ist und die Parameter in y-Richtung keine Arbeit verursachen. Wir erhalten also:
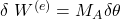
Als nächstes betrachten wir die Arbeit, die durch Bindungen verursacht wird. Dabei ist die einzige „Bindung“ der Kontakt zum Boden. Hier haben wir die Reibkraft Lx und das Rollwiderstandsmoment LTheta. Demensprechend erhalten wir:
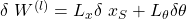
LTheta resultiert aus der unsymmetrischen Verformung des Reifens am Boden. In unserem Fall beträgt das Rollwiderstandsmoment LTheta 1Nm. Die Reibkraft können wir wiederrum mit Hilfe der Normalkraft N und dem Reibkoeffizienten berechnen. Die Normalkraft erhalten wir aus einem Kräftegleichgewicht in y-Richtung. Das Gleichgewicht können wir bilden, da wir keine Bewegung in y-Richtung haben. Somit erhalten wir, dass die Normalkraft gleich der Gewichtskraft sein muss. Es ergibt sich für die Reibkraft:
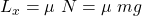
Verursachte Arbeit
Zum Schluss betrachten wir noch die Arbeit, die durch Beschleunigungen verursacht wird. Hier haben wir zum einen eine Kraft FH in x-Richtung aber auch ein Moment MH in Folge der Massenträgheit bzw. des Massenträgheitsmoments. Falls du dazu noch Fragen hast, dann schau dir am besten nochmal das Video Drallsatz I an.
Wir erhalten dann für die Arbeit durch Beschleunigungen:
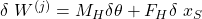
FH bildet die d’Alembertsche Hilfskraft und MH folgt aus dem Drallsatz bezogen auf den Berührpunkt D von Rad und Boden. Wir erhalten somit:
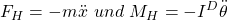
Mit
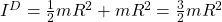
Das negative Vorzeichen kommt aus der Wahl der Bewegungsrichtung, also in unserem Fall in negative x-Richtung.
Schreiben wir nun die gesamte Arbeit auf, erhalten wir:
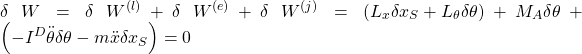
Anschließend sortieren wir die Gleichung nach unseren Parametern
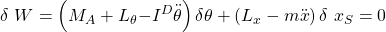
Um die Gleichung zu erfüllen, müssen beide Klammern gleich 0 sein und wir erhalten zwei Differenzialgleichungen – bezüglich jedes Parameters eine:
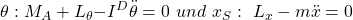
Setzen wir nun unsere Werte ein, erhalten wir:
Damit haben wir die Differentialgleichungen aufgestellt und die Aufgabe gelöst.
So, jetzt weißt du wie die Arbeit mit dem Prinzip der virtuellen Verrückung zusammenhängt. Mach’s gut und bis bald!