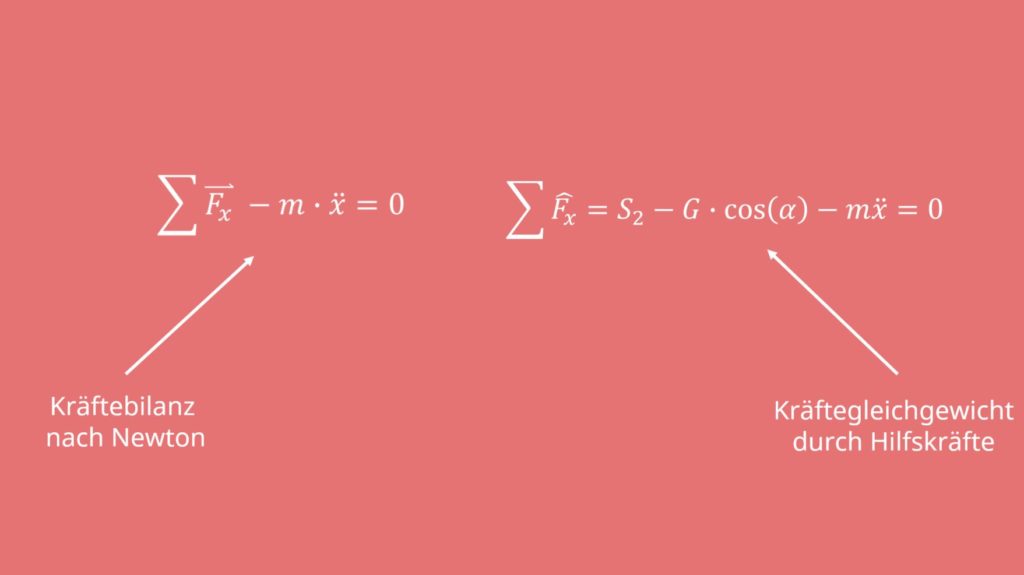d’Alembert
D’Alembert war ein bedeutender Mathematiker und Physiker im 18. Jahrhundert. Zu beiden Wissenschaftsgebieten hat er wichtige Forschungsbeiträge verfasst. Beispielsweise wurde in der Mechanik das d’Alembertsche Prinzip nach ihm benannt. Dieses erlaubt uns Gleichungen für Bewegungen mit bestimmten Bedingungen aufzustellen. In unserem Video erklären wir dir in kürzester Zeit dieses Prinzip. Schau doch mal rein!
Am Anfang solltest du wissen, dass wir uns wir uns beim dynamischen Gleichgewicht nach d’Alembert nicht mehr in der Kinematik, sondern in der Kinetik des Massenpunktes befinden. Grundlage für dieses Themengebiet sind die drei Newtonschen Axiome . Wir betrachten also nicht mehr nur noch die Bewegung an sich, sondern auch deren Ursachen, beispielsweise die Kräfte.
Inhaltsübersicht
D’Alembertsches Prinzip
Das d’Alembertsche Prinzip ist eine Erweiterung des Prinzips der virtuellen Arbeit auf die Dynamik. Das Prinzip von d’Alembert besagt, dass eine Bewegung eines Objektes so stattfindet, dass die virtuelle Leistung der Zwangskräfte zu jedem Zeitpunkt null wird. Eine Zwangskraft ist dabei diejenige Kraft, die einen Körper durch vorgegebene Zwangsbedingungen in seiner Bewegungsfreiheit einschränkt.
Mit anderen Worten ist die Summe aller an einem Körper angreifenden Kräfte plus die d’Alembertsche Trägheitskraft für diesen null und das Objekt befindet sich in einer Gleichgewichtslage. Diese Lage ist genauer betrachtet eine dynamische. Die Trägheitskraft ist dabei eine d’Alembertsche Hilfskraft, um diese Gleichgewichtslage herzustellen.
Was heißt jetzt nun dynamisches Gleichgewicht? Dazu erinnern wir uns zurück an die Statik: Gleichgewicht ist der Zustand eines Körpers, indem sich die einander entgegengesetzt wirkenden Kräfte aufheben. Dasselbe gilt auch bei dem dynamischen Gleichgewicht, nur, dass dieses immer in Bewegung ist.
Beispiel Kugel im freien Fall mit Trägheitskraft
Eine Kugel mit der Masse 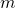 erfährt im freien Fall die Erdbeschleunigung
erfährt im freien Fall die Erdbeschleunigung 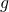 . Damit wirkt auf den Körper die Gewichtskraft
. Damit wirkt auf den Körper die Gewichtskraft 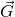 :
:
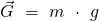
Dieser Zusammenhang gilt aber nur für die Beobachtung aus einem ruhenden Inertialsystem heraus. Erfährt der Beobachter dieselbe Beschleunigung und befindet sich stets neben dem Körper, wird von einem mit beschleunigten System (kein Inertialsystem) gesprochen. Aus dieser Beobachtungsperspektive ruht die Kugel.
Damit sich die Kugel in diesem System aber in Ruhe befinden kann, muss eine der Gewichtskraft der Kugel entgegengesetzte Kraft auf die Kugel wirken, denn die Summe aller Kräfte ist im Gleichgewicht gleich null. Diese entgegenwirkende Kraft wird Trägheitskraft genannt und ist hier mit 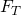 und der Beschleunigung
und der Beschleunigung  symbolisiert:
symbolisiert:
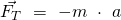
Zusammenfassend bedeutet das, dass auf einen Körper in einem mit beschleunigten System, neben einer beschleunigenden Kraft 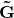 auch eine entgegengesetzte Trägheitskraft wirkt. Somit befindet sich die Kugel für den Beobachter im beschleunigten System in Ruhe, da die Summe aller Kräfte auf die Kugel gleich null ist. In allgemeiner Form sieht das dann so aus:
auch eine entgegengesetzte Trägheitskraft wirkt. Somit befindet sich die Kugel für den Beobachter im beschleunigten System in Ruhe, da die Summe aller Kräfte auf die Kugel gleich null ist. In allgemeiner Form sieht das dann so aus:
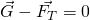
mit 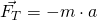
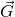 –
– 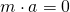
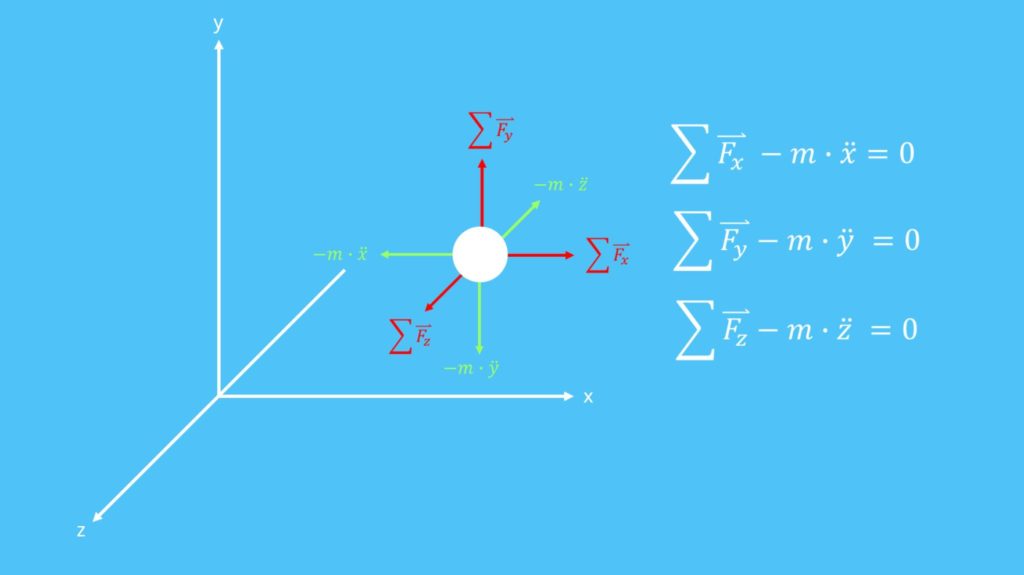
Komponentendarstellung von Hilfskräften
Treten Kräfte in x-, y- und z- Richtung auf, muss es je nach Koordinatenachse eine Hilfskraft geben, um das Gleichgewicht herzustellen. Dazu werden als erstes alle Beschleunigungen und Geschwindigkeiten und damit alle Kräfte in die jeweilige positive Koordinatenrichtung eingetragen. Danach, entgegengesetzt dazu, die entsprechenden Hilfskräfte. So erhalten wir folgende drei Gleichungen in Komponentendarstellung:
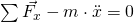
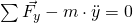
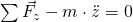
Die zweite zeitliche Ableitung der jeweiligen Koordinatenrichtung ergibt die Beschleunigung. Damit wird eine Kraft von einer entgegengesetzten Kraft subtrahiert. Das Ergebnis muss aufgrund der Gleichgewichtslage im mitbeschleunigten Inertialsystem gleich null sein.
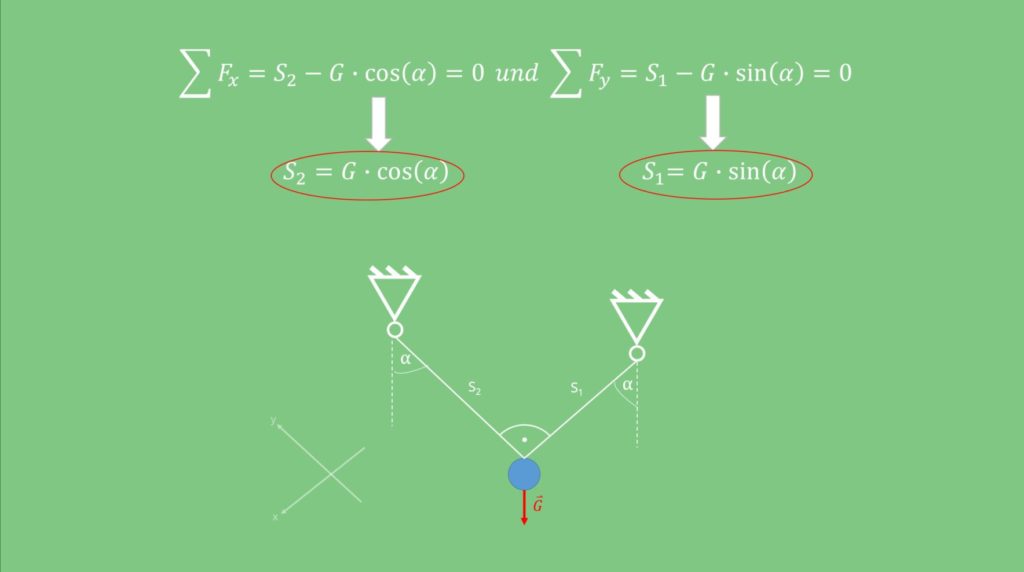
Seilkräfte berechnen
Als zweites wird eine Masse betrachtet, die durch zwei Seile festgehalten wird. Diese sind wiederum mit zwei Festlagern verbunden. Das Koordinatensystem wird nun so gelegt, dass die y-Achse in Richtung Seil 1 zeigt und die x-Achse entgegen Seil 2. Aus der Statik können wir dann ganz einfach das Gleichgewicht bilden:
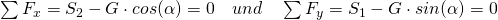
Die Seilkräfte sind dann:
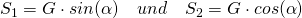
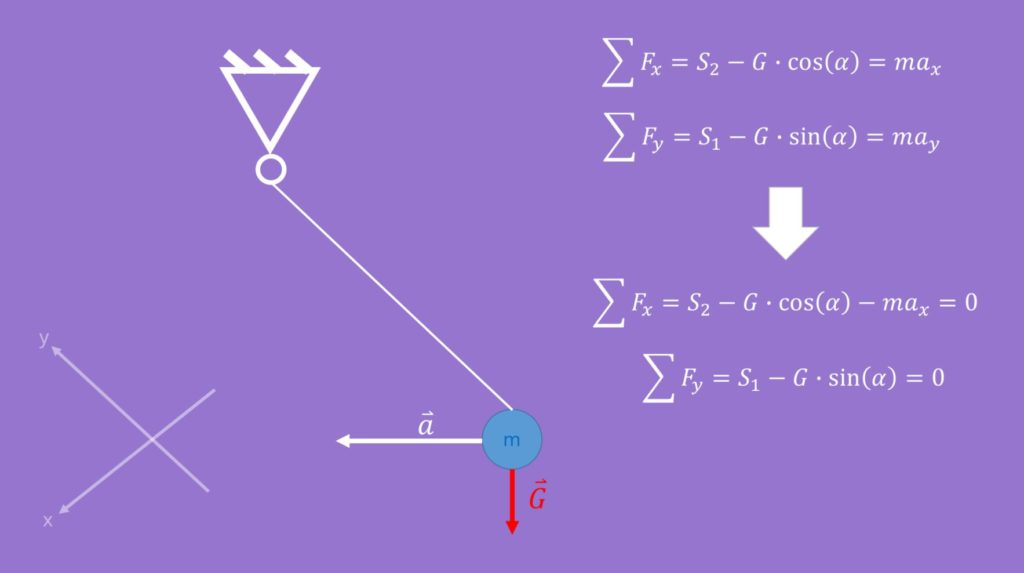
Nun wird das Seil 2 durchgeschnitten. Dadurch kommt es zu einer Bewegung, da das Gleichgewicht gestört wurde. Diese beginnt mit einer Beschleunigung. Durch Newton ist festgelegt, dass die Summe aller Kräfte in diesem Fall nicht Null ist, sondern durch die Masse mal ihrer Beschleunigung gegeben ist. Das ist der Grund, weshalb es zu zwei neuen Gleichungen für die Summe aller Kräfte in x- und y- Richtung
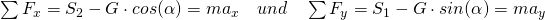
Zum Zeitpunkt des Durchschneidens gibt es keine Beschleunigung in y-Richtung. Dadurch kann 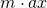 auf die linke Seite gebracht werden.
auf die linke Seite gebracht werden.
So erhalten wir folgende Gleichungen für das dynamische Gleichgewicht:
Kräftegleichgewicht
Wenn du in erstgenannter Gleichung 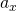 durch
durch 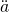 ersetzt, erhältst du wieder die vorherige Gleichung:
ersetzt, erhältst du wieder die vorherige Gleichung:
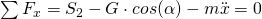
Aber Achtung! Die beiden Gleichungen sind nicht die gleichen. Bei der ersten wurde die Kräftebilanz nach Newton aufgestellt. Bei der zweiten Gleichung wurde die Summe über die angreifenden Kräfte gebildet und dann eine Hilfskraft hinzugenommen, um ein Gleichgewicht zu bilden.
In der Anwendung musst du da jedoch keinen Unterschied machen.
Mit der Hilfe des Prinzips von d’Alembert kannst du ein dynamisches Problem geschickt lösen, denn durch die Hilfskräfte wird diese Art des Problems auf ein statisches Problem übertragen. Das Prinzip von d’Alembert fordert ein Gleichgewicht aller Zwangskräfte. Laut dem Prinzip der virtuellen Arbeit, verrichten diese Kräfte bei einer virtuellen Verrückung keine Arbeit, wenn ein Gleichgewichtsfall vorliegt. Daraus folgt dann das d’Alembertsche Prinzip.