Impulserhaltungssatz
Der Impulserhaltungssatz ist einer der wichtigsten Erhaltungssätze in der Physik. Er kann in der klassischen Mechanik, Quantenmechanik und der speziellen Relativitätstheorie angewandt werden. Wenn du genau wissen willst, was die Impulserhaltung ausmacht und wie sie angewandt wird, dann schau dir doch unser Video dazu an. Dort erklären wir dir das alles in kürzester Zeit!
Inhaltsübersicht
Impuls Physik
Der Impuls ist definiert als:

Dabei bezeichnet 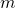 die Masse und
die Masse und 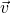 die Geschwindigkeit des beobachteten Objekts. Die Masse
die Geschwindigkeit des beobachteten Objekts. Die Masse 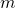 ist eine skalare Größe.
ist eine skalare Größe. 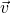 und
und 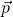 sind Vektoren, die in dieselbe Richtung zeigen. Somit ist die Bewegungsrichtung gleich der Impulsrichtung. Je schwerer und schneller nun der beobachtete Körper ist, desto größer ist auch sein Impuls.
sind Vektoren, die in dieselbe Richtung zeigen. Somit ist die Bewegungsrichtung gleich der Impulsrichtung. Je schwerer und schneller nun der beobachtete Körper ist, desto größer ist auch sein Impuls.
Wenn der Impuls eines Körpers verändert wird, so verändert sich die Geschwindigkeit von diesem mit. Die Veränderung des Impulses für eine bestimmte Zeit entspricht somit der Kraft 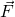 .
.
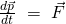
Impuls Einheit
In diesem Kapitel wird die Einheit des Impulses hergeleitet. Dafür wird ein Körper definiert, der eine Masse von 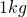 und eine Geschwindigkeit von
und eine Geschwindigkeit von 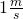 besitzt. Dies wird in die Formel des Impulses eingesetzt und ergibt:
besitzt. Dies wird in die Formel des Impulses eingesetzt und ergibt:
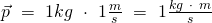
Das erinnert sehr stark an die Einheit der Kraft, welche als Newton [N] definiert ist.
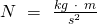
So kann der obige Zusammenhang verändert werden, sodass sich die Einheit des Impulses ergibt:
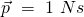
Impulserhaltung
Der Impulserhaltungssatz wird aus dem zweiten und dritten Newtonschen Axiom abgeleitet. Wenn keine Kraft auf eine betrachtete Masse wirkt, so muss die Ableitung des Impulses null sein. Daraus folgt, dass der Impuls konstant sein muss. Anders formuliert ergibt sich der Impulserhaltungssatz: Die Änderung des Impulses in einem kräftemäßig abgeschlossenen System ist gleich null.
Dabei ist es egal, ob ein Massepunkt oder ein System von Massenpunkten betrachtet wird. Dieser Zusammenhang gilt immer. Als ein kräftemäßig abgeschlossenes System wird ein System bezeichnet, auf das keine Kraft von außen wirkt, die den Impuls verändern könnte.
Schwerpunktsatz
Die Tatsache, dass es keine Rolle spielt, ob ein Massepunkt oder ein Massepunktsystem betrachtet wird, beruht auf dem Schwerpunktsatz. Dieser besagt, dass sich der Massenschwerpunkt eines Systems genauso bewegt, als wären alle Massenpunkte in ihm vereinigt und alle äußeren Kräfte wirken nur auf ihn.
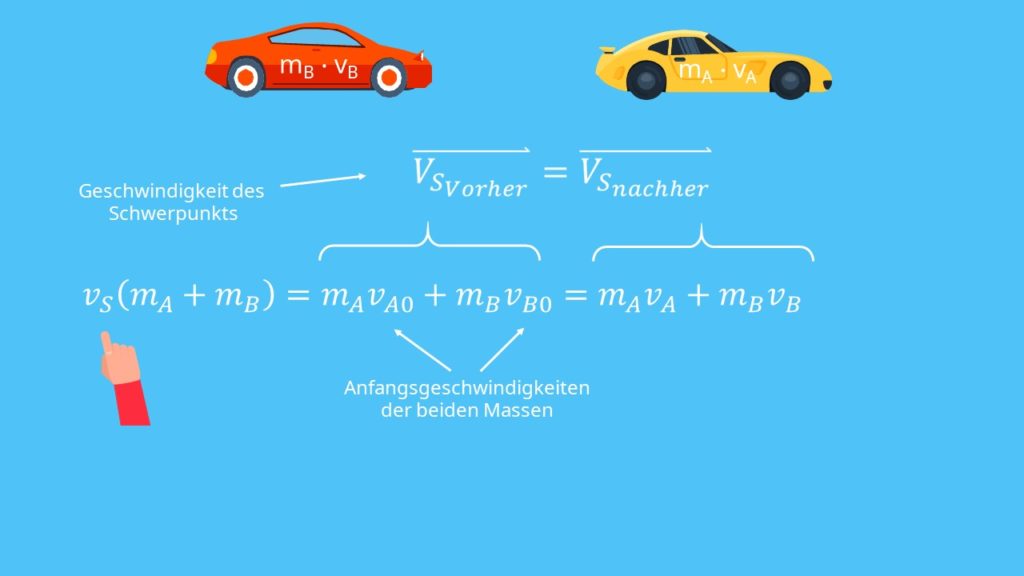
Impulserhaltungssatz Formel
Der Impulserhaltungssatz kann bei dem Zusammentreffen zweier Körper mit unterschiedlichen Massen 1 und 2 verdeutlicht werden. Es wirkt keine äußere Kraft. Damit handelt sich um ein kraftmäßig abgeschlossenes System. Prallen die zwei Objekte aufeinander, entsteht nach dem dritten Newtonschen Axiom eine Kraft von Körper 1 auf den zweiten 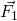 und von Körper 2 eine auf den ersten
und von Körper 2 eine auf den ersten 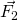 . Diese sind einander entgegengesetzt:
. Diese sind einander entgegengesetzt:
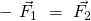
Da die Kraft als Masse 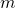 mal die Beschleunigung
mal die Beschleunigung  definiert ist, lässt sich schreiben:
definiert ist, lässt sich schreiben:
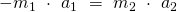
Die Beschleunigung ist eine Veränderung der Geschwindigkeit über einen Zeitraum 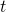 hinweg:
hinweg:
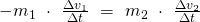
Jetzt kann mit 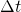 multipliziert werden. Daraufhin werden noch die Anfangs- und Endgeschwindigkeiten (
multipliziert werden. Daraufhin werden noch die Anfangs- und Endgeschwindigkeiten (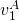 und
und 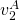 ) eingeführt, um das Delta aufzulösen.
) eingeführt, um das Delta aufzulösen.
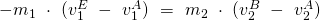
Zum Schluss werden alle Variablen vor dem Stoß auf die linke und alle Variablen für nach dem Stoß auf die rechte Seite gebracht. Das ergibt:
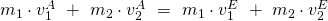
Da 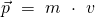 kann die Formel noch vereinfacht werden:
kann die Formel noch vereinfacht werden:
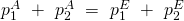
An der Gleichung kann festgestellt werden, dass der Impuls vor der Wechselwirkung der zwei Körper gleich dem Impuls nach der Wechselwirkung dieser ist. Das ist der Impulserhaltungssatz.
Zentraler gerader Stoß
Der zentrale gerade Stoß ist ein Fall, bei dem der Impulserhaltungssatz angewandt werden kann. Es stoßen zwei Körper 1 und 2 gerade aufeinander. Dabei handelt es sich um ein gegen Kräfte abgeschlossenes System. Die Impulserhaltung lässt sich dann wie im vorigen Kapitel herleiten und bestimmen.
Des Weiteren kann von jedem Stoß die Stoßzahl  bestimmt werden. Die Kennzahl wird auch Restitutionskoeffizient genannt. Die Formel setzt sich aus den jeweiligen Geschwindigkeiten vor und nach der Wechselwirkung durch den Zusammenstoß der Körper zusammen.
bestimmt werden. Die Kennzahl wird auch Restitutionskoeffizient genannt. Die Formel setzt sich aus den jeweiligen Geschwindigkeiten vor und nach der Wechselwirkung durch den Zusammenstoß der Körper zusammen.
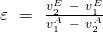
Dabei gilt, dass Stöße, die durch ein 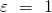 gekennzeichnet sind, elastisch
verlaufen. Bei einem Restitutionskoeffizient von 0 hingegen ist der Zusammenstoß rein plastisch oder auch unelastisch
. Der Koeffizient selbst ist dabei materialabhängig und wird durch Versuche empirisch ermittelt.
gekennzeichnet sind, elastisch
verlaufen. Bei einem Restitutionskoeffizient von 0 hingegen ist der Zusammenstoß rein plastisch oder auch unelastisch
. Der Koeffizient selbst ist dabei materialabhängig und wird durch Versuche empirisch ermittelt.
Drehimpuls
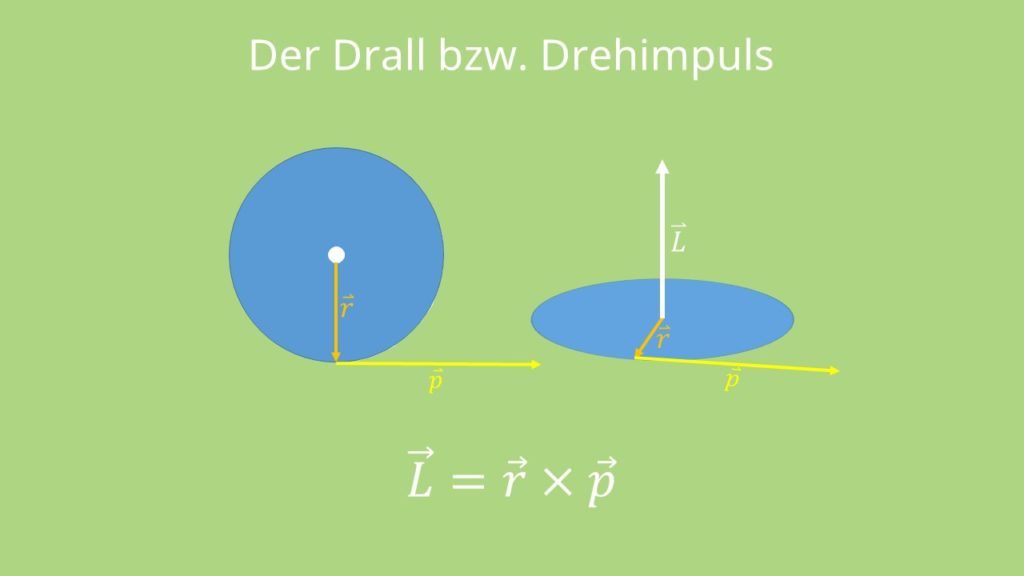
Der Impuls und der Impulserhaltungssatz können beide auch auf Rotationsbewegungen angewandt werden. Ein System hat beispielsweise einen Drehimpuls, wenn es sich um einen Schwerpunkt dreht. Der Drehimpuls ist durch folgendes Vektorprodukt definiert:
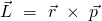
Der Ortsvektor ist dabei 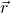 und
und 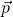 ist der Impuls des beobachteten Körpers.
ist der Impuls des beobachteten Körpers.
Wird der Drehimpuls nach der Zeit abgeleitet, ergibt sich das Drehmoment M, was auch so im Drallsatz festgehalten ist:
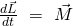
Falls du mehr zu dem Drehimpuls wissen möchtest, haben wir dir hier einen extra Beitrag verlinkt.