Kinematik des starren Körpers II
Du weißt jetzt schon was die Kinematik des starren Körpers ist, aber willst noch ein bisschen Üben? Hier bist du richtig!
Inhaltsübersicht
Übung und Beispiele für die Berechnung der Kinematik
Zu Beginn machen wir nochmal eine kurze Zusammenfassung: Unser Ziel ist es, die Bewegung des starren Körpers zu beschreiben. Dazu brauchen wir den Ort, die Geschwindigkeit und die Beschleunigung. Den Ort beschreiben wir durch eine einfache vektorielle Darstellung. Die Geschwindigkeit eines Punktes A kann mit Hilfe eines weiteren Punktes B dargestellt werden:
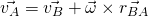
Omega beschreibt dabei die ortsfeste Winkelgeschwindigkeit und r BA den Vektor von B nach A. Eine weitere Möglichkeit die Geschwindigkeit zu bestimmen ist es den Abstand eines Punktes zum Ursprung zu betrachten. Dazu darf die Bewegung von keiner weiteren Bewegung abhängig sein. Beschrieben wird das durch:
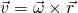
Dabei sind beide Formeln grundsätzlich äquivalent zu einander und je nach System bietet sich eine der beiden Formeln mehr an.\bigmDie Beschleunigung wiederrum kann durch einen zweiten Punkt dargestellt werden:
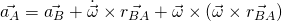
Hier ist Omega punkt die sogenannte Winkelbeschleunigung.
Beispiel – Bewegung des Rades um zwei Achsen
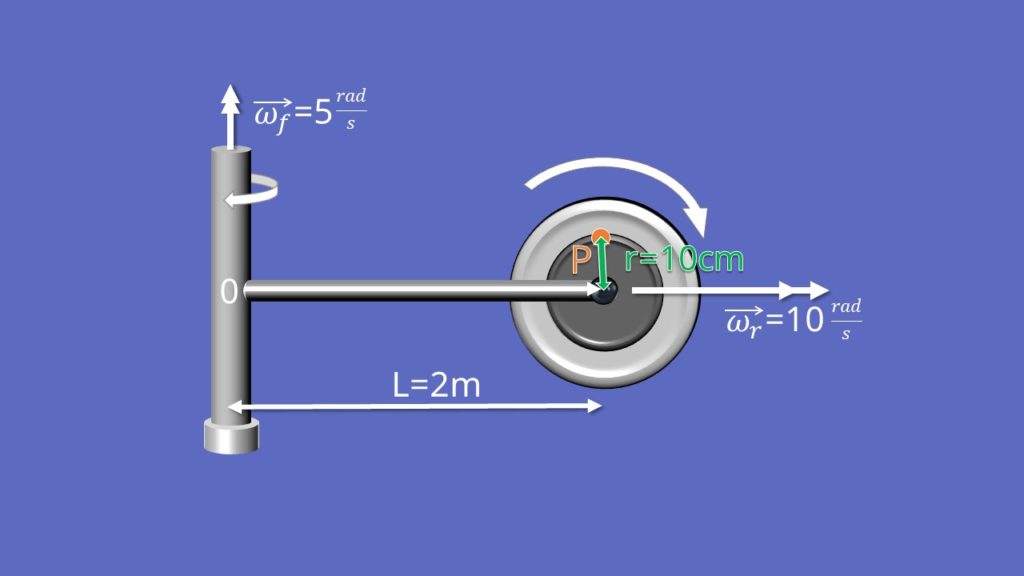
Nachdem wir die Grundlagen geklärt haben, betrachten wir das erste Beispiel: Die Bewegung eines Rades um zwei Achsen. Das Rad selbst hat eine konstante Winkelgeschwindigkeit 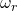 =10 Rad pro Sekunde
=10 Rad pro Sekunde
Es ist genau im Zentrum durch einen Stab der Länge L=2 Meter mit einer senkrechten Stange verbunden, die die konstante Winkelgeschwindigkeit 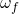 =5 Rad pro Sekunde hat. Nun interessiert uns welche Geschwindigkeit an dem Punkt P herrscht, der einen Abstand von r=10 cm zur Radmitte hat.
=5 Rad pro Sekunde hat. Nun interessiert uns welche Geschwindigkeit an dem Punkt P herrscht, der einen Abstand von r=10 cm zur Radmitte hat.
Zu Beginn setzen wir nun den Ursprung genau in dem Punkt, wo der Stab mit der Stange verbunden ist. Die x-Achse zeigt immer durch den Stab hindurch auf das Rad. Als nächstes schauen wir uns die Formel für die Geschwindigkeit an:
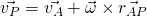
Der Punkt A liegt in diesem Fall genau im Zentrum der Scheibe. Damit erhalten wir:
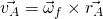
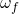 ist uns ja bekannt.
ist uns ja bekannt. 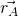 ist unsere Länge L. Setzen wir das ganze nun ein, erhalten wir für die Geschwindigkeit in A:
ist unsere Länge L. Setzen wir das ganze nun ein, erhalten wir für die Geschwindigkeit in A:
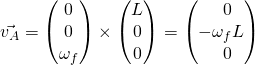
Nun ist die Frage: welches Omega verwenden wir für die Relativgeschwindigkeit? In dem Fall haben wir A so geschickt platziert, dass wir 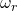 einsetzen können. Denn wir haben nur noch einen Abstand in Richtung von
einsetzen können. Denn wir haben nur noch einen Abstand in Richtung von 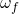 . Das Kreuzprodukt wird dann Null. Somit erhalten wir:
. Das Kreuzprodukt wird dann Null. Somit erhalten wir:
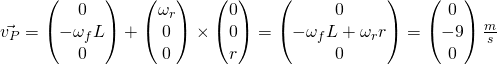
Somit herrscht in Punkt P nur eine Geschwindigkeit in negative y-Richtung mit dem Betrag 9 Meter pro Sekunde.
Beispiel Radiallager
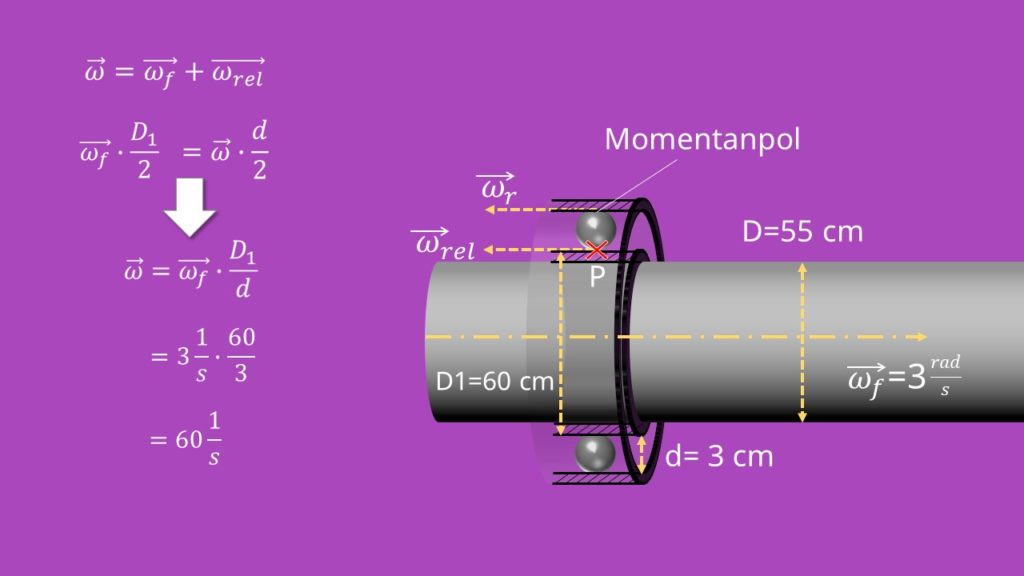
Schauen wir uns gleich noch ein Beispiel, nämlich ein Radiallager an. In diesem befinden sich Kugeln. Solche sogenannten Kugellager werden vergleichsweise häufig verwendet. Wir wollen jetzt herausfinden, welche Winkelgeschwindigkeit die einzelnen Kugeln haben. Dazu betrachten wir eine Welle mit dem Durchmesser D=55 cm, ein Lager mit einem Innenringdurchmesser von D1=60cm und Kugeln mit einem Durchmesser von d=3cm. Die Welle selbst dreht sich mit der konstanten Winkelgeschwindigkeit 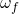 =3 Rad pro Sekunde.
=3 Rad pro Sekunde.
Zu Beginn zeichnen wir uns die Orte und Richtungen der Winkelgeschwindigkeit der Welle 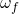 , die Winkelgeschwindigkeit der Kugel relativ zur Welle
, die Winkelgeschwindigkeit der Kugel relativ zur Welle 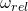 und die absolute Winkelgeschwindigkeit der Kugel Omega ein.
und die absolute Winkelgeschwindigkeit der Kugel Omega ein. 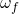 geht genau durch die Mitte der Welle,
geht genau durch die Mitte der Welle, 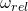 liegt genau am Berührpunkt der Kugel mit dem Innenring, da sich dort die Verbindung der Kugel zur Welle befindet. Omega liegt an dem Punkt, an dem die Kugel den Außenring berührt. Denn dort befindet sich auch unser Momentanpol.
liegt genau am Berührpunkt der Kugel mit dem Innenring, da sich dort die Verbindung der Kugel zur Welle befindet. Omega liegt an dem Punkt, an dem die Kugel den Außenring berührt. Denn dort befindet sich auch unser Momentanpol.
Als nächstes können wir festlegen, dass auch bei der Winkelgeschwindigkeit die Vektoraddition so möglich ist, dass wir diese durch eine absolute und eine relative Winkelgeschwindigkeit ausdrücken können:
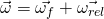
Dadurch, dass 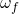 und
und 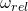 parallel sind, müssen wir die Aufgabe etwas anders lösen. Wir überlegen uns, dass an einem Berührpunkt P der Kugel des Innenrings, und somit indirekt mit der Welle, nur eine Geschwindigkeit herrschen kann. Diese kann man dann über
parallel sind, müssen wir die Aufgabe etwas anders lösen. Wir überlegen uns, dass an einem Berührpunkt P der Kugel des Innenrings, und somit indirekt mit der Welle, nur eine Geschwindigkeit herrschen kann. Diese kann man dann über 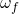 oder über Omega bestimmen. Wir erhalten also zwei Gleichungen:
oder über Omega bestimmen. Wir erhalten also zwei Gleichungen:
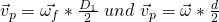
Die Gleichungen können wir jetzt gleichsetzen und nach Omega umformen:
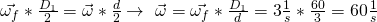
Du erkennst also, dass die Winkelgeschwindigkeit der einzelnen Kugeln immer kleiner wird, je größer die Kugeln selbst werden.
Du siehst: Mit etwas Übung bist du auch zum Thema Kinematik des starren Körpers bald ein Profi.